Сейчас уже общепринято (см., например, [1]), что информационные и информационно-измерительные системы относятся к классу коммуникационных систем.
Обобщенное понятие «ресурса» коммуникационной системы впервые было введено Л.И. Розоноэром [2]. В этой работе обмен и распределение ресурса в системе рассматривались как происходящие по законам, аналогичным закону распределения энергии в замкнутой системе механических частиц. Позже понятие «ресурса» коммуникационной системы стали связывать с наличием некоторого множества коммуникаций, соединяющих элементы системы, и с характеристиками этих коммуникаций.
Мы будем называть прогнозными ресурсами ИИС ее «истинное» значение определяющего параметра, в отличие от «ресурсов потребления» или фактических ресурсов, которые сложились при функционировании системы на данный период (или момент) времени. В связи с этим мы введем понятие «концентрации» основной характеристики системы, понимая под этим термином величину этой характеристики в единице «объема» системы. «Объем» системы определяется для конкретной системы (общее количество каналов связи и т.д.).
Если исходить из представлений классической термодинамики, то можно ввести понятие «энергии образования» коммуникационной системы в результате термодинамического цикла (например, цикла Карно), подобно тому, как это сделано в работе Н.И. Сафронова и др. [3].
Тогда формула для определения затрат энергии на термодинамический цикл образования системы будет иметь вид:
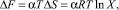(1)
где X = C/C0 (для прямого цикла) и X = C/C0 (для обратного цикла); α – число элементов, вовлеченных в процесс образования системы; R – универсальная газовая постоянная; C0 – начальная и С – конечная концентрации основной характеристики.
Концентрацию основной характеристики сложной системы выразим через равновесную концентрацию Cp. Этот параметр пропорционален к.п.д. цикла, так что полная энергия имеет вид:
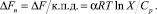(2)
Для прямого и обратного цикла
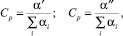(3)
где α′, α″ – количество элементов, вовлеченных в процесс образования системы в прямом и обратном циклах, соответственно;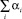 
– общее число элементов, вовлеченных в образование системы. Очевидно, что в прямом цикле α = α′X и в обратном = α = α″X . Подставляя α и Cp в (2), имеем:
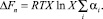(4)
Не меняя общности рассуждений, положим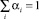 
, тогда получим
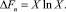(5)
Если дифференцированные ресурсы системы в единице «объема» обозначить через Wx, то
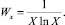(6)
В работе [4] мы применили методы неравновесной термодинамики к ИИС и получили выражение для функции отклика этой системы на внешнее воздействие с учетом диссипативных процессов. После линеаризации полученного нами выражения, функция отклика Ф системы имеет вид:
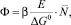(7)
где Е – «емкость» канала связи в системе;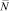 
– среднее число каналов в системе; ΔG0 – энергия Гиббса термостата (внешней среды); β – некоторая постоянная теории, величина которой вычисляется для каждой конкретной системы.
Для идеальных процессов ΔG0 = ΔFп и, с учетом (4), (5) и (6), получим
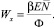(8)
Если «объем» ИИС мы обозначим через V, то полные ресурсы системы будут равны
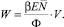(9)
Из уравнения (9) видно, что ресурсы ИИС будут возрастать с увеличением числа каналов связи и канальной емкости системы, т.е. в случае многоканальных ИИС. На сегодняшний день – это один из распространенных видов ИИС, обладающих наиболее высокой надежностью, более высоким быстродействием [5]. Однако они имеют повышенные сложность и стоимость.
Если принять, что ресурсы ИИС экспоненциально возрастают со временем, т.е. имеет место закон Мура [6], то можно записать:
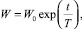(10)
где Т – жизненный цикл ИИС.
Для функции отклика из (10) будем иметь:
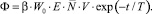(11)
Экспериментально жизненный цикл ИИС можно определять по времени отказа того или иного его структурного элемента, используя большой арсенал имеющихся методов определения надежности электронных систем [7].
В простейшем случае, в качестве функции отклика можно взять отношение выходного сигнала к входному и воспользоваться автокорреляционными функциями процессов на входе и на выходе системы в форме Винера-Ли [8] или в любой другой форме [9].
Заключение
В настоящее время автоматизированное проектирование ИИС представляет собой довольно дорогостоящую процедуру, поэтому весьма полезны простые модели, позволяющие провести качественную, а иногда и количественную, характеристику их основных свойств. Именно это мы и хотели показать в настоящей работе.
Работа выполнена по программе МОН РК 055 «Научная и/или научно-техническая деятельность», подпрограмма 101 «Грантовое финансирование научных исследований». Контракт № 341.