На сегодняшний день одной из важнейших задач технического прогресса в области машиностроения является повышение надежности и долговечности деталей машин. В современных условиях рыночных отношений промышленные предприятия должны предлагать потребителю конкурентоспособную продукцию, обладающую высокой надежностью, производительностью, ремонтопригодностью по ценам ниже мировых. Эта задача может быть решена различными конструктивными и технологическими методами. Одним из эффективных способов повышения эксплуатационной надежности машин является их упрочнение поверхностным пластическим деформированием (ППД). Пластически деформируя неглубокий поверхностный слой металла, как правило являющийся наиболее нагруженным, имеющим микроконцентраторы напряжений от предшествующей обработки, ППД изменяет его физико-механические свойства, реализуя заложенный в металле резерв прочности и пластичности. Поверхностное упрочнение повышает такие эксплуатационные свойства деталей, как их усталостная прочность, коррозионная стойкость, контактная выносливость и износостойкость. Основными упрочняющими факторами ППД являются глубина и интенсивность деформации поверхностного слоя (наклеп) и система остаточных напряжений. На эти показатели качества поверхностного слоя ППД роликами наибольшее влияние оказывает усилие деформирования, максимальные значения нормальных и касательных напряжений, действующие в точке деформации, а также соотношение их значений, определяющих направление деформаций и перемещений металла в зоне контакта. Возможность управления процессом ППД определяется изученностью этого процесса, и при этом желательно иметь количественные оценки происходящих в контактной зоне явлений в виде простых аналитических зависимостей, отражающих влияние всех существующих факторов. Известны методики определения напряженного состояния между контактируемыми телами, в которых исходят из допущений, что контактируемые детали являются абсолютно упругими. Попытка перенести полученные результаты на случай упругопластического деформирования роликами оказалась несостоятельной в виду большого расхождения с экспериментальными данными. В процессе качения ролика на его фронтальной поверхности происходит упругопластическая деформация и интенсивное пластическое течение металла. Впереди ролика образуется волна за счет вытеснения металла из контактной зоны. На противоположной стороне ролика происходит упругое восстановление деформированного слоя. Таким образом, учет реальной формы контакта между роликом и деталью и характера пластического течения металла позволили бы правильно решить задачу нахождения напряженного состояния и учесть динамику процесса деформирования.
При наличии нагружения, не включающего разгрузку, упруго упрочняющееся тело аналогично нелинейно-упругому, в том смысле, что связь между напряжениями и деформациями будет взаимно однозначной. Таким образом, можно считать, что нелинейное упругое тело может быть описано законом Гука, в котором модуль упругости не является постоянным, а зависит от деформаций [2]. Кривую σ-ε в диаграмме растяжение – сжатие можно аппроксимировать степенной зависимостью вида
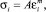 (1)
(1)
где A, m – константы, зависящие от физико-механических характеристик.
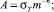
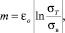 (2)
(2)
где σт – предел текучести; σв – предел прочности.
Таким образом, для вычисления напряжений по формуле (1), необходимо установить деформации поверхности в зоне контакта, или, что тоже самое, кинематику точек деформируемой среды.
В качестве траекторий движения точек обрабатываемой поверхности было принято семейство циклоид, предположив, что нижняя точка С деформирующего ролика в заданном его сечении перпендикулярно оси, в данный момент перемещается без проскальзывания (рисунок).
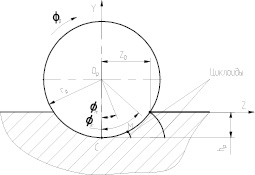
Схема для определения кинематики точек деформируемой поверхности
Движение по циклоидам описывается уравнениями
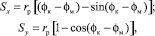 (5)
(5)
где rр – изменение радиуса ролика по длине контакта; φкк – угол контакта, соответствующий полуширине контакта zк; φмм – параметр семейства, соответствующий текущему значению угла контакта 0 ≤ φм ≤ φк.
Произведя преобразования и продифференцировав полученные выражения по z, получим относительные деформации εz и εy.
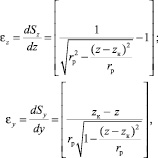 (6)
(6)
где rp – радиус ролика; z – изменение текущей характеристики полуширины контакта.
Анализ формулы (5) и (6) показал, что выбор движения точек деформируемой поверхности по циклоидам является более предпочтительным, т.к. объясняет некоторые экспериментально полученные результаты.
Учитывая связь напряжений с деформациями, определяемой формулой (1), можно определить распределение напряжений по площади контакта на фронтальной поверхности ролика.
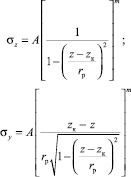 (7)
(7)
Соответственно, нормальные и касательные составляющие усилия деформирования можно определить из зависимостей
 (8)
(8)
 (9)
(9)
где Lк – длина контактной зоны; l – текущее значение длины контактной зоны; zк – изменение полуширины контакта.
Для практических расчетов была рассмотрена обработка цилиндрических поверхностей профильными роликами, дающими при внедрении эллипсный контакт, и была получена формула для определения величины zк, входящей в расчетные зависимости (7), (8), (9):
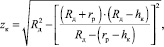 (10)
(10)
где Rд – радиус обрабатываемой детали;
Результаты расчетов, полученные с помощью ПЭВМ по представленным зависимостям (8), (9), показали, что относительная деформация точек деформируемой поверхности, а соответственно и напряжения в зоне контакта в направлениях осей z и y отличается почти на порядок. Это соответствует многочисленным экспериментальным данным о том, что касательная и нормальная составляющие усилия деформирования отличаются друг от друга на тот же порядок, что может служить подтверждением правильности выбранной методики расчета. Таким образом, понимание законов взаимодействия деформирующих роликов с поверхностью детали позволяет получить как закон распределения в контактной зоне, так и составляющие усилия деформирования, необходимые для достижения оптимального качества обрабатываемой поверхности.



