Российская текстильная промышленность переживает на данном этапе своего исторического развития сложную структурную перестройку. Для того, чтобы выжить и остаться на отечественном рынке, ей приходится приспосабливаться к работе в условиях перехода к рыночной экономике. В современных условиях на первый план выдвигается проблема конкурентоспособности продукции предприятия текстильной промышленности на внутреннем и внешнем рынках.
Одним из способов повышения конкурентоспособности производства является как оптимизация системы управления предприятием, так и технологических процессов выработки полуфабрикатов и готовой продукции [1, 2]. В связи с этим задача разработки математических моделей технологических процессов подготовки нитей к ткачеству является актуальной.
Для решения этой задачи на базе приготовительного отдела ткацкого производства ООО «Камышинский текстильный комбинат» был проведён эксперимент по определению оптимальных технологических параметров перематывания пряжи на мотальной машине М-150-2.
Технические параметры пряжи представлены в табл. 1.
Таблица 1
Техническая характеристика пряжи
|
Наименование показателя |
Значение |
|
Вид волокна |
Хлопок |
|
Номинальная линейная плотность пряжи, текс |
18,5 |
|
Удельная разрывная нагрузка, сН/текс |
11 |
|
Коэффициент вариации по разрывной нагрузке, % |
16,2 |
|
Показатель качества (не менее) |
0,69 |
С целью анализа состояния изученности вопроса и с целью обоснования актуальности и научной новизны данного исследования был проведен анализ научных работ [3–7], посвящённых исследованию технологического процесса перематывания основной пряжи, а также проведены исследования технологических параметров заправки 6 мотальных машин, установленных на ООО «Камышинский текстильный комбинат».
В качестве выходного параметра Y выбираем разрывную нагрузку пряжи после перематывания, так как это основной показатель качества пряжи и, исходя из требований к процессу перематывания, он не должен ухудшаться.
Кроме того, этот параметр удовлетворяет следующим требованиям [6]:
1) оценивает эффективность исследуемого объекта;
2) эффективен в статическом смысле, т.е. обладать сравнительно небольшой дисперсией и, следовательно, определяться с достаточной точностью без больших затрат или потерь времени;
3) обеспечивает достаточную полноту описания объекта;
4) имеет простую форму и определенный физический смысл.
На основе ранее произведённых исследований известно, что наиболее важными технологическими параметрами процесса перематывания, влияющими на прочность пряжи являются: Х1 – вес грузовых шайб в натяжном приборе, г; Х2 – линейную скорость перематывания пряжи, м/мин.
В качестве метода исследования данного технологического процесса был выбран активный эксперимент по матрице планирования Коно-2, так как он позволяет получать статические математические модели процессов, используя факторное планирование, регрессионный анализ и движение по градиенту. При этом предполагается, что множество определяющих факторов задано, каждый из факторов управляем, результаты опытов воспроизводятся, опыты равноценны, решается задача поиска оптимальных условий, математическая модель процесса заранее неизвестна. Кроме того матрица планирования Коно-2, близкая к D–оптимальным, обладает свойствами униформности и ротатабельности, имеет малое число опытов. Меньшее число опытов по сравнению с матрицами ротатабельного центрального композиционного эксперимента (РЦКЭ) достигается за счет уменьшения числа опытов, имеющих равные дисперсии выходного параметра [7].
Эксперимент, проведенный по выбранной матрице, позволяет получить математическую модель второго порядка, описывающую влияние факторов Х1, Х2 на выбранный параметр оптимизации Y следующего вида:
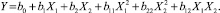 (1)
(1)
Исследование любого технологического процесса начинается с проведения предварительного эксперимента, в результате которого определяются значения основных уровней факторов Хо, интервалы варьирования факторов I, верхние и нижние уровни варьирования – ХВ и ХН. Полученные данные заносятся в табл. 2.
Таблица 2
Условия проведения эксперимента
|
Условие проведения эксперимента |
Кодированные значения i-го фактора |
Натуральные значения i-го фактора |
||
|
х1 |
х2 |
Х1 |
Х2 |
|
|
Основной уровень фактора Хо |
0 |
0 |
11 |
750 |
|
Интервал варьирования фактора I |
1 |
1 |
3 |
50 |
|
Верхний уровень фактора ХВ |
+1 |
+1 |
14 |
800 |
|
Нижний уровень фактора ХН |
–1 |
–1 |
8 |
700 |
По данным активного эксперимента при изучении технологического процесса перематывания получена определенная последовательность выходных данных (табл. 3), отражающих разрывную нагрузку пряжи, после процесса перематывания.
Для обработки данных активного эксперимента и последующей оптимизации технологических процессов была разработана программа в программной оболочке Mathcad «Оптимизация технологических процессов ткацкого производства по данным активного эксперимента, проведенного по матрице планирования Коно-2».
Предлагаемая программа оптимизации технологических процессов, позволяет производить обработку данных активного эксперимента, проводимых по матрице планирования Коно-2, с последующей оптимизацией по методу канонического преобразования математической модели с наглядным представлением поверхности оклика целевой функции.
Программа обеспечивает выполнение следующих функций:
– определение и исключение резковыделяющихся данных;
– определение коэффициентов регрессионного уравнения;
– анализ адекватности полученной математической модели;
– определение оптимальных технологических параметров с построением поверхности отклика целевой функции и её сечения.
В результате обработки данных активного эксперимента получено уравнение регрессии, составленное по формуле (1), описывающее зависимость разрывной нагрузки пряжи от заправочных параметров мотальной машины:
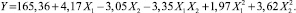
Таблица 3
Результаты эксперимента
|
№ п/п |
Кодированные значения факторов |
Натуральные значения факторов |
Средние значения выходного параметра, полученные в результате эксперимента |
||
|
х1 |
х2 |
Х1 |
Х2 |
|
|
|
1 2 3 4 5 6 7 8 9 |
+ – + – + – 0 0 0 |
+ + – – 0 0 + – 0 |
14 8 14 8 14 8 11 11 11 |
800 800 700 700 750 750 800 700 750 |
166,7 166,7 181,7 168,3 173,3 161,7 168,3 170,0 165,0 |
Получив математическую модель, можно провести ее анализ, то есть по значениям коэффициентов регрессии описать вклад соответствующего фактора в величину выходного параметра. Так для полученного уравнения имеем:
1. Наибольшее влияние на разрывную нагрузку оказывает заправочное натяжение нитей основы, так как коэффициент стоящий перед зависимой переменной имеет наибольшее значение, кроме того, при увеличении массы шайб, значение разрывной нагрузки так же увеличится.
2. Наименьшее влияние на разрывную нагрузку оказывает линейная скорость перематывания, так как коэффициент стоящий перед зависимой переменной имеет наименьшее значение.
Для оптимизации технологического процесса перематывания хлопчатобумажной пряжи линейной плотностью 18,5 текс на мотальной машине М-150-2 с максимальной прочностью был выбран метод канонического преобразования математической модели, который позволяет в разработанной программе получать геометрические представления (поверхности отклика) целевой функции, представленные на рисунок. Кроме того разработанные программы позволяют с помощью встроенной в Mathcad функции оптимизации проводить проверку оптимальных значений полученных при анализе поверхностей отклика целевой функции.
Результаты оптимизации исследуемого технологического процесса перематывания приведены в табл. 4.
Таблица 4
Оптимальные заправочные параметры
|
Кодированные значения факторов |
Натуральные значения факторов |
||
|
х1 |
х2 |
Х1, г |
Х2, м/мин |
|
+1 |
–1 |
14 |
700 |
Таким образом, для перематывания хлопчатобумажной пряжи обладающей максимальной прочностью 181,5 сН необходимо на мотальной машине М-150-2 установить следующие заправочные параметры: массу грузовых шайб в натяжном приборе – 14 г, линейную скорость перематывания – 700 м/мин.
Выводы
1. Для математического описания технологического процесса перематывания и оптимизации его параметров была разработана в программной оболочке Mathcad программа «Оптимизация технологических процессов ткацкого производства по данным активного эксперимента, проведенного по матрице планирования Коно-2».
2. Проведённые экспериментальные исследования зависимости разрывной нагрузки хлопчатобумажной пряжи, перематываемой на мотальной машине М-150-2 от массы шайб в натяжном приборе и линейной скорости перематывания позволили сделать вывод о том, что эта зависимость носит нелинейный характер.
3. Анализ полученного уравнения, позволяет сделать вывод о том, что наибольшее влияние на прочность пряжи, перематываемой на мотальной машине М-150-2, оказывает масса шайб в натяжном приборе, а наименьшее влияние на прочность пряжи, перематываемой на мотальной машине М-150-2, оказывает линейная скорость перематывания.
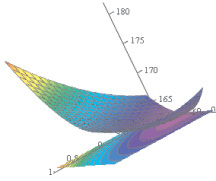
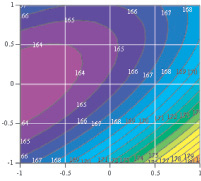
Поверхность отклика и её сечение
4. Получены оптимальные заправочные параметры перематывания хлопчатобумажной пряжи линейной плотностью 18,5 текс на мотальной машине М-150-2 с максимальной прочностью.