Метод конечных элементов (далее МКЭ) в связи с интенсивным развитием вычислительной техники в последнее десятилетие стал активно применяться для численных решений задач из различных областей (механика деформируемого твердого тела, термодинамика, электродинамика и т.д.). Ранее широкому распространению МКЭ мешало отсутствие алгоритмов разбиения области на почти равносторонние треугольники. Методы триангуляции Делоне, а так же другие, позволили создать полностью автоматические САПР, использующие МКЭ.
В основе МКЭ лежит идея замены задачи отыскания самой функции на задачу отыскания конечного числа ее приближенных значений в произвольно выбранных узлах. В одномерном случае для решения подобной задачи выбирается разбиение отрезка на некоторое количество узлов, между которыми задаются отрезки кусочно-полиномиальных функций, которые позволяют провести дальнейшую аппроксимацию к искомой функции. При достаточно большом количестве данных отрезков можно говорить о том, что выполнена сколь угодно точная аппроксимация к искомой функции
Приведем несколько общеизвестных математических выражений из МКЭ [1].
Для одного элемента задается функция q(x), причем – u'' = q(x), u(0) = u(1) = 0, функция u неизвестна. u(x) можно представить в виде линейной комбинации
Далее используется метод Галеркина, позволяющий избежать разрывов непрерывности в узлах.
. φj(х) – функции, совпадающие с пробными функциями, участвующими в записи вышеприведенной линейной комбинации. Дальнейшие преобразования приводят к матричным методам счисления и позволяют представить функции-элементы в удобном для вычислительной техники виде.
Применение МКЭ может существенно упростить задачи проектирования пьезоактюаторов, пьезосканеров и устройств наноперемещений зонда, повысить точность выполнения технологических процессов.
При расчете конструкций, содержащих пьезокерамические элементы в различных программах, использующих МКЭ, необходимо хорошо знать механические свойства используемой пьезокерамики, так как пьезокерамика является анизотропным материалом, а также учитывать состояние пьезоактюатора – он может быть электрически свободен и зажат. Во втором случае пьезокерамика приобретает дополнительную жесткость.
Рассмотрим пример машинного эксперимента. Программа может методом конечно-элементного анализа рассчитать напряжения, деформации и перемещения в конструкции из пьезоэлементов, которые возникают при приложении к подводящим электродам напряжения.
Конструкция имеет конфигурацию пьезотрубки, толщина подводящих электрическое напряжение электродов условно принимается равной нулю (при создании пьезотрубок толщина подводящих электродов подбирается таким образом, чтобы не оказывала влияние на деформации самой пьезотрубки при подаче напряжения). Высота элемента пьезотрубки 2 мм, всего восемь элементов. Внешний диаметр пьезотрубки 10 мм, внутренний – 4 мм. Материал пьезотрубки – пьезокерамика ЦТС-38.
а) 
б)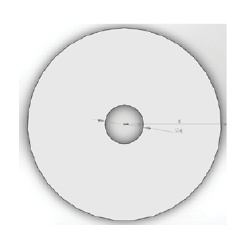
Рис. 1. Вид пьезоактюатора сбоку (а) и сверху (б)
Порядок выполнения машинного эксперимента:
1) Создание элемента-кольца с высотой 2 мм, диаметром 10 мм и внутренним диаметром 4 мм.
2) Создание сборки из восьми жестко скрепленных торцами пьезоколец;
3) Задание материала и справочной геометрии для конструкции;
4) Создание исследования на статические нагрузки, создание сетки элементов и закрепление нижнего торца конструкции;
Рис. 2. Сетка конечных элементов
на исследуемом объекте
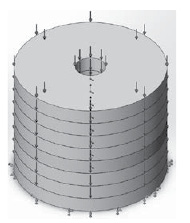
Рис. 3. Схема приложения деформирующей
распределенной силы
5) Приложение деформирующей распределенной силы, равной 100 Н к торцу каждого пьезоэлемента;
6) Дублирование исследования и реверс направления деформирующих сил;
а)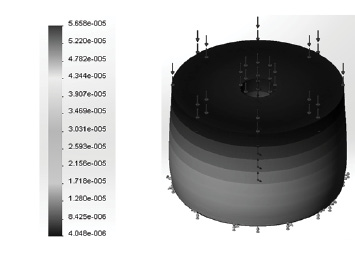
б)
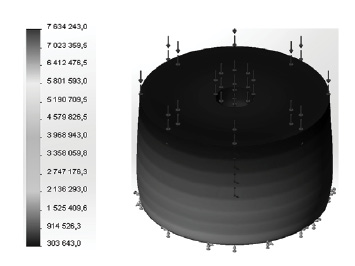в)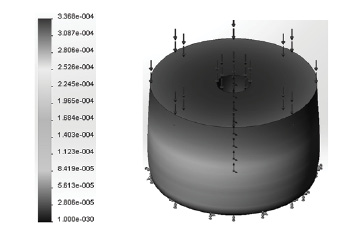
Рис. 4. Результаты работы программы
для случая сжатия пьезоактюатора: деформации (а), напряжения по Мизесу (Па) (б), перемещения (мм) (в)
Как видно из результатов машинного эксперимента, наибольшие деформации и напряжения (5,658×10-5 относительных единиц и 7,634 МПа) возникают в основании (области закрепления образца). Это подтверждается эпюрами аналитических решений задач по прикладной механике.
Наибольший интерес в вопросах исполнения нанотехнологических процессов составляют непосредственно перемещения свободного основания, которые составляют максимально 337 нм. Это перемещение составляет меньше максимально допустимого для пьезоактюатора перемещения в 0,2% длины всего актюатора.
Для того, чтобы проверить точность машинного эксперимента, можно использовать формулу для нахождения абсолютного удлинения одного элемента пьезоактюатора [4].
где ε – диэлектрическая проницаемость пьезокерамики, ε0 – электрическая постоянная, E3 – напряженность электрического поля вдоль направления деформации, l – длина элемента, d33 – пьезомодуль материала вдоль направления деформации, Yz – модуль Юнга вдоль направления деформации.
Напряженность электрического поля можно вычислить по формуле
где Р3 – растягивающая/сжимающая сила (в случае эксперимента 100 Н), F – площадь торцевой грани элемента
F = 66×10-6 м2. Yz = 6.8×1010 Н/м2.
Можно преобразовать формулу абсолютного удлинения.
разница между машинным экспериментом и теорией составляет 356-337 = 19 нм, это абсолютная погрешность. (19/356)×100% = 5,4%. Это свидетельствует об адекватности теоретической модели и машинного эксперимента.
В заключение следует отметить, что метод конечных элементов сложнее известного метода конечных разностей. Однако у МКЭ есть ряд преимуществ, проявляющихся на реальных задачах: произвольная форма обрабатываемой области, сетку можно сделать более редкой в тех местах, где особая точность не нужна.