Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Для обеспечения здоровья нации необходимо вовлечение ее в активную жизнедеятельность, включающую общеоздоровительную физкультуру, туризм, спортивные игры, реабилитационную лечебную гимнастику для больных и раненых. Наряду с известными формами, обращает на себя внимание уже апробированная и эффективная спортивная игра – питербаскет, перспективная в общеоздоровительном плане и для реабилитации инвалидов [8, 9, 27, 36, 37, 40].

Санкт-Петербург – родина отечественного баскетбола. Еще в 1906 году по инициативе С.В. Васильева были проведены первые баскетбольные соревнования. Игра стала национальным достоянием россиян, также как петербургский «Спартак» выдающегося Владимира Кондрашина и великого Александра Белова. Баскетбол входит в число самых любимых игр современности. Эта игра разделила население земного шара на три категории: игравших, играющих и которые будут играть. Триумф создателя баскетбола американца Нейсмита, очевиден, игра получила прописку во всех странах мира. Зрительная аудитория составляет ежегодно более 270 миллионов (из них в своем большинстве болельщики – американцы).

Презентация питербаскета [27] состоялась в декабре 2002 года в Санкт-Петербурге во дворце спорта «Юбилейный» на 9-м международном турнире «Кубок В.Кондрашина и А. Белова». Фактически был представлен упрощенный вариант всемирно известного баскетбола, который позволяет устранить трудности его еще большей популяризации из-за размеров игровой площадки (364 м2), высокого расположения колец (305 см), большого расстояния между ними (26 м) и значительного числа соревнующихся (10 человек). Это особенно остро ощущается теми, кто не обладает всем комплексом двигательных качеств, необходимых для игры в обычный баскетбол. Питербаскет был включен во Всероссийскую универсиаду по летним видам спорта среди студентов, обучающихся по специальности «Адаптивная физическая культура» (физическая культура для лиц с отклонениями в состоянии здоровья, включая инвалидов). Финал состоялся в Санкт-Петербурге с 25 по 30 ноября 2003 г. Это новая спортивная командная игра с мячом с ее разновидностями – питербаскетвалид, ватерпитербаскет, – главным назначением которых явилось упрощение содержания традиционного баскетбола, обеспечивающее доступность игры для всех возрастных групп с различным состоянием здоровья. Другое достоинство состоит в том, что количество игроков может быть неограниченным. Динамичность и эффективность этой игры определены ее центростремительной направленностью. Простота правил, комфортность и эмоциональный настрой питербаскета превращают его в семейную, народную игру, сохраняя при этом признаки спортивной дисциплины, претендующей на олимпийскую. Ее адаптивный вариант – питербаскетвалид – способствует вовлечению в спортивное движение людей с ограниченными физическими возможностями [6, 28–33, 35, 38, 39].

С помощью физических упражнений люди с заболеваниями опорно-двигательного аппарата значительно расширяют свою двигательную сферу; с отклонениями в развитии интеллекта – осваивают сложные двигательные программы различных видов спорта. Доступные занятия физической культурой и спортом для людей с отклонениями в здоровье становятся важным условием их полноценной жизни, создают начальную базу для развития двигательных способностей, раскрыть которые дает возможность адаптивный спорт [3, 34].

Для развития адаптивного спорта новых дисциплин необходима современная научно-методическая база, которой может стать основанная на теории хаоса и самоорганизации (ТХС) – третья синергетическая парадигма [19, 22].

В восьмидесятых годах прошлого века возникла наука, получившая название синергетика, что в переводе с греческого означает совместное кооперативное действие. Эта наука является интегрирующей, объединяя общими законами разные области наук: физику, химию, биологию, психологию, социальные науки, астрономию, философию и т.д. В частности, синергетика впервые сформулировала универсальные законы эволюции, справедливые как для физического (косного), так и для биологического (живого) мира и социума. На смену ей приходит ТХС [14].

Синергетическая педагогика спорта – система взаимодействия тренера и спортсмена, обладающая эффектом нового качественного повышения творческого потенциала коллектива, обеспечивающая реализацию новой цели – обучения коллектива с получением побочного творческого продукта силами учащихся. При этом новые средства компьютерной среды оптимизирует коммуникацию и разработку информационного продукта. Такая педагогика спорта пользуется новыми методами обработки информации для реализации обучения [10], а также аккумулирует знания, отражающие особенности деятельности функциональных систем человеческого организма. Имеется глубинное родство между деятельностью тренера и спортсмена. И то, и другое – являются формами творчества. Искусство тренера имеет дело с материальным «предметом» – биологическим объектом, который надо трансформировать в соответствии с поставленной целью (достижения определенного результата). Но обязательно – во взаимодействии с обучающимися, функциональные системы которых имеют хаотическую вариантность и могут обеспечивать непредсказуемый результат.

Имеется достаточно доказательств того, что синергетика является третьей глобальной парадигмой (исторически: первая – детерминистская, вторая – стохастическая). Недооценка этого факта учеными, всем интеллектуальным сообществом – тормозит динамичное развитие спорта и человечества в целом [23]. В науке существует полная определенность (в рамках детерминистской парадигмы), частичная неопределенность (в рамках стохастической парадигмы) и полная неопределенность (в рамках синергетической парадигмы).

Установлено, что структурная организация природных систем, в том числе и анатомическое строение человеческого тела, характеризуется наличием золотого сечения (ЗС) – объективной гармонией. При этом зрительная система человека способна выделять объекты, имеющие соразмерность ЗС, как красивые и совершенные – субъективная гармония. То же самое было установлено и в отношении слухового анализатора. При этом важно расположение чувствительных концов анализаторов в коре головного мозга у человека. Соматосенсорная (чувствующая тело) область S1 расположена в задней центральной (постцентральной) извилине позади глубокой центральной (роландовой) борозды головного мозга. В ней соматическая (телесная) чувствительность представлена головой вниз и вверх ногами – «сенсорный гомункулус», в котором кисть занимает обширную зону, причем, с хорошей пространственной разрешающей способностью [42]. Изображения над поперечным срезом мозга (на уровне постцентральной извилины) и их обозначения демонстрируют пространственное представительство поверхности тела в коре, установленное путем локальной электрической стимуляции мозга бодрствующих больных. Область SH расположена у латерального конца задней центральной извилины (нижняя стенка сильвиевой борозды) головного мозга. Она считается местом билатерального (двустороннего) восприятия, например, при ощупывании предметов обеими руками (бимануальном исследовании). В связи с тем, что тело по своей анатомической конструкции (в том числе и кисть) построено по закону ЗС и золотого вурфа, то их проекция в соматосенсорной коре соответствует тому же закону при нормальном телосложении человека. Но сенсорный гомункулус включает не только анатомическую проекцию, но воспринимает и функциональный статус человеческого тела, например, локомоцию. Поэтому гармонические параметры ходьбы в произвольном темпе отражены в том же гомункулусе [43].

Двигательная область коры находится в передней (прецентральной) извилине (поле 4 по Бродману) головного мозга. Двигательные (моторные) функции в ней представлены тоже вниз головой и вверх ногами – «двигательный гомункулус». При этом кисть в ней занимает тоже большую зону, что связано с ее ролью в трудовых процессах, особенно требующих тонких и точных движений. Кроме первичной, имеется и вторичная моторная область, которая находится спереди от прецентральной извилины и выполняет более сложные функции, например, движения всей конечности. В ней различают медиальную и латеральную зоны и называют премоторной корой (поле 6 по Бродману). Считается, что высшие двигательные функции зарождаются в этом поле. Кроме двигательной и сенсорной коры, имеется так называемая ассоциативная (неспецифическая) кора. Она выполняет высшие психические функции кортико-кортикальных связей (ассоциаций). Различают 3 вида ассоциативной коры: 1) теменно-височно-затылочную (ТВЗ); 2) префронтальную; 3) лимбическую. Особый интерес представляет ТВЗ-ассоциативная кора. Бернштейном Н.А. описаны уровни построения движений, самый низший из которых – уровень палеокинетических регуляций. У человека – это руброспинальный уровень А. Самым важным считается таламопалидарный уровень В. Это уровень синергии и паттернов и касается он «локомоторной машины, оснащенной конечностями – движителями». Следующий высший уровень построения движений – пирамид-ностриальный или пространственный уровень С. Наконец, уровень предметных действий Д – специфически человеческий уровень для смыслового решения задач (бритье, очинка карандаша и др.) с участием руки. Сюда же отнесена речь, как высшая форма действий. Отмечается, что премоторная зона обеспечивает двигательные навыки, сноровку, ловкость рук и т.д. [4].

Формирование золотого алгоритма управления двигательными функциями зависит от характера задачи. Если речь идет о циклической деятельности (ходьба), то происходит простое включение подкоркового «автомата» – таламопалидарной системы головного мозга, работающей в режиме ЗС. Если же стоит задача по оптимизации тренировочного процесса, то алгоритм управления формируется в ТВЗ-ассоциативной коре и уточняется на принципе обратной связи (стереогностической и зрительной) в премоторной и моторной коре мозга с учетом ЗС. При изучении механизма реакций организма на гармонические сигналы, необходимо учитывать возможный «психический резонанс» на воздействие раздражителей в режиме ЗС. У человека в качестве таких резонаторов рассматриваются нижние конечности, инспираторный и экспираторный аппараты внешнего дыхания и др., а связующей средой – соответствующие нервные центры. Роль резонаторов и активной среды – плазмы крови выявляется при изучении физиологии крови и структуризации тезиограмм биологических жидкостей. Активная среда при этом – плазма крови, а резонаторы – клеточные или молекулярные компоненты крови. Дегидратация этих биологических жидкостей ведет к образованию паттернов золотой пропорции [24].

С позиции синергетического анализа физиологические основы визуального восприятия при тренировках спортсменов подтверждают один из основных принципов существования сложных человекомерных систем. Это – самоорганизация – selforganization [23]. Это явление присуще спортсменам, обеспечивающим высшие достижения, рекорды. Человеческий организм обладает самоорганизующимися физиологическими системами разных уровней, в том числе на уровне головного мозга, обеспечивающими зрительное восприятие гармонических движений в тренировочном и соревновательном периодах, и представляющие плацдарм для реализации педагогических идей, получающих мощный инструмент достижения своих целей. Сопряженность функций человеческого организма с функциональной деятельностью мозга, обуславливающая особенности локомоторного (мышечно-двигательного) аппарата человека, характер эстетического восприятия зрительным аппаратом окружающего мира – должны учитываться при обучении различным видам спорта, когда малозначимые для окружающих детали способны, как джокер[1], резко изменить характер подготовки спортсмена. Двигательные навыки, локомоторное обеспечение владения спортивными снарядами (ядро, копье и др.) и мячом (в баскетболе, волейболе, футболе) – также зависят от взаимодействия центральной нервной системы, специализированных отделов мозга и состояния мышечного аппарата. Но такая конвергенция будет не полной, если не развиты когнитивные функции, сознание, а также отсутствует духовный стимул.

Непредсказуемость великих спортсменов (признанных и непризнанных) – это и есть проявление регулируемого, организованного хаоса. Так, в боксе свободная, раскрепощенная манера Роя Джонса младшего, исходящая из особенностей физиологии спортсмена, обеспечила в определенный период его доминирование сразу в нескольких весовых категориях (средней, второй средней, полутяжелой и тяжелой). То же – у Шугара Рэя Леонардо (от полусредней до полутяжелой весовой категории). Каждый великий спортсмен индивидуален, а его техника порой резко отличается от общепризнанной и детерминистски обусловленной. Именно эта индивидуальность является примером организованного хаоса, инициируемого физиологическими особенностями (а не константами) организма спортсмена.

В.М. Еськовым предложен новый метод идентификации матриц межаттракторных расстояний, который позволяет оценить степень влияния физической нагрузки на организм человека [20, 25]. Данный метод используется для групповых сравнений (разных групп людей, разных видов воздействий, разных видов лечебно-оздоровительных мероприятий, физических нагрузок или видов спорта), когда имеются несколько кластеров данных (для каждой группы обследуемых, или для каждого типа воздействий для группы обследуемых) и эти кластеры описываются своим вектором состояния организма человека (ВСОЧ). Интегративной мерой оценки эффективности лечебного или физкультурно-спортивного воздействия является степень близости (или, наоборот, удаленности) этих 2 сравниваемых квазиаттракторов в фазовом пространстве состояний (ФПС). При этом каждый человек со своим набором признаков (компонентов ВСОЧ) задается точкой в этом ФПС так, что группа испытуемых образует некоторое «облако» (квазиаттрактор) в ФПС, а разные группы (из-за разных воздействий на них) образуют разные «облака» – квазиаттракторы в ФПС. Расстояния Zij – (здесь i и j – номера групп обследуемых) между хаотическими центрами этих разных квазиаттракторов формируют матрицы Z, которые задают все возможные расстояния между их хаотическими центрами, описывающие состояние разных групп обследуемых до начала физкультурного воздействия и после физкультурного воздействия. Причем, максимальные различия в расстояниях между хаотическими центрами квазиаттракторов Zij движения ВСОЧ разных групп испытуемых (до и после определенного воздействия) соответствуют максимальной эффективности физкультурно-спортивного мероприятия, а их уменьшение требует дополнительной корректировки в физкультурном воздействии [12, 20, 26].

Так, в одном из множества исследований участвовали студенты Сургутского и Самарского университетов (юноши и девушки) с разным уровнем физической подготовки. Показатели снимались до и после физической нагрузки. Обследуемых юношей условно разделили на три группы: 1 группа – студенты, занимающиеся игровыми видами спорта (футбол, волейбол, баскетбол); 2 группа – студенты, занимающиеся индивидуальными видами спорта (тяжелая атлетика, пауэрлифтинг); 3 группа сравнения – студенты, занимающиеся физической культурой (ФК) не регулярно, а лишь 2 раза в неделю в рамках государственной программы по ФК. Обследуемых девушек условно разделили на две группы: 4 группа – студентки, занимающиеся игровыми видами спорта (футбол, волейбол, баскетбол); 5 группа сравнения – студентки, занимающиеся физической культурой (ФК) не регулярно (2 раза в неделю в рамках государственной программы по ФК). Аналогичное разделение было выполнено и для самарских студентов. Показатели вегетативной нервной системы (ВНС) – табл. 1-4 являются координатами ВСОЧ (x0=СИМ – симпатической, x1=ПАР – парасимпатической, x2=ИНБ – индекса Баевского, x3= SPO2, x4=ЧСС).

Изучены результаты идентификации матриц межаттракторных расстояний Zij между хаотическими центрами квазиаттракторов ВСОЧ тренированных и нетренированных девушек и юношей г. Сургута до и после предъявления нагрузки в 5-мерном фазовом пространстве в сравнении с представителями Самары. Анализ их показал, что наименьшее межаттракторное расстояние Z32=3,23 у.е. получается при сравнении 3 и 5 групп юношей и девушек соответственно, а наибольшее – при сравнении спортсменок девушек 4 группы и юношей 2 группы и составляет Z21=41,10 у.е. В данном сравнении дифференцировка по полу менее значима, чем предъявляемая нагрузка, что отражают результаты табл. 1.

Продолжая анализ матриц межаттракторных расстояний при дифференцировке по полу после предъявления нагрузки, отметим наибольшее межаттракторное расстояние Z12=444,05 у.е. при сравнении девушек 5 группы с юношами 1 группы наблюдения и наименьшее расстояние Z31=22,07 у.е. при сравнении 4 группы девушек с юношами 3 группы.

Таблица 1

Матрицы идентификации расстояний Zij между хаотическими центрами квазиаттракторов вектора состояния организма тренированных (1 и 2 группы юношей и 4 группа девушек) и нетренированных (3 группа юношей и 5 группа девушек) студентов г. Сургута до предъявления нагрузки в 5-мерном фазовом пространстве

В качестве xi выступали: x0 – СИМ, x1 – ПАР, x2 – ИНБ – все в у.е., x3 – SPO2 – содержание оксигемоглобина в крови испытуемых (%), x4 – ЧСС – частота сердечных сокращений (уд./мин).

Установлено, что большие межаттракторные расстояния отмечаются при сравнении всех групп юношей с 4 группой девушек. После полученной нагрузки ситуация меняется: большие межаттракторные расстояния отмечаются при сравнении всех групп юношей с 5 группой девушек. Это свидетельствует о стабилизирующем влиянии физической нагрузки на параметры ФСО тренированных студентов, а также об определенной однотипности реакции функциональных систем тренированных на нагрузки (табл. 2).

Таблица 2

Матрицы идентификации расстояний Zij между хаотическими центрами квазиаттракторов вектора состояния организма тренированных (1 и 2 группы юношей и 4 группа девушек) и нетренированных (3 группа юношей и 5 группа девушек) студентов г. Сургута после предъявления нагрузки в 5-мерном фазовом пространстве

Анализируя матрицы идентификации расстояний Zij между хаотическими центрами квазиаттракторов ВСОЧ – тренированных и нетренированных девушек и юношей г. Самары до предъявления нагрузки в 5-мерном фазовом пространстве – наименьшее Z32=2,56 у.е. и получается при сравнении 3 и 5 групп юношей и девушек соответственно (что также отмечено при аналогичном сравнении в г. Сургуте) и при сравнении 1 и 4 групп Z11=2,33, а наибольшее – при сравнении спортсменок девушек 5 группы и юношей 2 группы и составляет Z22=39,03 у.е. (табл. 3). Табл. 4 описывает матрицы межаттракторных расстояний при дифференцировке по полу после предъявления нагрузки.

Таблица 3

Матрицы идентификации расстояний Zij между хаотическими центрами квазиаттракторов вектора состояния организма тренированных (1 и 2 группы юношей и 4 группа девушек) и нетренированных (3 группа юношей и 5 группа девушек) студентов г. Самары до предъявления нагрузки в 5-мерном фазовом пространстве

Таблица 4

Матрицы идентификации расстояний Zij между хаотическими центрами квазиаттракторов вектора состояния организма тренированных (1 и 2 группы юношей и 4 группа девушек) и нетренированных (3 группа юношей и 5 группа девушек) студентов г. Самары после предъявления нагрузки в 5-мерном фазовом пространстве

Установлено, что наибольшее межаттракторное расстояние Z12=444,05 у.е. наблюдается при сравнении девушек 5 группы с юношами 1 группы наблюдения (аналогичная ситуация отмечена в г. Сургуте) и наименьшее расстояние Z32=29,21 у.е. при сравнении 5-й группы девушек с юношами 3 группы.

Анализ показал схожие результаты при сравнении юношей и девушек двух городов. Однако в г. Самаре расстояния в 2 раза меньше, чем в г. Сургуте, что говорит о существенном влиянии условий проживания на параметры их функциональных систем.

В естествознании при описании сложных биосистем (complexity) наступил кризис. Человечество реально подошло к осознанию, пониманию необходимости изучать хаотические процессы и объекты в природе, но делать это в рамках детерминистско-стохастического подхода (ДСП) уже невозможно. В рамках этих новых утверждений и подходов (на основе ТХС) сейчас можно говорить об основных параметрах порядка (ПП) наступившего кризиса.

Реальные биологические динамические системы (БДС) удовлетворяют пяти основным (синергетическим) свойствам, а их описание должно согласовываться с 13 основными отличиями хаотических объектов от объектов со свойствами ДСП (и процессов), т.е. это все в корне расходится с представлениями ДСП и противопоставляется всем подходам формального описания природных объектов (табл. 5).

Таблица 5

Различия в подходах между детерминистско-стохастической парадигмами (ДСП) и синергетической парадигмой (СП), основанной на ТХС

Реальные БДС являются «мерцающими» объектами, которые при этом еще и непрерывно эволюционируют. Это означает (в рамках ТХС), что вектор состояния любой биосистемы (со свойствами complexity и синергетическими, самоорганизующими свойствами) совершает постоянное движение в ФПС в пределах некоторых объемов (называемых квазиаттракторами), а сами эти объекты VG (квазиаттракторы) тоже дрейфуют (эволюция БДС). Простейший способ формализации – определять параметры квазиаттракторов, считать распределение ВСОЧ равномерным и научно обосновывать внешние управляющие воздействия (ВУВ) для прогноза поведения БДС в ФПС. Однако при этом придется отказаться от правила трех сигм (в стохастике значения выходящие за три сигмы – отбрасываются), ввести аналог закона больших чисел в ТХС и учитывать 5 свойств реальных БДС, а также жестко учитывать все 13 существенных отличий ТХС от ДСП [12, 13, 16, 21].

На сегодняшний день существует достаточное количество методов идентификации хаотических режимов БДС, но все они страдают неопределенностью, кроме одного – идентификации свойства перемешивания. Но все известные методы базируются или на длительном наблюдении БДС (поведения ее ВСС в ФПС), что не имеет смысла из-за свойств «мерцания» и эволюции любой биосистемы, или на изучении поведения формальных моделей БДС. В последнем случае сразу возникает задача адекватности данной математической модели конкретной БДС. А это означает, что надо повторять многократно опыты и проверять подобие поведения БДС модельным. Проверка моделей БДС в ТХС – задача практически невыполнима для реальных биосистем (они неповторяемые в принципе!).

Существует большое количество определений и проблем, возникающих при использовании БДС в идентификации хаотических режимов поведения БДС, которые накладывают принципиальные ограничения на использование ДСП в описании и прогнозировании реальных биосистем [41, 45]. Проблема идентификации хаотических режимов поведения БДС наталкивается на целый ряд методических сложностей и становится практически неразрешимой в рамках ДСП. Единственное, что возможно в этой ситуации – это использование свойства перемешивания или просто постулирования хаотического режима поведения ВСОЧ в ФПС. Последнее и производилось авторами многократно применительно к сложным системам [12, 13, 14, 17, 18, 21, 41, 45].

Известны работы, когда в лабораторных условиях исследовались микродвижения при произвольном удержании суставного угла. Эксперименты, проводимые М.А. Айзерманом, Е.А. Андреевой [1], В.И. Черновым [44] показали, что в условиях прицеливания тремор является результатом работы системы, управляющей поддержанием суставного угла. В ходе этих экспериментов четко выделялись его колебания с частотой около 10 Гц, а низкочастотные колебания, хорошо видимые в физиологическом треморе, оказались весьма незначительными. Иными словами, переход от обычного тремора к режиму прицеливания связан с существенным уменьшением низкочастотных колебаний. Во всех этих исследованиях микродвижения конечности фиксировались пьезодатчиками, которые не регистрируют постоянные смещения (с постоянной скоростью движения). Были изменены методика и аппаратура выполняемых биофизических исследований включением в в эту систему новые токовихревые (безинерционных) датчиков измерения тремора, что резко изменило картину вектора в ФПС и существенно дополнило уже имевшиеся ранее [1, 44] данные о произвольности тремора.

В работе использовался автоматизированный комплекс на базе токовихревых датчиков [16], что позволило фиксировать даже медленный дрейф («уход» от цели путём постоянного смещения), что трудно сделать в системах с тензодатчиками. Для регистрации микродвижений токовихревым датчиком использовалась металлическая пластинка, которая крепилась к пальцу испытуемого. Сначала регистрировалась кинематограмма микродвижений пальца руки в состоянии покоя, затем (не прерывая запись) испытуемому давали задание на активное удержание позы – «прицеливание», а через несколько секунд следовала команда «отбой» с продолжением регистрации микродвижения конечности [5].

Треморограммы обрабатывали по специальным программам, которые включали: получение амплитудно-частотной характеристики (АЧХ), построение траектории движения ВСС управления (организации) тремора в координатах 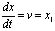и x=x2 (x – координата смещения конечности. dx/dt – скорость смещения) и расчет полученных квазиаттракторов движения ВСС в этом двумерном фазовом пространстве. Одновременно производилось нахождение энтропии Шеннона для процесса тремора и величины дивергенции Кулбака-Лейблера [7].

Разработка хаотических методов регуляции в изучении структуры поведения любых физиологических функций организма человека стало основой для разработки за последние 20 лет новых программных продуктов, устройств и теорий в области ТХС [11, 16]. Обработка данных производилась по специальной запатентованной программе и методу, которые обеспечивали по полученным частотным характеристикам, кинематограммам и полученным из них значениям скоростей (после дифференцирования сигнала) построение фазовых плоскостей (координаты x и V = dx/dt), а также определение границы движения вектора состояния руки (во время тремора) в этом ФПС и оценку размерности квазиаттрактора ФПС, в пределах которого движется вектор [13].

Одновременно выполнялось компартментно-кластерное моделирование этих процессов [5, 13]. Исходно возможны два подхода в моделях: модели на однокластерном (эффекторном) уровне, например, в виде трехкомпартментных систем и модели иерархические. Существенно, что такая иерархическая система не носит характера прямого (direct control) управления [5]. В исследованиях представлены результаты моделирования в рамках однокластерных, трехкомпартментных моделей, которые являются синонимами моделей В.А. Антонца для описания работы нейромоторных композиций, состоящих из трех блоков (компартментов) [2]. Одна из главных проблем организации и управления параметрами тремора связана с уровнем (степенью) хаотичности поведения исследуемых процессов. Иными словами произвольные или непроизвольные движения лежат в основе постурального тремора. Однако, эта проблема связана с более обширными теоретическими предположениями и касается глобальной проблемы роли хаоса в обеспечении жизнедеятельности особых животных организмов и человека в частности.

Известно, что достижения спортсменов во многом зависят от их первичного отбора, когда кроме общефизических данных необходимы специальные навыки или специальные физиологические параметры. Именно для решения задач первичного отбора и направлены усилия авторов настоящего сообщения. Однако разработанные методы могут быть использованы и для оценки качества тренированности и оценки самих тренировок у высококвалифицированных спортсменов, занимающихся пулевой стрельбой, биатлоном и стрельбой из лука, метанием, работой с мячом (баскетбол, волейбол, футбол). Возможно построение фазовой плоскости и обработка данных в терминах квазиаттракторов, т.е. областей, внутри которых хаотически движутся векторы состояний исследуемых процессов (физиологический тремор) [15]. По полученным кинематограммам были построены фазовые портреты микродвижений в координатах Х (удаление пальца от датчика) и V=dX/dt (скорость перемещения пальца). Аналогичное исследование микродвижений конечности проводилось В.А. Антонцом [2] в условиях статической нагрузки на предплечье, причем для регистрации микродвижений конечности использовался пьезоакселерометр, а фазовый портрет микродвижений строился в координатах амплитуды сигнала и ее производной. Проводился сравнительный анализ поведения динамической системы управления движениями в режиме покоя и прицеливания на фазовой плоскости методом многомерных фазовых пространств [5], в данном случае размерность фазового пространства была равна двум. Полученные значения объёмов квазиаттракторов изображающей точки были: до прицеливания – 2,2 E-05; во время прицеливания – 4,6 E-06, то есть объем уменьшился в 4,8 раза, что характеризует изменение состояния системы в сторону меньшей степени хаотичности. Следует отметить, что предлагаемый метод фазовых пространств (на основе измерений квазиаттракторов, позволяет давать оценку квалификаций испытуемого на предмет их подготовки).

Статистическое моделирование с использованием компартментных моделей непроизвольных колебаний конечности, проведенное В.А. Антонцом и Э.П. Ковалевой [2], было основано на вероятностном распределении рекрутирования двигательных единиц (ДЕ), развивающих мышечное напряжение для удержания положения конечности человека. Модель общего состояния мышцы описывается вектором вероятности pt, компоненты которого – вероятности сокращения каждой ДЕ в данный момент времени 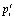, в предыдущий момент 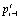и последующий :

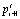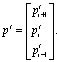
Таким образом, В.А. Антонцом впервые была предложена система трех уравнений, которая позволяет найти зависимость флуктуации силы, развиваемой мышцей, от нагрузки на нее в виде трехкомпартментной системы. В рамках такой теории отрицается существование квазипериодических автоколебаний, т.к. процесс рассматривается как чисто стохастический. В действительности, в рамках классических физиологических представлений, регуляция позы с помощью мышц (в том числе и положение данной конечности в данной точке пространства) должна рассматриваться на более высоком уровне регуляции с позиций общей теории управления. При таком подходе возможно использование компартментного анализа, однако теперь компартментами являются не отдельные совокупности ДЕ, реализующие управляющее воздействие со стороны ЦНС, а компартменты (блоки) аффекторных и эффекторных анализируемых управляющих органов.

Выбор компартментного подхода диктовался возможностью учета наибольшего числа базовых биологических принципов: пуловая (постулируемая Г. Хакеном в синергетике) организация управления биосистемами, диссипативность структур, наличие тормозных и возбуждающих процессов, существованием информационных и возбуждающих связей между пулами (компартментами), выполнение принципов оптимального управления, иерархичность в организации движений. Интегральная выходная биоэлектрическая активность НМС (y), которая определяет частотную характеристику тремора (является объектом управления) в этом случае зависит от состояния компартментов линейно, т.е.

y = c1x1+ c2x2+ c3x3= cTx, (1)

(xi – состояние активности i-го компартмента мотонейронного пула, ci – весовой коэффициент вклада xi в y). Скорость изменения активности (возбуждения) каждого компартмента системы (мышцы) в общем виде находится по формуле

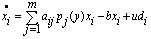, (2)

при i = 1,..,m; i ≠ j. В данной формуле aij – весовой коэффициент влияния j-го компартмента на i-тый (условие i ≠ j показывает, что мотонейронный пул не может влиять сам на себя), pj(y) – описывает тормозную связь, обеспечивающую перекрытие возбуждающих потоков между компартментами (отрицательная обратная связь), b – коэффициент диссипации (рассеяния) возбуждения, u – скалярная величина внешнего воздействия (например, управляющих драйвов), di – весовой коэффициент влияния управляющего драйва на i-й компартмент [5, 13].

Очевидно, наиболее простая система управления движениями с m = 3 и числом кластеров n = 2 (двухкластерные системы). Причем верхний кластер (n = 1) осуществляет управляющие тонические воздействия, и одновременно первый кластер может регулировать амплитуду и частоту колебаний нижнего (мышечного) кластера, за счет этих управляющих воздействий. При этом уменьшается, фактически, стохастичность (хаотичность!) биосистемы. Однако, сама амплитуда колебаний при этом увеличивается за счет притока дополнительного управляющего возбуждения со стороны кластера верхнего уровня иерархии на нижний мышечный кластер.

Таким образом, в предложенном обзоре представлены исследования, позволяющие использовать основные положения ТХС, уже разработанные программные продукты – при внедрении в обиход новой спортивной специализации, вида спорта –и по-новому организовать учебно-тренировочный процесс в будущем олимпийском виде спорта. Это является российским приоритетом.