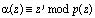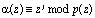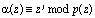Использование цифровых методов представления, обработки и передачи приводит к многократному увеличению занимаемой полосы частот и, как следствие этого, к многократному увеличению скорости передачи информационных сообщений. Решение данной проблемы лежит в области разработки эффективных методов реализации цифровой обработки сигналов (ЦОС). Отмеченные обстоятельства обусловили повышенный интерес разработчиков систем связи к использованию методов цифровой обработки сигналов в различных областях, начиная с обработки речи, заканчивая обработкой изображения. Повысить эффективность реализации ЦОС возможно за счет применения математической модели, поддерживающую параллельную обработку исходных данных.
Основная часть. Основным содержание цифровой обработки сигнала является извлечение полезной информации относительно объекта, который является источником информации, либо относительно среды, через которую сигнал проходит. Сложность алгоритмов, используемых для обработки сигнала, определяются такими факторами, как структура сигналов, их количество, частотный диапазон, необходимая разрешающая способность, тип источников обрабатываемых сигналов, условия распространения сигнала от источников на вход системы обработки. При этом эффективность работы системы ЦОС, ее производительность, надежность, габаритные размеры и потребляемая мощность тесно связаны с требуемой точностью вычислений, которая определяется форматами используемых данных, диапазоном частот входных сигналов, объемами обрабатываемой информации и особенно алгоритмом реализации.
Существующая в последние годы тенденция в цифровой вычислительной технике тенденция к распараллеливанию вычислений связана с непрерывным ростом требований к производительности вычислительных устройств ЦОС. Среди методов обработки данных в реальном масштабе времени наиболее оптимальными для микроэлектронной реализации считаются методы, базирующиеся на нейросетевом базисе.
Однако предъявляемые жесткие временные ограничения и отсутствие высокопроизводительной нейросетевой базы ЦОС является основным сдерживающим фактором широкого внедрения методов цифрового преобразования сигналов в системах передачи речи со сжатием, статистическим уплотнением, пакетной коммутацией, IP-телефонии и других инфотелекоммуникационных системах.
Требования высокой точности и высокой скорости обработки сигнала, предъявляемые к современным системам цифровой обработки сигналов, обуславливает активизацию работ по применению математических моделей ЦОС, обладающих свойством кольца или поля. Ввиду изложенного положения дел на текущем этапе внедрения методов цифровой обработки сигналов в системы обработки и передачи информации вполне понятна актуальность исследований по разработке высокоскоростных параллельных спецпроцессоров ЦОС, поддерживающих целочисленную арифметику, реализованных на основе нейросетевого базиса.
Проведенные исследования методов ЦОС показали, что реализация ортогональных преобразований сигналов в реальном масштабе времени возможно лишь на основе специализации вычислительных средств. Под данной процедурой понимается распараллеливание вычислений на одновременно работающем множестве процессоров, что позволяет в рамках существующих ограничений на массогабаритные характеристики добиться больших функциональных возможностей. Наиболее перспективным направлением распараллеливания вычислений является использование непозиционных систем, в частности, полиномиальной системы классов вычетов (ПСКВ). Если в качестве оснований алгебраической системы выбрать минимальные многочлены 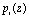 поля
поля 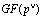 , то полином
, то полином 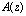 , удовлетворяющий условию
, удовлетворяющий условию 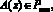 где
где 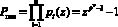 – полный диапазон, представляется в виде
– полный диапазон, представляется в виде
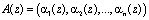 , (1)
, (1)
где 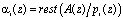 ,
, 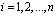 .
.
Рассмотрим выполнение модульных арифметических операций в ПСКВ. Пусть степень минимального многочлена 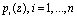 , равна mi. Тогда первый операнд имеет вид
, равна mi. Тогда первый операнд имеет вид
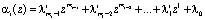 .
.
Соответственно для второго операнда получаем
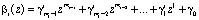 .
.
Тогда для многочленов
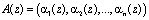
и 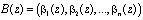 , справедливо:
, справедливо:
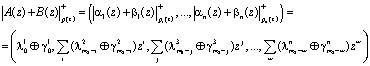 , (2)
, (2)
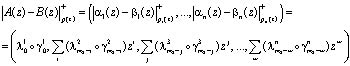 , (3)
, (3)
В силу дистрибутивности операции умножения операндов над кольцом на элементы этого кольца относительно операции сложения справедливо
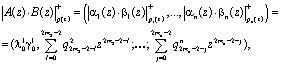 (4)
(4)
где 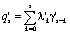 – линейная свертка;
– линейная свертка; 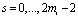 ,
, 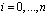 .
.
Рассмотрим пример. Пусть задана ПСКВ с модулями p1=z+1; p2=z3+z2+1; p3=z3+z+1 и диапазоном
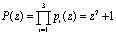 ,
,
а также два полинома
A(z)=z4+z3+z=(1, 0, z2+z+1)
и B(z)= z2+z+1=(1, z2+z+1, z2+z+1).
Тогда справедливо
|
Сумма двух полиномов |
Произведение двух полиномов |
|
C(z)=A(z)+B(z)=z4+z3+z2+1=(0, z2+z+1, 0) |
C(z)=A(z)B(z)=z6+z2+z=(1, 0, z+1) |
|
A(z)= (1, 0 , z2+z+1) B(z)= (1, z2+z+1, z2+z+1) C(z)= (0, z2+z+1, 0 ) |
A(z)= (1, 0 , z2+z+1) B(z)= (1, z2+z+1, z2+z+1) C(z)= (1, 0 , z+1 ) |
Наряду с модульными операциями непозиционный СП, функционирующий в ПСКВ, выполняет и немодульные процедуры. К ним можно отнести прямое и обратное преобразование кодов [3], вычисление позиционных характеристик [3] , определение интервала [3], расширение системы оснований [3], вычисление коэффициентов обобщенной полиадической системы [3], определение «спектральных составляющих» кода ПСКВ [3].
Первой обязательной немодульной операцией является прямое преобразование из позиционного кода в код ПСКВ [4]. Образование остатка αi(z) полинома A(z) осуществляется
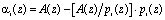 (5)
(5)
где 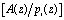 – наименьшее целое от деления A(z) на pi(z); i=1,2,…n.
– наименьшее целое от деления A(z) на pi(z); i=1,2,…n.
В полиномиальной системе классов вычетов выражение (5) можно представить в виде
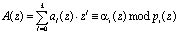 . (6)
. (6)
В настоящее время наибольшее распространение получили следующие методы реализации. В основу первого положен метод понижения разрядности, который определяется
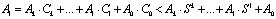 , (7)
, (7)
где Ci – остатки от деления на pi степеней основания, которые дадут набор
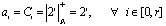 . (8)
. (8)
Основным достоинством данного метода является то, что выполнения используется позиционный сумматор. Однако метод понижения разрядности носит последовательный характер, в результате чего характеризуется значительными временными затратами [4].
Чтобы исправить данный недостаток был разработан итеративный алгоритм прямого преобразования ПСС-ПСКВ, который определяется выражением
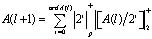 , (9)
, (9)
где l=0,1,2… – число итераций.
Данный алгоритм может быть реализован в виде параллельного конвейера, что позволяет повысить скорость перевода входных данных. Однако, в результате этого, значительно возрастают аппаратурные затраты [5].
В основу работы преобразователей ПСС-ПСКВ может быть положен метод непосредственного суммирования, который задается равенством
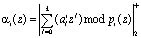 , (10)
, (10)
где 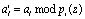 ,
, 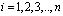 .
.
Как показано в работе [4], этот алгоритм требует минимальных схемных затрат и может быть реализован в виде двухслойной нейронной сети. Рассмотрим пример. Необходимо определить остаток полинома 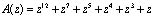 по модулю
по модулю 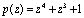 , на основе равенства (10). В таблице приведены значения остатков каждого разряда
, на основе равенства (10). В таблице приведены значения остатков каждого разряда
Значения остатков 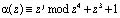
|
zj |
|
zj |
|
zj |
|
|
z0 |
1 |
z5 |
z3+z+1 |
z10 |
z3+z |
|
z1 |
z |
z6 |
z3+z2+z+1 |
z11 |
z3+z2+1 |
|
z2 |
z2 |
z7 |
z2+z+1 |
z12 |
z+1 |
|
z3 |
z3 |
z8 |
z3+z2+z |
z13 |
z2+z |
|
z4 |
z3+1 |
z9 |
z2+1 |
z14 |
z3+z2 |
Тогда, согласно (10), получаем остаток полинома 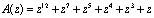
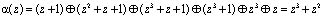 .
.
Таким образом, 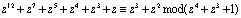 .
.
Второй обязательной немодульной операцией является обратное преобразование из кода ПСКВ в позиционный код [4]. Как правило, обратное преобразование из ПСКВ в ПСС выполняется на основе Китайской теоремы об остатках (КТО). Согласно этой теореме обратное преобразование определяется
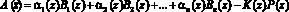 , (11)
, (11)
где 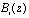 – ортогональный базис системы;
– ортогональный базис системы; 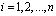 , K(z) – ранг, P(z) – полный диапазон.
, K(z) – ранг, P(z) – полный диапазон.
При этом ортогональный базис должен удовлетворять требованию
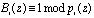 . (12)
. (12)
В работах [4-9] приведен алгоритм вычисления ортогональных базисов ПСКВ:
1. Вычисляется значение
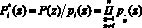 . (13)
. (13)
2. Определяется значение остатка
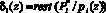 . (14)
. (14)
3. Выбирается вес ортогонального базиса
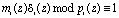 . (15)
. (15)
4. Вычисляется значение ортогонального базиса
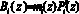 . (16)
. (16)
Вычислим ортогональные базисы ПСКВ, имеющей модули p1(z)=z+1, p2(z)=z2+z+1, p3(z)=z4+z3+z2+z+1, p4(z)=z4+z3+1, p5(z)=z4+z+1. Согласно выражений (13) и (14) имеем
|
P*1(z)= z14+z13+z12+z11+z10+z9+z8+z7+z6+z5+z4+ z3+z2+z+1; |
δ1(z)=1 |
|
P*2(z)= z13+z12+z10+z9+z7+z6+z4+z3+z+1; |
δ2(z)=z+1 |
|
P*3(z)= z11+z10+z6+z5+z+1; |
δ3(z)=z+1 |
|
P*4(z)= z11+z10+z9+z8+z6+z4+z3+1 |
δ4(z)=z+1 |
|
P*5(z)=z11+z8+z7+z5+z3+z2+z+1; |
δ5(z)=z3+1 |
Определим веса ортогональных базисов и их величины согласно (15) и (16):
|
m1(z)=1 |
B1(z)= z14+z13+z12+z11+z10+z9+z8+z7+z6+z5+z4+ z3+z2+z+1; |
|
m2(z)=z |
B2(z)= z14+z13+z11+z10+z8+z7+z5+z4+z2+z; |
|
m3(z)=z3+z |
B3(z)= z14+z13+z12+z11+z9+z8+z7+z6+z4+z3+z2+z; |
|
m4(z)=z3 |
B4(z)= z14+z13+z12+z11+z9+z7+z6+z3; |
|
m5(z)=z |
B5(z)=z12+z9+z8+z6+z4+z3+z2+z; |
Пусть задан полином
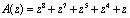 ,
,
который в ПСКВ имеет вид 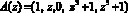 . Тогда обратное преобразование на основе КТО определяется (11)
. Тогда обратное преобразование на основе КТО определяется (11)
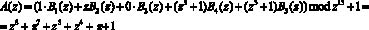
Приведенные в статье материалы и примеры позволяют сделать вывод о том, что полиномиальная система классов вычетов может быть использована при выполнении цифровой обработки сигналов на основе выражения
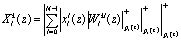 , (17)
, (17)
где 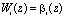 – первообразный элемент порядка d для локального кольца Pi(z), который задается модулем pi(z) ПСКВ; N – порядок мультипликативной группы, порожденной этим модулем; <<gonch53.wmf>>; l=1,2,…,m; k=0,1,…Т–1.
– первообразный элемент порядка d для локального кольца Pi(z), который задается модулем pi(z) ПСКВ; N – порядок мультипликативной группы, порожденной этим модулем; <<gonch53.wmf>>; l=1,2,…,m; k=0,1,…Т–1.
В этом случае структура непозиционного СП ЦОС, реализующего (17), имеет вид

Рис. 1. Структура параллельного спецпроцессора ПСКВ
Как наглядно видно из рис. 1, реализации ортогональных преобразований с использованием математической модели ЦОС в кольце полиномов будет задаваться выражением
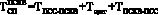 (18)
(18)
Характерной чертой непозиционного СП ЦОС является наличие n параллельных вычислительных трактов, которые функционируют независимо от друг от друга. В каждом из них реализуется ортогональные преобразования сигналов по соответствующему модулю. Распараллеливание на уровне операции позволяет отнести данный спецпроцессор к виду SIMD. Используя один поток команд, который одновременно поступает во все вычислительные тракты, вычислительное устройство реализует ортогональные преобразования согласно (17). Малоразрядность остатков, отсутствие обмена данных между вычислительными трактами, позволяет повысить производительность спецпроцессора по сравнению с классической архитектурой сигнальных процессоров. При этом для повышения точности вычислений достаточно увеличить число вычислительных трактов, т.е. увеличить число оснований ПСКВ.
Сравнительный анализ времени выполнения ортогональных преобразовании сигналов в позиционной системе (Т1) и с использованием параллельных вычислений (Т2) показан на рис. 2. Для оценки был выбран относительный коэффициент К=ТПСС/ТПСКВ.
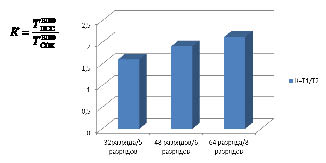
Рис. 2. Сравнительный анализ времени выполненияБПФ в ПСС (Т1) и в ПСКВ (Т2)
Анализ таблицы показывает, что применение ПСКВ позволяет повысить скорость цифровой обработки сигналов с использованием алгоритма БПФ более чем в 1,5 раза. Причем при увеличении разрядности обрабатываемых данных выигрыш возрастает. Так при обработке 64 разрядных данных скорость непозиционного процессора более чем в 2 раза превосходит скорость работы позиционного СП ЦОС, даже с учетом необходимости выполнения операций прямого и обратного преобразований кодов.
Заключение. В работе показана целесообразность использования параллельных вычислений для реализации ЦОС. Применение ПСКВ позволяет за счет независимой параллельной обработки малоразрядных остатков, позволяет сократить временные затраты на выполнение ортогональных преобразований сигналов по сравнению с позиционным спецпроцессором цифровой обработки сигналов.