Использование параллельных модулярных кодов позволяет повысить скорость обработки данных. Применение арифметики над малоразрядными остатками обеспечивает обработку информации в реальном масштабе времени. Дальнейшее повышение скорости цифровой обработки сигналов возможно за счет использования параллельной элементной базы, которая по своему характеру и организации вычислений совпадала с модулярными полиномиальными кодами
Среди непозиционных модулярных кодов особое место занимают модулярные полиномиальные коды (МПК). В данных кодах в качестве оснований системы используют неприводимые полиномы [1-5]. Обладая высокой скоростью обработки информации, такие коды нашли широкое применение в различных областях. Так в работах [1-3] показана реализация методов цифровой обработки сигналов (ЦОС) с использованием модулярного полиномиального кода. Малоразрядность остатков, выполнение вычислений по параллельным каналам, определяемых основаниями МПК, позволяют обеспечить цифровую обработку сигналов в реальном масштабе времени. Применения МПК в области защиты данных от несанкционированного доступа приведены в работах [4-6]. Использование кодов МПК позволяет повысить степень защиты данных от НСД за счет использования нелинейных алгоритмов зашифрования, которые базируются на операциях умножения и возведении в степень по модулю. Использование модулярных полиномиальных кодов для построения отказоустойчивых вычислительных систем ЦОС показано в работах [7-10]. Использование контрольных оснований позволяет разрабатывать эффективные алгоритмы поиска и коррекции ошибок, которые возникают в процессе функционирования специализированных процессоров из-за отказов и сбоев оборудования.
В основу всех данных реализаций положены математические основы построения полиномиальных непозиционных кодов. Если в качестве модулей алгебраической системы, на основе которой базируются модулярные полиномиальные коды, выбрать минимальные многочлены pi(z) поля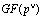 
, то любой полином A(z), удовлетворяющий условию 
где
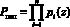, (1)
можно представить в виде n-мерного вектора
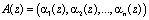, (2)
где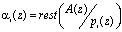 
, 
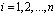
Рассмотрим выполнение арифметических операций в модулярном полиномиальном коде. Представим значения остатков операндов в виде полиномиальной записи.
Пусть степень минимального многочлена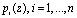 
, равна mi. Тогда остаток можно представить
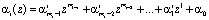. (3)
Соответственно для второго операнда получаем
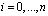. (4)
Так как сравнения по одному и тому же модулю можно почленно складывать, то для суммы двух полиномов A(z) и B(z), имеющих соответственно коды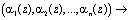 
и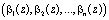 
справедливы соотношения:
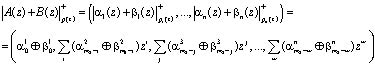, (5)
где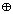 
– операция суммирования по модулю р.
Аналогично получаем для операции вычитания в МПК
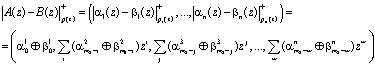, (6)
Следует отметить, что операция вычитания по модулю два совпадает с операцией суммирования по модулю 2.
Согласно (5) и (6) полученные подмножества по основаниям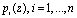 
МПК образуют циклическую группу сложения, которая содержит конечное число элементов. Операция сложения и обратная ей – вычитание производятся по модулю р, так как данные подмножества образуют аддитивную циклическую группу.
В силу дистрибутивности операции умножения операндов над кольцом на элементы этого кольца относительно операции сложения имеем
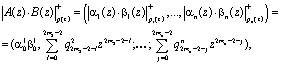(7)
где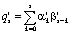 
– линейная свертка; 
;.
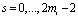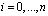Таким образом, выполнение операции умножения над операндами в расширенном поле Галуа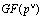 
согласно
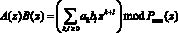, (8)
сводится к умножению соответствующих остатков по основаниям МПК с последующих суммированием по модулю характеристики поля.
Анализ выражений (5)-(8) показывает, что основным достоинством модулярных полиномиальных кодов является сравнительная простота выполнения модульных операций (сложения, вычитания, умножения). Рассмотренные выше формальные правила выполнения операций в МПК позволяют существенно повысить скорость вычислительных устройств. Так как основания системы представляют собой полиномы с небольшими степенями, то это позволяет использовать вычислительные устройства с заранее просчитанной детерминированной структурой.
Качественным скачком в обеспечении реального масштаба времени при реализации параллельных вычислений является использование нейросетевого логического базиса (НЛБ) [1-3]. Длительное время считалось, нейронные сети эффективны для решения так называемых трудноформализуемых и неформализуемых задач, связанных с необходимостью включения в алгоритм решения задач процесса обучения на реальном экспериментальном материале. В настоящее время к этому классу задач добавляется второй класс задач, не требующий обучения на экспериментальном материале, но хорошо представимый в нейросетевом логическом базисе. К ним относятся в первую очередь задачи с ярко выраженным параллелизмом – цифровая обработка сигналов и изображений в реальном масштабе времени [1-3]. Для этих задач переход к НЛБ обусловлен резким увеличением размерности пространства решения и необходимостью резкого уменьшения времени решения.
Основу нейросетевого логического базиса составляют операции типа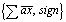 
, которые максимальным образом соответствуют логическому базису основных решаемых задач. Таким образом, соответствие базиса вычислительной системы и задачи обеспечивает максимальную производительность [1]. По общему признанию многих авторов это обусловлено, прежде всего, тем, что в основу параллельной работы НЛБ заложено внутреннее свойство большего массированного параллелизма.
Как наглядно видно из выражений (5)-(8) характерной чертой всех арифметических устройств, функционирующих в МПК, является необходимость выполнения операции суммирования по модулю два. Так как операция XOR нелинейная, то для ее решения используют классическую трехслойную нейронную сеть. Первый слой – входной слой содержит два формальных нейрона, которые не участвуют в процессе вычисления, однако осуществляют процесс распределения входного вектора х. Во втором слое располагаются два нейрона, а в выходном слое – один нейрон. Данная нейронная сеть относится к нейронным сетям прямого распространения и осуществляет выполнение операции суммирования по модулю два за 2 итерации, считая перераспределение входного вектора х на нейроны второго слоя. При этом синаптические веса между слоя образуют множество {–1, 1}.
Качественным скачком в решении данной проблемы является отказ от линейного вида функции активации и переход к нелинейному виду. Применение функции активации tribas (приведенной к треугольному виду) позволяет реализовать нейроподобный двухвходовой сумматор по модулю два на основе одного формального нейрона. На рисунке 1 показана структура сумматора по модулю два, реализованного в данном НЛБ.
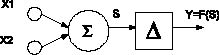
Рис. 1. Структура двухвходового сумматора по модулю два
Применение функции активации вида tribas обеспечивает значения сигналов
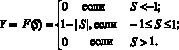(9)
Графически данная функция активация представлена на рис. 2.
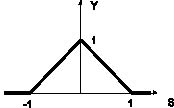
Рис. 2. Функция активации tribas
Исходные данные в двухмерном виде подаются на входы нейрона, умножаются на значения синаптических весов и поступают на сумматор, который реализует
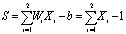, (10)
где S – выходной сигнал сумматора; Wi – весовые коэффициенты (равны единице); Xi – входные значения нейрона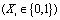 
; b = –1 – смещение.
С выхода сумматора полученное значение подается на схему активации, где и осуществляется разделение гиперкуба размерности n = 2 на два класса. Геометрическая интерпретация преобразования вводимых образцов под действием весовых коэффициентов, смещение и функции активации показана на рис. 3
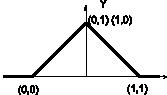
Рис. 3. Геометрическая интерпретация операции XOR с использованием функции активации tribas
Увеличение размерности входного вектора требует увеличения числа гиперплоскостей осуществляющих деление п-мерного гиперкуба на два класса. Пусть размерность гиперкуба n =3. Проблема моделирования отношения XOR для трехмерного входного вектора разделяющими плоскостями на рис. 4.
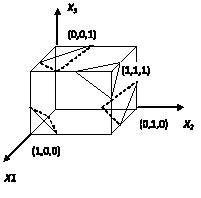
Рис. 4. Гиперплоскости, реализующие операцию XOR, для трехвходового нейроподобного сумматора
Из рис. 4 наглядно видно существование трех гиперплоскостей, осуществляющих разделение единичного гиперкуба на два класса:
– вершины у которых число единичных элементов равно единице;
– вершины у которых число единичных элементов отлично от единицы.
При этом данные гиперплоскости реализуются нейроном скрытого слоя, функционирующим согласно
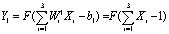. (11)
Однако выходной сигнал нейроподобного трехвходового сумматора по модулю два равен единице и в случае, когда число единичных элементов во входном векторе равно трем. Следовательно, необходим еще один нейрон, осуществляющий деление гиперкуба на два класса:
– вершины, у которых число единичных элементов равно трем;
– вершины, у которых число единичных элементов отлично от трех.
При этом данная гиперплоскость реализуется вторым нейроном скрытого слоя, функционирующим согласно
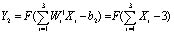. (12)
Таким образом, количество нейронов второго (скрытого) слоя равно двум, что определяется как
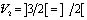. (13)
Для объединения информации об этих гиперплоскостях в выходном слое используется один нейрон с пороговой функцией активации, который осуществляет преобразование
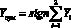. (14)
Обобщая сказанное, можно определить правила построения нейроподобного сумматора по модулю два:
– в качестве модели нейросетевого логического базиса выбран многослойный персептрон, семантические веса которого равны единице;
– входной слой содержит n нейронов (n – размерность входного слова), которые осуществляют приём и распределение сигналов на второй слой;
– скрытый слой содержит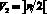 
нейронов с функцией активации tribas, осуществляющих разделение вершин гиперкуба гиперплоскостями на 2 класса, с чётным и нечётным числом единичных элементов, при этом смещение l-го нейрона равно 
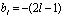, где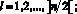 
– выходной слой содержит один нейрон пороговой функцией активации, используемый для объединения информации об этих гиперплоскостях.
Структура нейроподобного n-входового сумматора по модулю два показана на рисунке 5. Входной слой в процессе вычисления значения суммы по модулю два n-разрядного вектора не участвует, а осуществляет перераспределение данных, поступивших на входы нейронной сети. Скрытый слой содержит по одному нейрону для каждого возможного нечетного значения суммы элементов вектора входа, причем смещение нейрона равно значению возможной нечетной суммы со знаком минус. Синаптические веса между нейронами входного и срытого слоя равны 1. В качестве функции активации используем треугольную функцию активации. Выходной слой состоит из одного нейрона, синаптические веса входов которого равны 1, а смещение 0. В качестве функции активации используется пороговая функция.
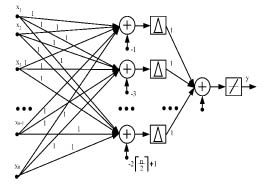
Рис. 5. Нейроподобный сумматора по модулю два
При этом число нейронов скрытого слоя составит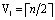 
, в то время как выходной слой содержит один нейрон V2 = 1. Тогда общее число нейронов равно
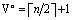. (15)
Применение трехслойной нейронной сети позволяет реализовать данную операцию за две итерации. Таким образом, очевидно, что достоинством данного метода построения многовходового нейросетевого сумматора по модулю два является высокое быстродействие при сравнительно небольших затратах оборудования.
В работе [1] показана возможность обучения нейронной сети с помощью генетических алгоритмов. Как показан в данной работе применение алгоритма обучения позволил обеспечить реализацию многовходового сумматора, который обладает меньшими аппаратными и временными затратами по сравнению с ранее рассмотренными.
Выводы. С целью повышения скорости обработки сигналов в современных вычислительных устройствах используют параллельные вычисления. Применение модулярного полиномиального кода позволяет осуществить распараллеливание на уровне операций. Дальнейшее повышение скорости обработки данных возможно за счет использования нейросетевого логического базиса. В работе приведена разработка многовходового нейросететвого сумматора по модулю два, который обладает минимальными временными и аппаратными затратами.