Одним из наиболее важных направлений развития научно-технического прогресса в сфере информатизации в настоящее время является микропроцессорная революция, для которой характерно широкое использование в системах обработки информации вычислительных систем (ВС), персональных компьютеров, микропроцессоров универсального и специального назначения. Основным направлением развития и совершенствования вычислительных устройств является неуклонный рост производительности и точности вычислений.
Существующая в последние годы в вычислительной технике тенденция к распараллеливанию вычислений связана с непрерывным ростом требований к производительности вычислительных средств. В принципе распараллеливание может быть осуществлено на нескольких уровнях:
• на уровне построения физических моделей объектов или процессов, создания математических моделей, позволяющих организовать параллельную обработку информации;
• на уровне метода решения;
• на уровне алгоритмов известных методов;
• на уровне программ;
• на уровне арифметических операций;
• на уровне обменов информации в ВС, ввода и вывода данных.
Одним из наиболее перспективных направлений в разработке высокоскоростных вычислительных систем является переход к распараллеливанию на уровне арифметических операций.
В современных и перспективных алгоритмах, использующих аппарат линейной алгебры, основными вычислительными процедурами являются операции типа перемножения векторов и матриц, обращение матриц, поиска собственных векторов и собственных значений матриц, решение систем линейных алгебраических уравнений. Данные процедуры линейной алгебры обладают повышенной вычислительной сложностью.
Качественным скачком в обеспечении реального масштаба времени и высокой точности вычислений является применение полиномиальной системы классов вычетов (ПСКВ), определяемой в расширенных полях Галуа GF(2v). Внутренний параллелизм, присущий арифметике ПСКВ, независимость обработки данных в вычислительных трактах, распараллеливание на уровне арифметических операций позволяют использовать перспективные принципы организации вычислительных систем [1-4].
Однако процессоры, составляющие значительную часть аппаратной реализации вычислительной техники, относятся к числу наименее надежных устройств, доля отказов и сбоев которых составляет более 50 процентов от общего числа отказов и сбоев аппаратуры. При этом среднее время ликвидации последствий последних, как правило, на 6-8 порядков превышает среднюю продолжительность выполнения задачи.
Таким образом, очевидна следующее противоречие: с одной стороны, постоянный рост требований к скоростным характеристикам вычислительных устройств приводит к необходимости организации параллельных вычислений, а с другой стороны, при этом увеличивается частота возникновения отказов, и возрастает время простоя, вызванное трудностью отыскания неисправности.
Наиболее перспективным путем разрешения данного противоречия является придание вычислительным системам свойства устойчивости к отказам в процессе функционирования. При этом fail-soft устойчивость к отказам (с амортизацией отказов) характеризует способность ВС обеспечивать обслуживание, несмотря на возникновение отказа, хотя и с понижением качества, то есть, находясь в состоянии постепенной деградации.
В работах [1-4, 8, 9, 10] показано, что полиномиальная система классов вычетов (ПСКВ) может быть использована при реализации цифровой обработки сигналов (ЦОС). Построение спецпроцессоров (СП) ЦОС, функционирующих в ПСКВ, позволяет обеспечивать обработку сигналов в реальном масштабе времени. Однако параллельная обработка информации в независимых вычислительных трактах позволяет не только повысить скорость обработки сигналов, но и может быть положена в основу построения корректирующих кодов ПСКВ [5-10].
Базисом в построении корректирующих кодов ПСКВ является распределение полиномов в полном диапазоне системы. В работе [2] показано, что в полиномиальной системе класса вычетов с основаниями 
в каждом интервале 
, где 
полного диапазона P(z) содержится по одному элементу последовательности .. В таблице приведен пример такого распределения для поля GF(23).
Распределение по диапазонам элементов 
|
A2,0 = (0,0,0) |
М2,0=0; |
A2,Z2= (0,z2,0) |
М2,Z2=z+1 |
|
A2,1= (0,1,0) |
М2,1=z2+1 |
A2,Z2+1= (0,z2+1,0) |
М2,Z2+1=z2+z |
|
A2,Z= (0,z,0) |
М2,Z=z2+z+1; |
A2,Z2+Z= (0,z2+z,0) |
М2,Z2+Z=z2 |
|
A2,Z+1=(0,z+1,0) |
М2,Z+1=z; |
A2,Z2+Z+1=(0,z2+z+1,0) |
М2,Z2+Z+1=1 |
Из таблицы наглядно видно что, каждый элемент 
последовательности лежит в своем диапазоне. При этом только один находится в нулевом интервале. Таким образом, если правильно подобрать количество рабочих и избыточных оснований, то можно обеспечить выполнение процедур поиска и коррекции ошибок.
При построении корректирующих кодов ПСКВ используют n оснований, из которых k являются информационными, а r – проверочными основаниями. Тогда полный диапазон
, (1)
разбивается на рабочий диапазон
и контрольный 
.
Многочлен A(z) с коэффициентами из поля GF(pv) будет считаться разрешенным в том и только том случае, если он является элементом нулевого интервала полного диапазона, то есть принадлежит рабочему диапазону. Если А(z) является элементом второго подмножества, то считается, что данная комбинация содержит ошибку. Таким образом, местоположение полинома А(z) относительно двух данных подмножеств позволяет однозначно определить, является ли кодовая комбинация разрешенной, или она содержит ошибочные символы. Характерной чертой избыточных кодов ПСКВ является их арифметичность, а так же равноправность информационной и избыточных частей кодограмм. При этом для выполнения процедур поиска и коррекции ошибок в кодах ПСКВ используются различные позиционные характеристики, алгоритмы вычисления которых приведены в работах [7-9].
Чтобы разработать структуру отказоустойчивого спецпроцессора ЦОС, функционирующего в ПСКВ, необходимо использовать методику, которая включает в себя следующие этапы.
На первом этапе решается задача, связанная с выбором пространственно-временного распределения реализуемого вычислительного процесса we из множества 
структурированных алгоритмов его решения.
. (2)
Второй этап методики посвящен вопросам выбора системы информационных и контрольных оснований ПСКВ. Математическая постановка задачи второго этапа имеет вид
, (3)
, (4)
где Vпскв – схемные затраты необходимые на реализацию спецпроцессора ПСКВ; Qпскв и Qдоп – точность обрабатываемых данных в модулярном коде и предельно допустимая точность; Nпскв и Nдоп – количество отказов, парируемых при обрабатываемых данных в модулярном коде, и предельно допустимое значение.
На третьем этапе проводится выбор алгоритма осуществляющего преобразование из позиционного кода в модулярный. Математическая постановка задачи имеет вид
(5)
где 
– j-й алгоритм прямого преобразования ПСС-ПСКВ, реализованный в нейросетевом базисе из S совокупности возможных алгоритмов; Тпсс-пскв – временные затраты на реализацию процедуры преобразований ПСС-ПСКВ.
На четвертом этапе выполняется выбор алгоритма преобразования ПСКВ-ПСС и его реализации базисе нейронной логики. Математическая постановка задачи имеет вид
(6)
где 
– l-й алгоритм преобразования ПСКВ-ПСС; Тпскв-псс – временные затраты на реализацию процедуры преобразований ПСКВ-ПСС.
На пятом этапе производится выбор позиционной характеристики для выполнения контроля и коррекции ошибок. Математическая постановка задачи, решаемой на данном этапе, имеет вид
, (7)
где 
– алгоритм коррекции ошибок в кодах ПСКВ; Vпсс – схемные затраты на ТМС СП ПСС; 
– суммарные схемные затраты на СП ПСКВ; Nдоп и 
– допустимое и парируемые отказы.
На шестом этапе решается задача определения стратегии реконфигурации СП ПСКВ известной структуры, обеспечивающей сохранение одного из показателей качества функционирования за счет снижения других показателей в заданных пределах при возникновении сбоев и отказов. Математическая постановка задачи имеет вид
, (8)
где 
– время и точность реализации ортогональных преобразований сигнала СП ПСКВ при реализации выбранного оа – го алгоритма реконфигурации; 
– совокупность возможных методов реконфигурации.
Проведем разработку структуры непозиционного спецпроцессора ЦОС, способного сохранять работоспособное состояние при возникновении потока отказов и сбоев за счет снижения в допустимых пределах основных показателей качества функционирования. В качестве исходных данных выбраны следующие параметры:
– частота дискретизации – 50 кГц;
– разрядность кодирования (входного слова) – 31 бит;
– минимально допустимая разрядность входного слова – 11 бит.
На первом шаге проводится анализ основных видов математических моделей цифровой обработки сигналов. В ходе анализа были рассмотрены дискретное преобразование Фурье (ДПФ)
, (9)
быстрое преобразование Фурье (БПФ) с прореживание по времени
, (10)
алгоритм Винограда для вычисления спектра сигнала
, (11)
а также теоретико-числовые преобразования (ТЧП)
, (12)
где М – число Мерсена над конечным полем Галуа 
; 
.
Особое место среди ортогональных преобразований сигналов является математическая модель ЦОС, реализованная в кольце полиномов
(13)
где 
.
Применение выражения (13) позволяет свести вычисление ортогональных преобразований сигналов в расширенном поле Галуа над кольцом Р(z) к n независимым вычислениям, проводимым по модулям pi(z) полиномиальной системы классов вычетов [3, 4, 7].
На втором шаге. Определяются основания и динамический диапазон обрабатываемых данных. В качестве рабочих модулей выступают полиномы
, 
,
,
.
В этом случае рабочий диапазон
.
Контрольными модулями являются 
, 
.
При этом аппаратурные затраты необходимые на реализацию (13) составят
, (14)
, (15)
где 
– количество оснований в ПСКВ.
Для выбора алгоритма прямого преобразования из позиционного кода в полиномиальную систему класса вычетов проведен анализ работ [1, 3, 4, 10], на основании которого выбран алгоритм непосредственного суммирования, который задается равенством
, (16)
где 
, 
.
В этом случае затраты для прямого преобразования ПСС в ПСКВ составят
. (17)
На четвертом этапе методики производится выбор алгоритма, реализующего обратное преобразование из модулярного кода в позиционный код. Проведенный анализ работ [3-5, 7] позволил выбрать алгоритм, базирующийся на основе китайской теоремы об остатках (КТО).
Согласно этой теореме обратное преобразование определяется
, (18)
где 
– ортогональный базис системы; 
, K(z) – ранг, P(z) – полный диапазон.
При этом ортогональный базис должен удовлетворять требованию
. (19)
На пятом этапе методики производится выбор позиционной характеристики, с помощью которой можно определить местоположение и глубину ошибки. На основе анализа работ [1, 2, 8-10] был выбран алгоритм параллельной нулевизации. В работе [6] приведена структура устройства, вычисляющего с помощью данного алгоритма позиционную характеристику – нормированный след полинома.
На последнем этапе методики для реализации метода реконфигурации целесообразно воспользоваться алгоритмом пересчета ортогональных базисов, реализованном на основе многослойной нейронной сети. Аппаратурные затраты на данную процедуру составляют
(20)
где ρ – разрядность сумматоров по модулю два.
Тогда вероятность безотказной работы нейросетевого СП ПСКВ будет определяться
, (21)
где
–
верояность безотказной работы подсети, реализующей ортогональное преобразование сигналов; 
и 
– вероятность безотказной работы устройства ПСС – ПСКВ и устройства перевода из ПСКВ в ПСС.
На рисунке приведены вероятности безотказной работы для спецпроцессора ДПФ, реализующего метод маскирования отказа «2 из 3», спецпроцессора ТЧП, реализующий метод «2 из 3» и СП ПСКВ с реконфигурируемой структурой.
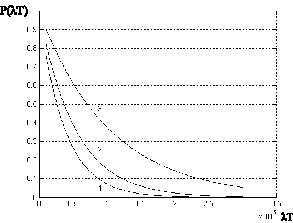
Вероятность безотказной работы СП ЦОС: 1 – СП ДПФ реализующий метод «2 из 3»; 2 – СП ТЧП реализующий метод «2 из 3»; 3 – СП ПСКВ с реконфигурируемой структурой
Анализ рисунка показывает, что применение полиномиальной системы классов вычетов для реализации цифровой обработки сигналов позволяет сохранять работоспособное состояние при возникновении потока отказов за счет деградации структуры СП и снижения в допустимых пределах основных показателей качества функционирования. При этом обеспечивается более высокая вероятность безотказной работы по сравнению с методом маскирования отказов «2 из 3».
Заключение. В работе приведена методика построения спецпроцессора ЦОС, реализация которой позволяет за счет применения корректирующих кодов ПСКВ и деградации его структуры обеспечить более высокую степень надежности функционирования по сравнению с классическим методом маскирования отказов «2 из 3». При этом СП сохраняет работоспособное состояние за счет снижения в допустимых пределах основных показателей качества функционирования.