Взаимосвязь теории с практикой была и остается одним из основных дидактических принципов естественнонаучного и инженерного образования. Его результативность подтверждается мировой педагогической практикой, а богатейший опыт человечества в использовании научных достижений при создании технических устройств и технологий, дает обширный предметный материал для формирования у студентов и курсантов умения применять теоретические знания в практических целях.
Изучив теорию конкретного процесса или явления – знания закономерностей протекания этого процесса или явления сконцентрированные человечеством на основании анализа и обобщения результатов всего предшествующего практического опыта, студент проверяет изученные законы на практике, прежде всего, решая учебные задачи, выполняя вычислительный, натурный и симулирующий компьютерный эксперимент. В естественнонаучных и инженерных науках преобладает прямая практическая проверка теоретических положений. Поэтому преподавание этих дисциплин невозможно без экспериментальной проверки изучаемого материала на натурных, виртуальных и компьютерных объектах.
В этой связи совершенствование форм и методов учебной экспериментально-практической и исследовательской деятельности в современном образовании является актуальной задачей. Откуда следует концепция настоящего исследования:
Стремительное обновление информационного пространства и современная информационная революция требуют адекватной и непрерывной модернизации учебного процесса преподавания естественнонаучных и инженерных дисциплин и, соответствующей этим дисциплинам, информационной среды учебной деятельности студентов, курсантов и преподавателей вузов.
Совершенствование методики и техники учебного эксперимента – важная составляющая модернизации информационной среды учебной деятельности, обеспечивающей формирование у студентов и курсантов умений и навыков исследовательской деятельности.
В статье представлены результаты работы по модернизации средств и методик проведения учебного вычислительного эксперимента в практике преподавания естественнонаучных и инженерных дисциплин, на примере совершенствования методики проведения электротехнического вычислительного эксперимента.
Цель исследования: модернизация средств и методик проведения учебного вычислительного эксперимента в практике преподавания естественнонаучных и инженерных дисциплин, на примере совершенствования методики проведения электротехнического вычислительного эксперимента
Материалы и методы исследования
Моделирование процесса обучения на основе использования современных компьютерных технологий, математическое моделирование, обобщение опыта.
Результаты исследования и их обсуждение
Первым шагом практической проверки изучаемой научной теории является решение учебной задачи – абстрактной проблемной ситуации, направленной на прогнозирование поведения некоторого умозрительного гипотетического объекта для вполне определенных и конкретных условий его эволюции. Чтобы прогнозировать поведение гипотетического объекта студенту необходимо:
• знать обобщенные математические модели элементов, входящих в структуру исследуемого в учебной задаче объекта;
• знать алгоритм использования обобщенных математических моделей структурных элементов, для составления математических моделей всего объекта;
• уметь составить математическую модель исследуемого объекта и рассчитать ее – т.е. уметь выполнить вычислительный эксперимент.
В практике преподавания естественнонаучных и инженерных дисциплин математические модели, исследуемые в учебных задачах, достаточно объемны и сложны, а их «ручная» математическая обработка требует больших затрат учебного времени, отводимого на аудиторную и самостоятельную работу студента.
С целью оптимизации использования учебного времени студентов, необходимо научить их использованию возможностей современных программно-аппаратных средств, чтобы на этой основе минимизировать временные затраты на вычислительные операции.
В учебном процессе естественнонаучных и инженерных дисциплин нет избытка времени, позволяющего изучать прикладные программы со сложным интерфейсом. В этой связи, среди большого количества современных программных продуктов, используемых для проведения вычислительного эксперимента, особого внимания заслуживает пакет Mathematica – мощная система компьютерной алгебры с достаточно удобным, интуитивно понятным и простым в освоении интерфейсом.
Mathematica является ведущим программным продуктом для обработки числовых, символьных и графических данных, повсюду используемым профессионалами практически в каждой ветви научных и технических вычислений. Mathematica обходится механизмами математики, поэтому пользуясь ею, студенты могут концентрироваться на содержании и смысле своей работы.
Учебные учреждения всего мира используют пакет Mathematica в университетском образовании. Однако сразу следует отметить высокую стоимость пакета Mathematica, что делает весьма проблематичным его использование российскими студентами. Потому в нашей работе исследуются возможности применения в учебном вычислительном эксперименте альтернативных, свободных систем компьютерной математики.
В этой связи, нами, в рамках госбюджетной научно-исследовательской работе по теме 7.16/09 «Совершенствование методики и техники учебного электротехнического эксперимента», выполняемой на кафедре Электрооборудования судов в Мурманском Государственном техническом университете, был проведен сравнительный анализ возможностей использования в учебном вычислительном эксперименте ряда альтернативных, свободных систем компьютерной математики.
Для исследования возможности использования альтернативных бесплатных систем компьютерной алгебры в вычислительном электротехническом эксперименте еще во время первого этапа ГБ НИР были сформированы студенческие творческие коллективы (СТК), выполнившие сравнительный анализ возможностей использования в учебном процессе пакетов символьной математики Maxima, Scilab, Axiom и Matlab.
По результатам первого этапа мы остановили свой выбор на пакете Scilab, поскольку сочли его интерфейс наиболее удобным.
Интерфейс этого пакета близок к интерфейсу пакета Mathematica. Основное отличие состоит в том, что Scilab предполагает исключительно строчный способ записи математических выражений и команд. Mathematica позволяет более наглядно и привычно вводить в программу информацию: можно использовать надстрочные символы при возведении переменной в степень, пакет допускает запись подстрочных индексов, символов интеграла, корней любой степени, запись матриц с отображением столбцов и строк.
Наша педагогическая практика показала, что свободно распространяемый пакет символьной математики Scilab обладает рядом достоинств, основными из которых являются:
• удобный интерфейс, в основе которого интегрированный в Scilab текстовый блокнот, позволяющий передавать текст программы, написанной в блокноте, в командное окно – с целью ее исполнения;
• возможность выполнения символьных вычислений, позволяющих минимизировать время на ввод начальных условий и математической модели, исследуемой в вычислительном эксперименте;
• простой язык программирования, очень близкий естественному математическому языку, что минимизирует время на обучение студентов применению этого пакета для решения конкретных учебных задач вычислительного эксперимента;
• широкие возможности матричных вычислений, широкие графические возможности представления результатов вычислительного эксперимента.
Применение пакета Scilab дает возможность подготовить студентов к выполнению натурного исследования реального процесса или явления в естественных или лабораторных условиях и получить практическое подтверждение работоспособности полученных ими теоретических знаний. Обработка результатов натурного эксперимента в среде пакета Scilab также очень эффективна.
Продемонстрируем возможности использования пакета Scilab для решения электротехнических задач с помощью символьных вычислений, с использованием собственного текстового блокнота программы. В качестве примера выполним расчет токов мостовой ЛЭЦ постоянного тока изображенной на рис. 1(а).
Параметры элементов этой цепи известны: R1 = 150 Ом, R2 = 100 Ом, R3 = 200 Ом, R4 = 150 Ом, R5 = 250 Ом, R6 = 50 Ом, E1 = 220 В, E2 = 200 В.
Решим задачу методом контурных токов.
На рис. 1(б) для исходной схемы выбрана система из трех контуров, которыми задействованы все электрические ветви исследуемой цепи. Там же для каждой из ветвей показаны, выбранные нами произвольно, положительные направления токов в ветвях.
а б
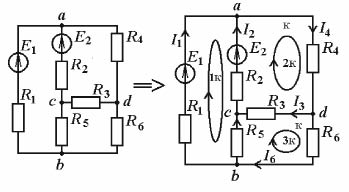
Рис. 1. Приведение исходной схемы исследуемой электрической цепи к расчетной схеме, основанной на методе контурных токов (МКТ): а – принципиальная электрическая схема исследуемой цепи; б – расчетная схема исследуемой цепи, основанная на МКТ
Математическая модель цепи, составленная на основе метода контурных токов, имеет в матричной форме следующий вид:
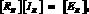
произведение матрицы контурных сопротивлений на матрицу контурных токов дает матрицу контурных ЭДС.
Матрица контурных сопротивлений имеет вид:
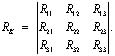
Рассчитаем коэффициенты этой матрицы. Коэффициенты главной диагонали:
R11 = R1 + R2 + R5; R22 = R2 + R3 + R4;
R33 = R3 + R5 + R6;
Коэффициенты, расположенные вне главной диагонали:
R12 = R21 = – R2; R13 = R31 = – R5;
R23 = R32 = – R3;
Рассчитаем коэффициенты матрицы контурных ЭДС:
E11 = E1 – E2; E22 = E2; E33 = 0;
Введем в окно блокнота SciNotes (см. рис. 2), интегрированного в Scilab, исходные данные задачи, формулы для расчета числовых коэффициентов матриц и программный код для решения матричного уравнения.
Обратим внимание на некоторые особенности синтаксиса языка пакета Scilab:
Если строка начинается двумя слешами «//», то все записи, следующие за слешами в этой строке, программой не исполняются. Т.е. два слеша – это команда, объявляющая начало следования пользовательского пояснения – ремарки. Блокнот программы Scilab автоматически расцвечивает ремарки в файле-сценарии зеленым цветом. На рис. 2 это строки с номерами 1, 3, 5, 7, 9, 11, 13, 15.
Scilab, обрабатывая очередную командную строку, прочитанную из файла-сценария, сначала выводит ее в командное окно, где она начинает исчисляться. Результат исчисления очередной команды будет выведен в командном окне только в том случае, если команда не закрыта символом точка с запятой «;». На рис. 2 этим символом закрыты все выражения строк с номерами 2, 4, 6 10, 12. Исключение составляет применение этого символа для объявления конца очередной (но не последней) строки матрицы.
Все команды программы Scilab записываются малыми латинскими буквами. Если команда написана в файле-сценарии верно, Scilab расцвечивает ее цветом.
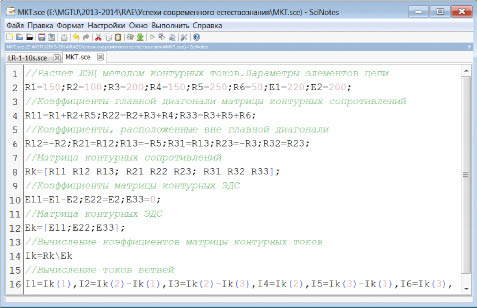
Рис. 2. Вид окна SciNotes-блокнота, в который записан файл-сценарий с программным кодом решения задачи
Матрица элементов с обеих сторон ограничивается квадратными скобками. Коэффициенты матрицы расположенные в одной строке разделяются пробелами, в конце каждой строки (исключая последнюю) ставится точка с запятой, после которой следует очередная строка матрицы. Например, в строке 8 файла-сценария, приведенного на рис. 2, переменная Rk объявляется в качестве имени матрицы. Матрице Rk (с помощью знака равенства) присвоены числовые значения ее коэффициентов, приведенные в квадратных скобках. Матрица Rk – квадратная, она содержит 3 строки, в каждой из которых по 3 числовых коэффициента. В 12-й строке файла сценария аналогичным образом объявлена прямоугольная матрица Ek – матрица контурных ЭДС, содержащая 3 строки и один столбец.
Особого внимания заслуживает команда «левого деления», использованная в 14-й строке программного кода. Она записывается с помощью символа «\» (с помощью обратного слеша). С помощью этой команды матрица контурных сопротивлений левым делением делится на матрицу контурных ЭДС. Результат этой операции – матрица искомых контурных токов. Таким образом, команда левого деления – это возможность краткой записи сложной процедуры. С помощью команды левого деления в программе Scilab вызывается подпрограмма транспонирования матрицы контурных сопротивлений и последующего деления матрицы контурных ЭДС на транспонированную матрицу.
На рис. 3 приведен вид командного окна с результатами исчисления.
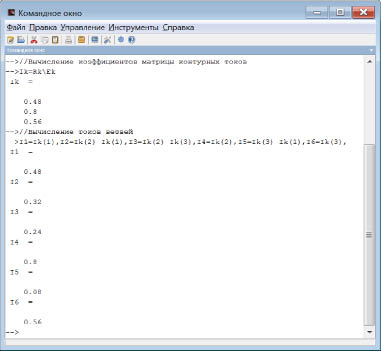
Рис. 3. Вид командного окна с результатами исчисления
Для организации консультаций студентам по использованию пакета Scilab в учебном вычислительном эксперименте был организован учебный сайт (http://af-toe-mgtu.ucoz.ru/), на одной из страниц которого мы выкладываем методические материалы в помощь студентам и курсантам университета, использующим этот пакет. Еще одна страница этого сайта – учебный видео-лекторий, пока нами создано только одно учебное видео.
Заключение
Использование свободно распространяемого пакета Scilab в учебном вычислительном эксперименте естественнонаучных и инженерных дисциплин целесообразно по ряду соображений.
Потенциал предметного содержания естественнонаучных и инженерных дисциплин может быть реализован, при условии активной познавательной деятельности курсантов и студентов по освоению изучаемой дисциплины.
Продуктивное усвоение студентами и курсантами предметного материала дисциплины на основе учебного вычислительного эксперимента определяет мотивационный аспект, формирует познавательный интерес и ценностное отношение к профессиональным знаниям.
Наряду с мотивационным аспектом, практико-ориентированное обучение естественнонаучным и инженерным дисциплинам обеспечивает инженерному образованию содержательный и процессуальный аспекты.
Освоение естественнонаучных и инженерных дисциплин способствует развитию физического понимания процессов, протекающих в изучаемых технических устройствах, осмыслению и более глубокому усвоению знаний, необходимых для профессиональной деятельности инженера, умению прогнозировать явления, происходящие в изучаемых технических объектах, конструировать новые технические устройства с заданными функциональными свойствами.



