В большинстве случаев при прогнозировании осадок оснований сооружений возникает необходимость одновременного учета свойства консолидации, ползучести и старения скелета грунта. При этом старение грунта является результатом уплотнения его под действием внешней нагрузки, а также проявления сцепления упрочнения, обусловленного протеканием во времени физико-химических процессов на контактах твердых и жидких фаз. Его интенсивность зависит от целого ряда факторов и, в первую очередь, от водосодержания.
Старение грунта математически можно описать различными алгебраическими выражениями. При этом, учитывая, что деформации ползучести зависят от возраста уплотняемого грунта в момент приложения нагрузки t и продолжительности действия нагрузки t – t согласно [1] за меру ползучести можно принять:
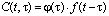 , (1)
, (1)
где
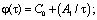
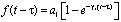 ; (2)
; (2)
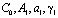 – экспериментальные данные.
– экспериментальные данные.
Для решения задач механики уплотняемых пористых сред согласно основной модели В.А. Флорина [6], (На основе этой модели решены некоторые задачи в работах [2-4], [7]), необходимо совместно рассматривать уравнения, отражающие неразрывность твердой и жидкой фаз грунта, состояние его скелета, а также условия равновесия нестабилизированного состояния уплотняемого грунтового массива, т.е.
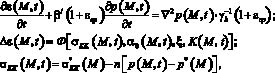 (3)
(3)
где
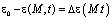 ;
;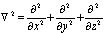 ;
;
Ф – функция, отражающая напряженно-деформированное состояние скелета грунта; e(М,t) – коэффициент пористости уплотняемого грунта для исследуемой точки M в момент времени t; β1 – коэффициент объемного сжатия; eср – средний коэффициент пористости; p – давление в поровой жидкости; γb – объемный вес воды; ε0 – начальный коэффициент пористости; 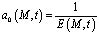 – коэффициент сжимаемости грунта;
– коэффициент сжимаемости грунта; 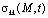 – сумма главных напряжений; n – размерность рассматриваемой задачи; x – коэффициент бокового давления уплотняемого грунтового массива;
– сумма главных напряжений; n – размерность рассматриваемой задачи; x – коэффициент бокового давления уплотняемого грунтового массива; 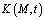 – величина, которая учитывает вязкие свойства уплотняемого грунта и она зависит от выбранной математической модели состояния грунта;
– величина, которая учитывает вязкие свойства уплотняемого грунта и она зависит от выбранной математической модели состояния грунта; 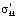 , p* – сумма главных напряжений и давление в поровой жидкости для стабилизированного состояния уплотняемого грунтового массива; x,y,z – координаты точки M.
, p* – сумма главных напряжений и давление в поровой жидкости для стабилизированного состояния уплотняемого грунтового массива; x,y,z – координаты точки M.
Механика многокомпонентных сред, основываясь на экспериментальные исследования, развивалась в нескольких направлениях. В настоящее время основными из них являются составление уравнений состояния фаз грунта; установление характера взаимодействия твердых частиц вместе с жидкостью и газом, заполняющих их поры; решения краевых задач для оценки НДС уплотняемых массивов, находящихся под действием поверхностных и объемных сил.
Эти задачи механики многофазных сред взаимно связаны, и успешное решение их зависит от решения каждой из них в отдельности. Причем первые два направления имеют принципиальное значение при рассмотрении задач механики уплотняемых пористых грунтов, и в зависимости от принятой модели многофазного деформируемого тела приходим к различным вопросам ее краевых задач. Следовательно, определение НДС грунтового массива зависит от удачного математического описания его в процессе деформирования. Если между компонентами деформации и напряжений скелета упругоползучего грунта примем линейную зависимость, то второе выражение системы формул (3) примет вид:
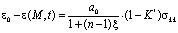 . (4)
. (4)
Здесь
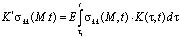
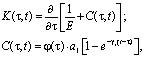 (5)
(5)
где j – функция старения, зависящая от физико-механических свойств уплотняемого грунта; a1, γ1 – параметры ползучести; ε0 – начальный коэффициент пористости; x, n – коэффициенты соответственно бокового давления и Пуассона; 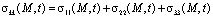 – сумма главных напряжений. При упругой уплотняемой однородной среде соотношение (4) имеет вид
– сумма главных напряжений. При упругой уплотняемой однородной среде соотношение (4) имеет вид
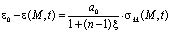 .
.
Исследования системы уравнений (3) при (4) и (5) приводят к изучению уравнения вида
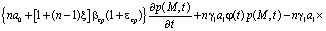
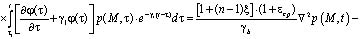
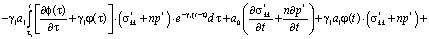
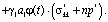 (6)
(6)
Выражение (6) является интегро-дифференциальным уравнением и его решение при соответствующих краевых условиях дает возможность определить распределение давлений в поровой жидкости. Это уравнение можно привести к дифференциальному уравнению второго порядка. Для этого (6) продифференцируем по t, затем полученное сложим с (6) предварительно умножив его на γ1. В результате имеем:
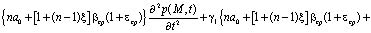
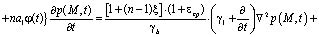
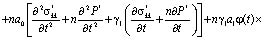
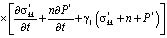 . (7)
. (7)
Выражение (7) является основным уравнением механики многофазных наследственно-стареющих уплотняемых грунтов. Откуда при bср=0 находим уравнение уплотнения водонасыщенного грунта, т.е.
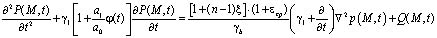 , (8)
, (8)
где
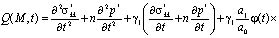
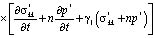 . (9)
. (9)
Таким образом, получены уравнения механики наследственно – стареющих грунтов при их линейном деформировании. В дальнейшем они будут решены для различных задач уплотнения, имеющие теоретическое и практическое значение в механике уплотняемых пористых сред.
Для того чтобы сформулировать краевые условия, введем некоторую область трехмерного Евклидового пространства Е3, где происходит процесс уплотнения (консолидации), т.е. G – область изменения пространственных переменных xi, i=1,2,3, а Е3 – совокупность точек, координаты которой определяются тремя этими действительными числами. Пусть Г – граница области, которая должна быть кусочно-гладкой поверхностью, состоящей из конечного числа гладких кусков, а W – некоторая область в четырехмерном пространстве W = G*(t,Т); 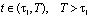 . Ее граница состоит из боковой поверхности Гб = Г×[
. Ее граница состоит из боковой поверхности Гб = Г×[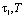 ] и двух оснований: нижнего М∈G, t = τ1 и верхнего М∈G, t = Т. Иными словами, область W является областью задания уравнений уплотнения, G – область, соответствующая геометрической форме и размеру уплотняемого тела, в котором изучается процесс уплотнения, а Г – область задания граничных условий.
] и двух оснований: нижнего М∈G, t = τ1 и верхнего М∈G, t = Т. Иными словами, область W является областью задания уравнений уплотнения, G – область, соответствующая геометрической форме и размеру уплотняемого тела, в котором изучается процесс уплотнения, а Г – область задания граничных условий.
Так как основное уравнение механики уплотняемых наследственно – стареющих грунтов представлено в виде дифференциального уравнения второго порядка относительно порового давления, то для определения единственного его решения необходимо знать два начальных условия. Одно из них является задание во всех точках области в момент t = τ1 самой функции, т.е.
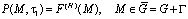 , (10)
, (10)
где функция F(H)(M) непрерывна в точках области G. Эта область есть объединение множества G и его границы Г. В случае одномерной задачи уплотнения грунтов начальное условие упрощается и имеет вид:
для двухфазной и трехфазной сред соответственно
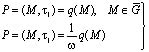 , (11)
, (11)
где коэффициент w учитывает объемное сжатие грунта за счет газообразных составляющих. В остальных случаях необходимо решать уравнения фильтрации при соответствующих граничных условиях. Другое начальное условие может быть найдено из уравнения (6) учитывая, что при t = τ1 искомое решение должно удовлетворять ему. При этом имеем
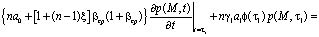
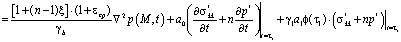 . (12)
. (12)
В математической теории уплотнения земляных масс можно встретить три основных разновидностей граничных условий.
Первые два условия в общем виде можно представить следующим образом:
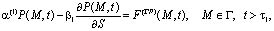 (13)
(13)
где 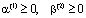 .
.
Если 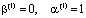 , то имеем первую краевую задачу. В этом случае для любого момента времени задается распределение порового давления или напора на граничной поверхности, а следовательно, и напряжения в скелете грунта. В частности, если жидкость свободно удаляется с некоторой части контура Г уплотняемой среды, то напор или давление на ней равно нулю, т.е.
, то имеем первую краевую задачу. В этом случае для любого момента времени задается распределение порового давления или напора на граничной поверхности, а следовательно, и напряжения в скелете грунта. В частности, если жидкость свободно удаляется с некоторой части контура Г уплотняемой среды, то напор или давление на ней равно нулю, т.е.
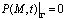 .
.
Если же в (13) примем a(1) = 0, b(1) = К (К – коэффициент фильтрации), то имеем второе граничное условие. В этом случае для каждой точки поверхности уплотняемого тела должен быть задан поток жидкости как функции пространственных координат и времени
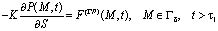 ,(14)
,(14)
где S – нормаль к поверхности Г в точке М.
Кроме указанных условий при изучении отдельных задач механики твердого деформируемого тела, можно столкнуться с граничными условиями сопряжения. Эти условия обычно используются в случае контакта нескольких различных тел. В теории уплотнения они применяются при определении НДС многослойных грунтовых оснований.
Таким образом, основное уравнение механики уплотняемых пористых наследственно – стареющих грунтов, полученные в виде (8) связывает временно – пространственное распределение порового давления внутри исследуемого массива. Чтобы найти его, необходимо знать распределение давлений в поровой жидкости внутри уплотняемого тела в начальный момент времени, геометрическую форму и размеры тела, закон фильтрующей поверхности его между окружающей средой (граничное условие).
Следовательно, при введенных выше обозначениях, краевые задачи уравнения механики уплотняемых наследственно-стареющих грунтов формулируются следующим образом: требуется определить в области W дважды непрерывно дифференцируемое по пространственным координатам, непрерывно дифференцируемое по времени второго порядка и непрерывное вплоть до границы решение P(M,t) или σkk(M,t) уравнений (8), удовлетворяющее соответствующим краевым условиям исследуемых задач.
На основе такой постановки задач теории консолидации и ползучести можно исследовать ряд их вопросов одномерного и многомерного уплотнения, решения которых можно представить в виде комбинации функции Куммера. Задача в одномерной постановке ранее исследована в [5].
Грунт в общем случае находится в сложном НДС, вызванном воздействием внешних нагрузок, передающихся через фундамент и силами собственного веса, т.е. имеет место пространственное сжатие грунта. Однако в инженерной практике часто создаются условия, когда такое состояние уплотняемого массива многокомпонентного грунта сводится к одномерной задаче. К таким случаям относятся уплотнения грунтовых массивов и слоев в основании сооружений, имеющих большие размеры по сравнению с их мощностью.
При одномерном уплотнении элементарный кубик, выделенный из массива грунта деформируется в условиях отсутствия бокового расширения. Причем направление сжимаемости кубика-образца совпадает с направлением действия наибольшего главного напряжения. В двух других направлениях деформации равны нулю. В этих условиях относительная деформация уплотнения равна относительной объемной деформации грунта.
Для выяснения общего характера протекания процесса уплотнения достаточно будет рассмотреть отдельные решения именно этой задачи, физическая сторона которой не очень отличается от аналогичных решений трехмерных задач. С другой стороны, исследования одномерного уплотнения более доступны, чем двух и трехмерных. Кроме того, это дает возможность при рассмотрении процесса уплотнения учесть некоторые факторы, сильно влияющие на него, в частности, можно указать на одновременный учет неоднородности, старения и ползучести уплотняемых грунтов. В связи с этим можно исследовать процесс одномерного уплотнения, происходящий в слое трехфазного грунта для ряда задач механики.
Пусть слой грунта мощностью h в момент времени 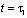 подвержен действию внешней распределенной нагрузки с интенсивностью
подвержен действию внешней распределенной нагрузки с интенсивностью 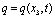 . Верхняя поверхность уплотняемого массива водопроницаема, а нижняя водонепроницаемая.
. Верхняя поверхность уплотняемого массива водопроницаема, а нижняя водонепроницаемая.
При этом основное уравнение одномерной задачи механики однородных уплотняемых наследственно-стареющих трехфазных грунтов находим из (8), приняв n =1, 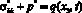 . Это уравнение в безразмерных координатах имеет вид:
. Это уравнение в безразмерных координатах имеет вид:
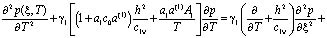
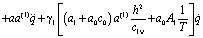 , (15)
, (15)
где
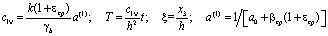 . (16)
. (16)
Начальными условиями для данной задачи, согласно (11) и (12) будут:
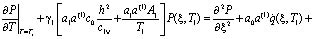
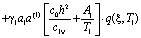 ; (17)
; (17)
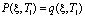 . (18)
. (18)
Граничные условия (13) запишутся так:
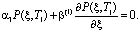 (19)
(19)
Причем, согласно условию задачи, при x =0 имеет место 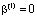 и при
и при 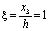 ,
, 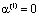 .
.
Таким образом, данную задачу можно сформулировать следующим образом. В безразмерных координатах требуется определить давление в поровой жидкости 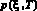 , напряжение в скелете s(x,T) и вертикальные перемещения верхней поверхности S(T) (осадок) грунтового слоя в области
, напряжение в скелете s(x,T) и вертикальные перемещения верхней поверхности S(T) (осадок) грунтового слоя в области 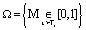 , если p(x,T) удовлетворяет дифференциальному уравнению (15) начальным (17), (18) и граничным (19) условиям.
, если p(x,T) удовлетворяет дифференциальному уравнению (15) начальным (17), (18) и граничным (19) условиям.
Если рассмотрим процесс уплотнения в слое стареющего трехфазного упругоползучего грунта с водоупором на глубине h, ограниченном с боков водонепроницаемыми стенками, и находящимся под действием равномерно распределенной нагрузки q, приложенной на участке (–a, a) поверхности массива, то его исследование сводится к решению следующей краевой задачи теории консолидации грунтов: требуется определить непрерывную функцию р(M,t), удовлетворяющую в области 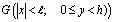 уравнению
уравнению
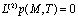 (20)
(20)
начальным
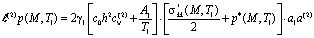 , (21)
, (21)
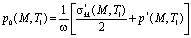 (22)
(22)
и граничным
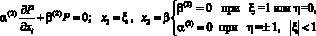 (23)
(23)
условиям. Здесь L(2) – дифференциальный оператор вида
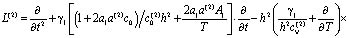
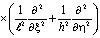 , (24)
, (24)
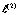 – оператор вида
– оператор вида
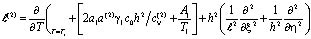 , (25)
, (25)
Данная краевая задача (20) –(25) дает возможность определить давление в поровой жидкости, представленное в безразмерных координатах. Все эти выражения получены из (8) и (12), причем начальное распределение порового давления для трехфазной среды имеет вид:
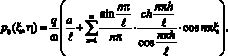 (26)
(26)
Следует заметить, что решения всех этих задач (15)-(26) теории консолидации наследственно-стареющих грунтовых сред представляются в виде комбинации вырожденных гипергеометрических функции первого и второго родов 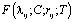 ,
, 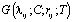 . При этом
. При этом 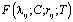 называется функцией Куммера. Она разлагается в степенной ряд, сходящийся при всех
называется функцией Куммера. Она разлагается в степенной ряд, сходящийся при всех 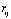 ,т.е.
,т.е.
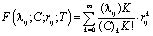 , (27)
, (27)
где 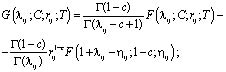 (28)
(28)
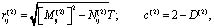
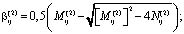
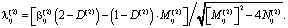
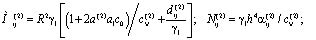
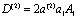 .
.
Во всех полученных решениях, представленных в виде комбинации функции Куммера (27) и (28) скорость консолидации зависит от безразмерных параметров 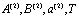 , которые в свою очередь зависят от параметров
, которые в свою очередь зависят от параметров 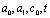 , определяемые по результатам компрессионных испытаний грунтов, которые для различных глинистых пород в основном имеются.
, определяемые по результатам компрессионных испытаний грунтов, которые для различных глинистых пород в основном имеются.



