При консолидации глинистого грунта из-за низкой его водопроницаемости затрудняется отток воды, выжимаемой из пор. Поэтому некоторая часть напряжений воспринимается водой, содержащейся в порах, что приводит к образованию порового давления. Поскольку сами напряжения в различных точках грунтового основания неодинаковы, то в них будут различны и величины порового давления.
Во многих случаях деформация уплотнения является одной из существенных частей общей деформации. Поэтому разработка вопросов уплотнения имеет весьма большое значение в механике грунтов и ее приложениях к гидросооружениям. В частности, при исследованиях уплотнений ядер или экранов высоких плотин смешанного типа, выполняемых из связного грунта, изучение вопросов устойчивости откосов земляных сооружений или оснований крупнейших промышленно – гражданских, гидротехнических и мелиоративных сооружений при нестабилизированном состоянии грунта и т.п.
Во всех выше перечисленных случаях, исследование процесса уплотнения сводится к изучению изменения во времени дополнительных давлений в воде (или напора) и напряжений в скелете грунта, вызванных приложением той или иной уплотняющей нагрузки [2-4, 7].
В целом, при возведении сооружения, под действием нагрузок, передаваемых от него основанию, происходит консолидация грунтов. Благодаря чему, сопротивление сдвигу грунтов основания возрастает. Причем устойчивость гидротехнического и крупнопромышленных сооружений на глинистых грунтовых основаниях во многом зависит от сопротивления грунта сдвигу. Однако из-за замедленности процесса консолидации нарастание сопротивления сдвигу происходит медленно и обычно не заканчивается в период ввода сооружения в эксплуатацию, что может отрицательно повлиять на устойчивость сооружений и в последующем в период эксплуатации. Причем сам процесс уплотнения относится к многомерным задачам теории консолидации и ползучести многофазных грунтов [5].
В связи с этим ниже решим задачу теории консолидации земляных масс применительно к уплотнению слоя упругоползучего грунта с учетом его свойства старения. Для этого рассмотрим грунтовой массив в виде параллелепипеда с водоупором на глубине h и с водонепроницаемыми стенками на 2l1 и 2l2, находящегося под действием равномерно распределенной нагрузки с интенсивностью q, приложенной на части поверхности этого параллелепипеда со сторонами 2а и 2b. Применительно к этой схеме исследуемую задачу сформулируем так: требуется найти непрерывную функцию, отражающую изменение давлений в поровой жидкости и удовлетворяющую в области
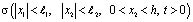
дифференциальному уравнению вида
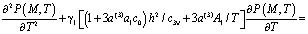
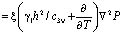 (1)
(1)
начальным
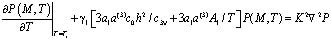 +
+
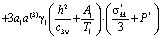 (2)
(2)
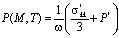 , (3)
, (3)
и граничным
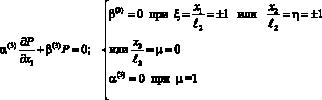 (4)
(4)
условиям, соответствующим для исследуемой задачи. Здесь все величины записаны относительно безразмерных координат и
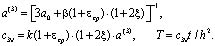 (5)
(5)
Кроме этих условий в силу симметрии, функция P(x,h,m) должна быть четной относительно x и h в отдель ности.
Начальное распределение порового давления в слое исследуемого массива для трехфазной земляной массы относительно безразмерных координат имеет вид:
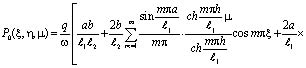
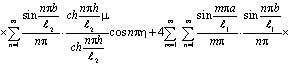
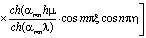 . (6)
. (6)
Здесь при выводе равенства (1) и (2) в качестве уравнения состояния упругоползучих однородных грунтов принято выражение вида:
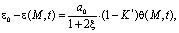 (7)
(7)
где
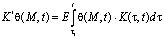 ; (8)
; (8)
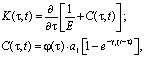 (9)
(9)
где j – функция старения, зависящая от физико-механических свойств уплотняемого грунта; a1, γ1 – параметры ползучести; ε0 – начальный коэффициент пористости; x – коэффициент бокового давления; e(М,t) – коэффициент пористости для исследуемого момента времени t; Е – модуль общей деформации уплотняемого грунта; a0 – коэффициент сжимаемости грунта; q(M,t) – сумма главных напря жений.
Уравнение, отражающее неразрывность твердой и жидкой фаз грунта согласно [1] принято в виде:
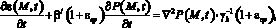 (10)
(10)
где 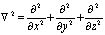 ; β1 – коэффициент объемного сжатия; eср – средний коэффициент пористости; Р(М,t) – давление в поровой жидкости; γb – объемный вес воды.
; β1 – коэффициент объемного сжатия; eср – средний коэффициент пористости; Р(М,t) – давление в поровой жидкости; γb – объемный вес воды.
Условие равновесия нестабилизированного состояния уплотняемого грунтового массива, согласно основной модели В.А. Флорина[6] имеет вид:
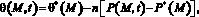 (11)
(11)
Здесь q*, P* – сумма главных напряжений и давление в поровой жидкости для стабилизированного состояния уплотняемого грунтового массива; x,y,z – координаты точки M.
Совместно рассматривая выражения (7)-(11) в безразмерных координатах получим (1)-(3). Решим эту систему уравнений применительно к граничным условиям (4). Причем выражение (6) является решением исследуемой задачи, соответствующим начальному моменту времени. Оно определено в безразмерных координатах как решение уравнения Лапласа, удовлетворяющее граничным условиям задачи.
Решение уравнения (1), удовлетворяющее граничным условиям (4), получим в виде:
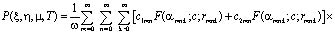
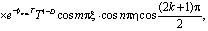 (12)
(12)
где 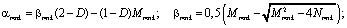
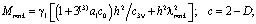
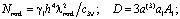
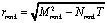
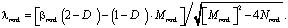 (13)
(13)
Здесь произвольные постоянные c1mnk и c2mnk находятся из начальных условий (2) и (3). Использовав их, имеем:
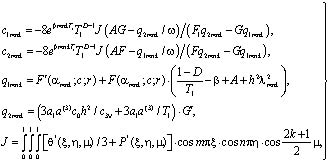 (14)
(14)
где функции F(αmnk;c; rmnk) и G(αmnk;c; rmnk) являются частными решениями вырожденного гипергеометрического уравнения относительно переменной 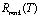
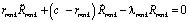 . (15)
. (15)
Причем частные решения уравнения (15) 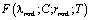 и
и 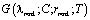 называются вырожденными гипергеометрическими функциями первого и второго родов. При этом
называются вырожденными гипергеометрическими функциями первого и второго родов. При этом 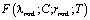 называется функцией Куммера. Она разлагается в степенной ряд, сходящийся при всех rij.
называется функцией Куммера. Она разлагается в степенной ряд, сходящийся при всех rij.
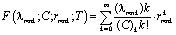 , (16)
, (16)
Функция G(αmnk;c;rmnk) через 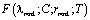 выражается следующим образом:
выражается следующим образом:
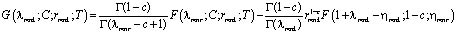 ,
,
где Г – гамма функция.
После определения давления в поровой жидкости осадку уплотняемого слоя грунта можно вычислить по формуле:
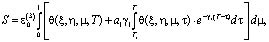 (17)
(17)
где
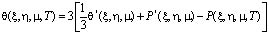 , (18)
, (18)
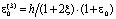 .
.
Выражения Р0 и P, входящие в последнюю зависимость, находятся из (6) и (12). Подставив их в (18) и (17) осадку слоя грунта представим в виде:
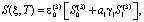 (19)
(19)
где
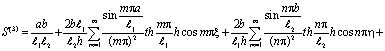
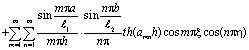 , (20)
, (20)
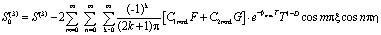 ,
,
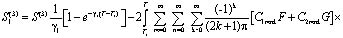
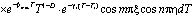 . (21)
. (21)
Таким образом, пространственная задача консолидации многофазного грунта с учетом его линейной ползучести и старения скелета, можно сказать, решена полностью. Выражения (12) и (19) при (20), (21) дают возможность установить закон изменения порового давления и осадку уплотняемого массива во времени и пространственных координатах. Причем? в эти решения, полученные в замкнутом виде, входят различные параметры грунта.
Анализ полученных решений на основе численных расчетов показал, что учет старения скелета приводит качественно к новым результатам теории уплотнения.
Следует заметить, что на основе выражений (6) – (21) можно получить решения задач и для других случаев нагружения грунтового основания. В частности давление в поровой жидкости (6) и (12) от сосредоточенной силы соответственно выглядит так:
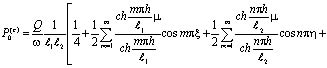
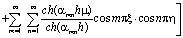 , (22)
, (22)
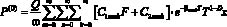
 . (23)
. (23)
Выражения (20), (21) для данного случая при (22) и (23) имеют вид:
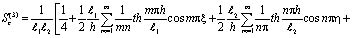
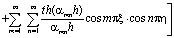 , (24)
, (24)
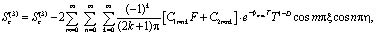
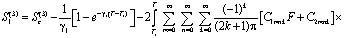
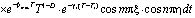 . (25)
. (25)
Анализ численных результатов показал, что продолжительность процесса уплотнения глинистого грунта почти не зависит от скорости фильтрации. Этот фактор видимо объясняется тем, что если проницаемость грунта очень велика, то процесс уплотнения в основном определяется его вязким сопротивлением. С другой стороны, если водопроницаемость грунта мала, то уменьшение объема грунта может произойти, лишь при условии отжатия воды из его пор. В то же время уменьшение объема грунта ведет к сжатию газообразной фазы и появлению порового давления. Возникновение порового давления влечет за собой фильтрацию воды через грунт.
Следовательно, если уменьшение объема грунтового массива больше по величине объема выжимаемой из его пор воды, то, по-видимому, происходит увеличение порового давления и увеличение фильтрационного расхода. Но в какой-то момент времени между ними наступает равновесие, тогда увеличение порового давления прекращается и после него начинается его уменьшение. При этом грунт малой плотности под действием внешней нагрузки способен в короткое время претерпеть большую осадку, что влечет за собой большое сжатие воздуха и как следствие этого, поровое давление принимает большое значение. Однако при увеличении плотности грунта деформация уплотняемого слоя значительно меньше, так как она осуществляется за счет более прочных слоев связанной воды. В этом случае газообразная составляющая сожмется меньше, чем при меньшей плотности грунта, следовательно, поровое давление в нем будет ниже.
Таким образом, процесс возникновения и возрастания порового давления является сложным процессом, зависящим не только от величины, приложенной внешней нагрузкой, но и от времени, плотности и водонасыщенности грунта. Причем, чем плотнее грунт и вязок, тем больше период времени, необходимый для достижения его стационарного напряженного состояния.



