Известны конструкции дисковых гидравлических машин, которые могут использоваться как в качестве насосов, так и в качестве турбин [7, 8].
Теоретические исследования динамики дисковых гидромашин в основном касаются решению задач о течении жидкости в кольцевой щели между вращающимися дисками насосов [9]. Эти решения базируются на уравнениях Новье-Стокса с различными краевыми условиями. Следует отметить, что исследования дисковых насосов показали их преимущества в определенных областях применения перед лопастными по эффективности, а также по шумовым и кавитационным характеристикам [1]. Эти преимущества относятся также и к дисковым турбинам. Однако до настоящего времени нет теоретических разработок для расчета силовых характеристик дисковых турбин в зависимости от параметров водосброса и геометрии конструкции.
Цель исследования. Целью исследования является получение аналитических зависимостей для определения крутящего момента и мощности на валу дисковой турбины от сил вязкого трения и сил Кориолиса в зависимости от геометрических параметров и расхода жидкости.
Материалы и методы исследования
Для анализа силового взаимодействия жидкости с рабочими органами дисковой турбины рассмотрим схему взаимодействия потока воды с дисками ротора турбины, которая в упрощенном виде изображена на рис. 1.
Особенность дисковой гидротурбины заключается в том, что её ротор 1 состоит из набора плоских дисков 2 толщиной d радиусом R в n количестве соединенных в пакет, жестко установленный на валу отбора мощности, который смонтирован на подшипниковых опорах в корпусе 3 с конфузором 4. Вода из диффузора 4 под напором Н и с расходом Q подается через щелевое отверстие 5 шириной с и высотой h, попадая в зазоры между дисками величиной b, раскручивает ротор турбины за счет сил вязкого трения. В отличие от традиционных турбин, в которых вращение ротора турбины обеспечивается за счет сил реакции потока воды, воздействующего на лопасти турбины как на преграду. Вода, передавшая кинетическую энергию ротору турбины, выводится через центральное отверстие радиусом r по направлению оси Z.
Рассмотрим силовое взаимодействие напорного потока жидкости с дисками ротора турбины в цилиндрической системе координат (Z, ρ, φ). Будем считать, что турбина имеет одну степень свободы и может вращаться только вокруг оси Z. Примем уплотнения идеальными, и не будем принимать во внимание взаимодействие жидкости с конструктивными элементами крепления дисков на валу отбора мощности ротора турбины.
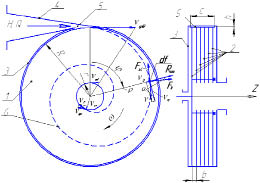
Рис. 1. Схема дисковой турбины
Результаты исследования и их обсуждение
Результаты исследования и их обсуждение. Основными движущими силами, обеспечивающими движение роторов турбины, будут силы вязкого трения (сцепления) между поверхностью дисков и жидкостью. Элементарную силу вязкого трения для единичного элемента по известным зависимостям можно записать в виде [4, 5]
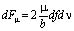, (1)
где μ – коэффициент вязкого трения, зависящий от вязкости жидкости, температуры, материала и шероховатости поверхности дисков, величины давления и, очевидно, он может быть определен только экспериментальным путем; df – площадь элемента (так как элемент жидкости взаимодействует в зазоре одновременно с двумя дисками, то принят коэффициент 2); dv – абсолютная скорость элемента жидкости.
Элементарная сила вязкого трения будет создавать крутящий момент на роторе турбины относительно оси вращения Z
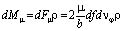, (2)
где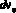 
– тангенциальная составляющая скорости элемента жидкости.
Для определения суммарного крутящего момента необходимо знать краевые значения скорости жидкости на входе в зазоры между дисками и на выходе из них. С учетом расхода жидкости на входе в зазоры между дисками значение тангенциальной скорости можно записать в следующем виде
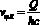, (3)
Принимая угловую скорость дисков постоянной для определенного расхода жидкости и сил сопротивлений, с учетом пропорционального изменения линейной тангенциальной скорости в зависимости от радиуса приложения её значение можно вычислить по формуле
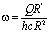, (4)
здесь R′ – приведенный радиус, физический смысл которого заключается в следующем. Если турбина работает в холостом режиме, то скорость вращения ротора будет максимальная, а мощность турбины минимальная, то есть энергия потока жидкости будет затрачиваться, лишь на преодоление трения в подшипниках. В таком режиме относительная тангенциальная скорость потока и дисков почти нулевая. При подключении нагрузки скорость вращения ротора турбины падает.
Из выражения (4) видно, что на холостом режиме работы турбины, когда приведенный радиус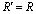 
, угловая скорость вращения максимальна. В реальности при холостом режиме преодолеваются сопротивления в подшипниках и уплотнениях. При этом приведенный радиус несколько меньше наружного радиуса дисков. При подключении полезной нагрузки приведенный радиус уменьшается и, соответственно снижается угловая скорость вращения ротора турбины.
Выражение для тангенциальной скорости жидкости на выходе из зоны взаимодействия с дисками ротора турбины можно записать в виде
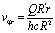. (5)
С учетом краевых условий и допущений напорный поток жидкости будет разгонять ротор турбины наприведенном радиусе R′ и в первом приближении можно записать уравнение (2) в интегральной форме в следующем виде
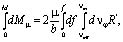(6)
где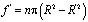 
– суммарная площадь взаимодействия, на которой создается крутящий момент от сил вязкого трения.
Учитывая зависимости (3) и (5), проинтегрировав выражение (6), принимая во внимание, что движение ротора турбины происходит за счет сил противодействия силам вязкого трения, получим окончательно выражение для крутящего момента на роторе турбины от сил вязкого трения
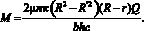(7)
Здесь следует отметить, что при холостом ходе турбины, когда отсутствуют силы полезного сопротивления, приведенный радиус R′ будет близок к наружному радиусу дисков R ротора турбины. В этом случае крутящий момент на турбине минимален, а угловая скорость вращения максимальна. При нагруженной турбине угловая скорость вращения турбины падает и, соответственно уменьшается приведенный радиус R′, а крутящий момент на турбине при этом возростает.
Из уравнения (7), принимая крутящий момент на валу турбины равным суммарному крутящему моменту сил трения и полезной нагрузки определяется приведенный радиус R′ по следующей зависимости
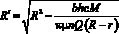. (8)
Мощность на валу ротора дисковой турбины с учетом (4) и (7) определится по следующей зависимости
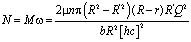. (9)
Для анализа полученных аналитических зависимостей необходимо экспериментальное определение коэффициента вязкого трения μ. Для этих целей была разработана методика и изготовлен специальный стенд.
Стенд состоит из рамы, на которой установлен электродвигатель с блоком из 7 звездочек разного диаметра и два кронштейна с направляющими блоками для приводной цепи. Пакет из нескольких пластин или пластина определенного размера, которые погружались в емкость с водой и закреплялись при помощи тонкой нити к динамометру, который соединялся с цепью такой же нитью.
Для определения коэффициента вязкого трения был изготовлен пакет из пяти пластин размером 0,1х0,15 м из того же материала, что диски турбины, а именно из алюминия толщиной 1,2 мм. Зазор между пластинами b= 0,0018 м определялся толщиной шайб.
Методика определения коэффициентов заключается в следующем.
Пакет из пластин или пластина погружались в воду. Затем кронштейны с блоками устанавливались в плоскости одной из семи звездочек, на которую устанавливалась цепь. Для замера силы трения Fμ в экспериментах использовался динамометр. Скорость определялась в соответствии с радиусом R задействованной в испытании звездочки и частоты n = 1380 об/мин вращения вала электродвигателя по формуле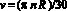 
.
Коэффициент вязкого трения определяется из зависимости (1) по формуле
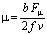, (10)
где f = 2·5·0,15·0,1=0,15 м2 – суммарная площадь пакета пластин; b =0,0018 м – зазор между пластинами; Fm – сила сопротивления, которая определяется экспериментально в зависимости от скорости v.
Экспериментальные значения коэффициента вязкого трения μ в зависимости от изменения скорости ν потока воды, аппроксимированы линейной функцией с стандартным отклонением 0,00013925 и среднеквадратичной ошибкой 0,8493682 в виде уравнения
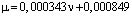. (11)
Следует отметить, что в зазорах между дисками турбины скорость элемента жидкости меняется от максимального на входе в зазоры до минимальной на выходе из них. В этой связи коэффициент вязкого трения также будет меняться в зависимости от значения скорости. Это обстоятельство сложно для аналитического выражения. В первом приближении можно принять коэффициент вязкого трения постоянным в зазорах, приняв скорость элемента жидкости как среднюю тангенциальную скорость. Эта скорость с учетом зависимости (4) запишется в виде
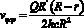. (12)
С учетом (11) и (12) выражение (9) запишется в следующем виде.
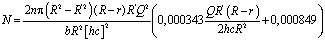. (13)
Очевидно, основными движущими силами, обеспечивающими движение роторов турбины, будут силы вязкого трения (сцепления) между поверхностью дисков и жидкостью. Однако, поскольку в зазорах между дисками турбины жидкость перемещается относительно дисков с некоторой относительной скоростью, то будут возникать Кориолисовы силы инерции. Тангенциальные составляющие этих сил будут создавать на валу турбины крутящий момент, который представляет следующею зависимость [4, 5]
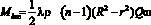. (14)
Мощность на валу дисковой турбины от сил Кориолиса определится с учетом (14) и (4) по следующей зависимости
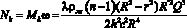. (15)
Для анализа полученных аналитических зависимостей (14) и (15) необходимо экспериментальное определение коэффициента трения λ жидкости с поверхностью смоченных дисков. Методика определения коэффициента трения λ аналогична описанной выше методики определения коэффициента вязкого трения. В эксперименте использовалась прямоугольная пластина размерами 0,2х0,15 м соответствующего дискам турбины материала, а именно из алюминия толщиной 1,2 мм.
Коэффициент трения по смоченной поверхности определялся по известной зависимости
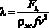, (16)
где f =2·0,2·0,15=0,06 м2 – суммарная площадь смоченной поверхности, rж= 1020 кг/м3 – плотность воды при температуре 20 °С, Fl – сила сопротивления, которая определялась экспериментально в зависимости от скорости v.
Экспериментальные значения пяти средних из десяти замеров сил трения F при разных скоростях ν позволили определить среднее значение коэффициента трения по смоченной поверхности λср = 0,0024.
Графики зависимостей мощности дисковой турбины создаваемой силами вязкого трения от расхода воды Q [м3/с], вычисленной по формуле (13) (сплошная линия) и от сил Кориолиса – по формуле (15) (пунктирная линия) для следующих параметров: R=0,2 м, r = 0,06 м, n=30, c=0.06 м, h=0,01 м, b =0,0018 м, λ = 0,0024 при R′ = 0,1 м – представлен на рис. 2.
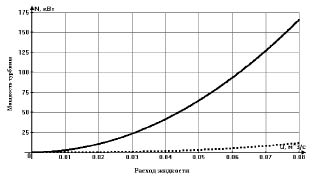
Рис. 2. График аналитической зависимости мощности N на роторе дисковой турбины создаваемой силами вязкого трения (сплошная линия) и силами Кориолиса (точечная линия) от расхода Q воды
Из графика (рис. 2) видно, что мощность на валу дисковой турбины, создаваемая силами Кориолиса значительно меньше, чем мощность от сил вязкого трения. С возрастанием расхода жидкости доля мощности от сил Кориолиса, по сравнению с мощностью от сил вязкого трения, растет и при расходе равном 0,08 м3/с составляет 7 %.
Полученные аналитические зависимости позволяют проводить анализ влияния параметров напорной жидкости, конструкции и геометрических размеров дисковой турбины на её динамические характеристики. Эти зависимости применимы для инженерных расчетов дисковых турбин.
Выводы
Полученные аналитические зависимости позволяют не только определить мощность дисковой гидротурбины, но и показывают пути их конструкторской модернизации. В частности разработана и запатентована новая конструкция дисковой турбины, позволяющая значительно увеличить эффективность работы за счет увеличения площади контакта жидкости в зазорах между дисками турбины. Однако, следует отметить, что корректное использования полученных зависимостей возможно после проведения более детальных экспериментальных исследований реальных турбин в производственных условиях и сопоставление их с аналитическими зависимостями. Эти исследования запланированы и проводятся работы по изготовлению опытного образца дисковой гидротурбины модернизированной конструкции.
Работа выполнена в рамках гранта Комитета науки Министерства образования и науки Республики Казахстан (номер госрегистрации 0113РК00415).