При автоматизированном проектировании элементов, узлов и устройств технологического оборудования разработчик зачастую встречается с проблемой малых выборок, т. е. отсутствия необходимого количества эмпирических данных для принятия рационального конструктивно-технологического решения [1]. Особо остро проблема малых выборок ощущается в те моменты, когда получение эмпирических данных сопровождается существенным увеличением стоимости проектных работ.
Для «обхода» проблемы малых выборок при оценивании плотностей вероятностей p(x) увеличим объем исходных данных 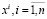 , за счет результатов статического моделирования. С этой целью в β-окрестности каждой i-й точки выборки осуществим m имитаций с законом распределения p2(x). Полученная статическая выборка
, за счет результатов статического моделирования. С этой целью в β-окрестности каждой i-й точки выборки осуществим m имитаций с законом распределения p2(x). Полученная статическая выборка 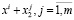 ,
, 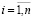 , при равновероятных значениях
, при равновероятных значениях 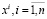 , соответствует смеси плотностей вероятностей:
, соответствует смеси плотностей вероятностей:
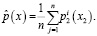 (1)
(1)
Нетрудно заметить, что непараметрическая оценка (1) имеет вид
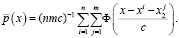 (2)
(2)
Существующий парадокс традиционных методов идентификации стохастических моделей состоит в сопоставлении конечной случайной выборки наблюдений переменных изучаемых объектов с конкретным набором параметров модели, оптимальном в некотором смысле. Предлагается принципиально новый рандомизированный подход определения коэффициентов размытости непараметрических решающих правил на основе процедуры их случайного выбора, который рассматривается на примере оптимизации алгоритмов формирования литографических процессов [2].
Формирование случайной последовательности коэффициентов размытости при оценивании плотности вероятности p(x) осуществляется на основе выборки расстояний между исходными наблюдениями (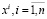 ) и их k – ближайшими соседями.
) и их k – ближайшими соседями.
Рандомизированный метод оптимизации рассмотрим на следующем примере. Пусть 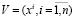 – выборка из n статистически независимых наблюдателей случайной величины
– выборка из n статистически независимых наблюдателей случайной величины 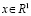 с плотностью вероятности p(x), вид которой неизвестен. Будем считать, что p(x) ограничена и непрерывна со всеми своими производными до второго порядка включительно. В качестве приближения по эмпирическим данным V искомой плотности вероятности p(x) примем статистику типа Розенблатта – Парзена [3]
с плотностью вероятности p(x), вид которой неизвестен. Будем считать, что p(x) ограничена и непрерывна со всеми своими производными до второго порядка включительно. В качестве приближения по эмпирическим данным V искомой плотности вероятности p(x) примем статистику типа Розенблатта – Парзена [3]
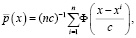 (3)
(3)
где 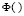 – ядерные функции, удовлетворяющие условиям положительности, симметричности и нормированности;
– ядерные функции, удовлетворяющие условиям положительности, симметричности и нормированности; 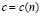 – последовательность положительных чисел (коэффициентов размытости) таких, что
– последовательность положительных чисел (коэффициентов размытости) таких, что
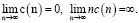 (4)
(4)
Свойства непараметрической оценки плотности вероятности (3), такие как асимптотическая несмещенность, состоятельность, сходимость почти наверное к p(x), подробно рассмотрены в работе [4].
Для сравнения традиционного и рандомизированного метода оптимизации непараметрической оценки плотности вероятности определим отношение 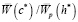 соответствующих им асимптотических выражений среднеквадратических критериев при оптимальных параметрах c и h.
соответствующих им асимптотических выражений среднеквадратических критериев при оптимальных параметрах c и h.
Из условия минимума 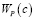 и
и 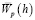 по c и h нетрудно получить
по c и h нетрудно получить
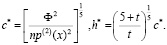 (5)
(5)
При оптимальных параметрах c*, h* отношение
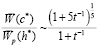 (6)
(6)
меньше единицы при конкретных значениях параметра t закона распределения p(c) коэффициентов размытия ядерных функций.
Однако использование непараметрической оценки со случайными значениями коэффициентов размытия ядерных функций
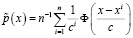 (7)
(7)
позволяет снизить смещение при оценивании плотности вероятностей по сравнению с традиционной статистикой типа (3).
Можно показать, что асимптотическое выражение смещения
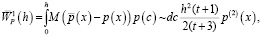 (8)
(8)
а его отношение к соответствующему смещению 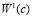 для традиционной непараметрической оценки при оптимальных параметрах c* и h*
для традиционной непараметрической оценки при оптимальных параметрах c* и h*
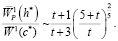 (9)
(9)
Если параметр t плотности вероятности 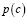 больше или равен 2, то отношение (9) меньше единицы.
больше или равен 2, то отношение (9) меньше единицы.
Анализ выражений (5), (8) показывает, что непараметрическая оценка плотности вероятности со случайными значениями коэффициентов размытости (7) обладает свойствами асимптотической несмещенности и состоятельности. Она характеризуется пониженным смещением (9) и несколько большим значением среднеквадратического отклонения (6) по сравнению с непараметрической статистикой (3). Следует ожидать проявления потенциальной эффективности непараметрической оценки плотности вероятности (7) при конечных объемах статистических данных.
Реализация «обхода» проблем малых выборок при оценивании плотностей вероятностей p(x) обеспечивается не только увеличением объема исходных данных 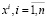 , но и результатами технического моделирования, т.к. сложность и многообразие процессов функционирования проектируемых технических систем не всегда позволяют получать для них адекватные математические модели, сформулированные в виде различных аналитических соотношений.
, но и результатами технического моделирования, т.к. сложность и многообразие процессов функционирования проектируемых технических систем не всегда позволяют получать для них адекватные математические модели, сформулированные в виде различных аналитических соотношений.
Возникает необходимость изменений структуры системы управления для повышения ее эффективности. Нужно определить контрольные точки – моменты в реализации проекта, в которых будет проводиться анализ эффективности структуры [5].
Можно выделить следующие принципы выбора опорных точек:
- завершение важнейших этапов реализации проекта;
- события передачи существенных результатов в другие подсистемы;
- события, не управляемые в рамках данного комплекса операций.
Введем некоторые обозначения и формализуем наиболее важные ограничения на выбор очередной контрольной точки. Пусть tg – g-я контрольная точка, 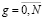 , где
, где 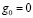 – начало реализации проекта,
– начало реализации проекта, 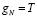 – срок его завершения. Существует некоторое минимальное D, на величину которого может отстоять контрольная точка от предыдущей. Если эта величина меньше D, то такая точка неэффективна, так как нельзя принять решение в столь короткий срок. Таким образом, имеет место ограничение:
– срок его завершения. Существует некоторое минимальное D, на величину которого может отстоять контрольная точка от предыдущей. Если эта величина меньше D, то такая точка неэффективна, так как нельзя принять решение в столь короткий срок. Таким образом, имеет место ограничение:
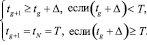 (10)
(10)
Если обозначить 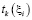 как плановые сроки завершения i-й работы, то
как плановые сроки завершения i-й работы, то
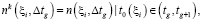 (11)
(11)
где 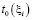 – плановое начало работы,
– плановое начало работы, 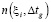 – количество работ, выполняемых в период
– количество работ, выполняемых в период 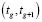 , а
, а 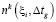 – количество работ, которые завершат свое выполнение в этот период.
– количество работ, которые завершат свое выполнение в этот период.
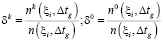 (12)
(12)
Показатели (12) можно использовать для приближенного определения степени изменения состава выполняемых работ. Если эти изменения велики, то, возможно, надо изменить и структуру системы. Если же значения этих показателей малы, то структура системы не нуждается в оптимизации [5].
Пусть величины αj и βj показывают потери, которые несет система при простое или перегрузке j-го узла. Зная эти величины, можно выразить ограничение на допустимые затраты от неоптимальной структуры:
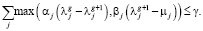 (13)
(13)
Это ограничение определяет границы допустимой неоптимальности системы управления, где γ обозначает суммарные оценочные затраты на проведение процедур анализа и оптимизации организационной структуры.
Кроме того, на неэффективность структуры системы управления указывает также увеличение числа внешних и внутренних связей в каждом комплексе операций. Необходимо также установить для каждой связи веса λpg, характеризующие их интенсивность.
Задачу оптимизации выбора контрольных точек можно записать так:
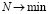 (14)
(14)
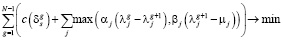 (15)
(15)
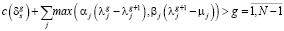 (16)
(16)
Таким образом, имеем модель оптимизации выбора контрольных точек (с учетом ограничений, принятых выше). Минимизируется количество точек, чтобы управление стало наиболее дешевым, а также минимизируются потери от неоптимальности структуры управления.
Далее рассматривается оптимизация графика работ и распределения ресурсов при управлении интенсивностями отдельных операций.
Рассмотрим методику решения двух типов задач: управление интенсивностью работ с минимизацией затрат и управление объемом работ при ограничениях на имеющиеся ресурсы [5].
На практике чаще всего имеет место дискретная зависимость скорости выполнения операции от затрат, которую можно представить следующим образом:
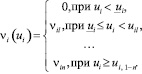 (17)
(17)
Будем считать, что скорость выполнения операции не изменяется непрерывно. Интенсивность 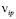 является функцией от интенсивности затрат uip, следовательно величина интервала tip, за который i-я работа выполнится также является функцией от
является функцией от интенсивности затрат uip, следовательно величина интервала tip, за который i-я работа выполнится также является функцией от 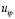 .
.
Каждой работе поставим в соответствие величины 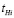 и
и 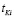 , которые определяют начало и конец выполнения i-й работы. Если элементарные подработы рассматривать как отдельные работы сетевого графа, то можно представить модель в виде:
, которые определяют начало и конец выполнения i-й работы. Если элементарные подработы рассматривать как отдельные работы сетевого графа, то можно представить модель в виде:
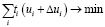
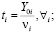
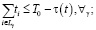 (18)
(18)
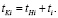
Решение этой задачи является очень сложным, поэтому необходимо ее линеаризовать. Это достаточно легко сделать, если функции зависимости скорости выполнения операции от затрат <<boll55.wmf>> принять в предложенном выше виде. Тогда для каждой выполняемой i-й работы можно установить возможные варианты ее выполнения.
Важной проблемой также является распределение функций между проектной и организационной системами управления, из-за чего часть функций по управлению (например, определение сроков реализации, распределение ресурсов) остаются прерогативой центра, что не всегда эффективно.
Данный тип структуры целесообразно применять в крупных проектах, условия реализации которых не полностью определены. Таким образом, в чистом виде ни одна из существующих структур не является идеальной.
Пусть определен общий объем работ по проекту, на основании которого руководитель проекта разрабатывает график работ. В общем виде такой график может быть представлен в виде системы, состоящей из объектов трех видов.
Будем использовать теоретико-графовое описание системы:
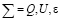 ,
,
где Q – множество вершин, U – множество ребер, 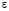 – отношение инцидентности, которое каждому ребру из U ставит в соответствие пару вершин из Q [5]:
– отношение инцидентности, которое каждому ребру из U ставит в соответствие пару вершин из Q [5]:
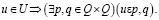 (19)
(19)
Функции описывают поведение элементов системы и представляются набором множеств: 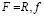 , где
, где 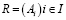 – семейство некоторых базовых множеств Ai (сигналов, траекторий, ресурсов, т. е. множеств, на которых задаются функции); f – множество всех отображений
– семейство некоторых базовых множеств Ai (сигналов, траекторий, ресурсов, т. е. множеств, на которых задаются функции); f – множество всех отображений
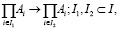 (20)
(20)
то есть, функций, отражающих определенные задачи реализации проекта. Это связано с затратой ресурсов (денежных средств, сырья и т. д.). В этом случае необходимо учитывать связи, обусловленные наличием ограничений типа
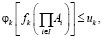 (21)
(21)
где uk – лимит ресурсов, выделенный для реализации k-й функции, ϕk – потребление ресурсов для реализации функции fk.
Таким образом, график работ – это структура, вершинам которой поставлены в соответствие функции, а ребрам – базисные множества, на которых эти множества определены. Каждая вершина характеризуется объемом потребляемых ресурсов, временем выполнения своих функций, а каждое ребро может характеризоваться, например, пропускной способностью [5].
Для построения эффективной системы управления необходимо оптимизировать распределение функций f по узлам системы Q. Введем булевы переменные
 (22)
(22)
В качестве целевой функции модели распределения функций по узлам можно взять один из следующих функционалов [5]:
минимизация суммарных затрат на выполнение задач
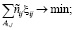 (23)
(23)
минимизация суммарного времени выполнения задач
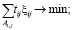 (24)
(24)
минимизация максимального времени решения задач
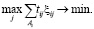 (25)
(25)
В зависимости от особенностей системы управления проектами, целочисленная оптимизационная модель распределения отдельных задач проекта по узлам компонуется из приведенных целевых функций и ограничений.
Заключение
Для повышения эффективности проектирования систем используют модели, сформулированные выше: управления интенсивностью выполнения отдельных работ с минимизацией затрат на интенсификацию, управления объемом выполненных работ при ограничениях на имеющиеся ресурсы. При некоторой модификации данные модели сводятся к типовым задачам, решаемым с использованием стандартных методов исследования операций применяемых для решения линейных моделей.
Рассматриваемая модель является оптимизационной задачей целочисленного программирования и позволяет объединить структурные элементы проекта в группы, оптимальные с точки минимизации межгрупповых связей. В итоге объединяются два нижних уровня иерархической системы управления, во главе каждого из которых стоит система, управляющая функционированием данного комплекса.
В целом, анализ проблем формирования и реализации последовательности проектов показал, что программа их формирования требует некого механизма реализации этой программы, что предполагает определение исполнителей и распределение ограниченных ресурсов между ними. Отсюда возникает одна из основных задач – определение оптимальной очередности реализации проектов, включенных в программу, с целью получения максимального эффекта от вложенных средств.



