Уникальной особенностью механизма Посселье-Липкина, называемого инверсором, является возможность воспроизведения одной из его точек абсолютно прямолинейного движения. В приведённом на рисунке 1 инверсоре PBCDAP1 именно точка C движется теоретически строго по вертикальной прямой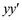 
.
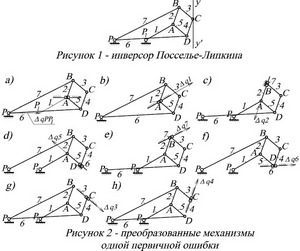
Однако такое точное движение возможно лишь при абсолютно точном выполнении всех звеньев механизма по длине, т.е. при условии PB=PD, AB=BC=CD=DA.
На практике обеспечить это условие невозможно, а потому возникает задача о нахождении истинного движения точки C. Обратимся к этой задаче с использованием теории точности механизма по Н.Г.Бруевичу [2].
Оценим, на сколько точно механизм на практике будет осуществлять предписанный закон движения. Первичными ошибками инверсора являются: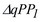 
- ошибка в расстоянии между стойками P и P1, и 
, 
, 
, 
, 
, 
, 
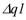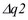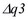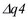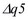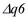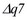- ошибки в длинах соответствующих звеньях.
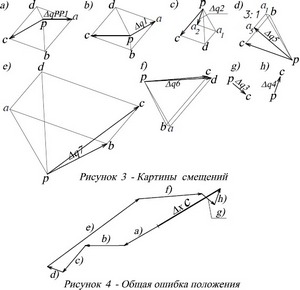
Задавая последовательно принятые ошибки, как возможные относительные смещения между звеньями, можно простроить восемь схем преобразованных (рис.2) механизмов по числу заданных ошибок, и по ним, методом планов смещений, найти ошибки смещения выходной точки C инверсора. Картины смещений показаны на рисунке 3. На них смещение точки C представляется вектором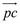 
в соответствующем масштабе.
Геометрическое сложение первичных ошибок позволяет найти общую ошибку заданного положения центра шарнира C. Именно на такую величину 
отклонится истинное положение точки С от прямой линии. Нахождение всех возможных отклонений положения точки C в N положениях механизма может быть истинным законом движения шарнира C.
Научный руководитель: Дворников Л.Т., д.т.н., профессор