Первая паровая машина в виде так называемого полного параллелограмма Уатта, была запатентована им в 1784г.[1]. Кинематическая схема параллелограмма приведена на рисунке1.
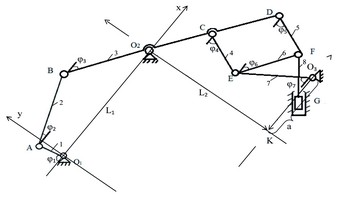
Рисунок 1- Кинематическая схема параллелограмма Уатта
При подаче пара в цилиндр G поршень начинает двигаться возвратно-поступательно и через шток передает движение в точке F звеньям 5,6, которые через систему звеньев 7,4,3,2 и 1 приводит к непрерывно-вращательному движению кривошипа1 ( АО1). Чтобы изучить, по какой траектории в действительности движется точка F,оторвем её от поршня 8 и проведем аналитическое исследование этого механизма.
Зададимся исходными параметрами: длинами звеньев - l1, l2, l3, l4, l5, l6, l7, l8 и заданным углом поворота – φ1-кривошипа, α0 – угол поворота декартовой системы координат. Свяжем механизм с неподвижной системой координат ХО1У, её выбираем таким образом, что начало координат совпадает с неподвижным шарниром О1. Обозначим углы поворота звеньев механизма как φ2, φ3, φ4, φ5, φ6, φ7 для проектирования на оси Х и У. Всего их получилось 6 неизвестных углов, следовательно нужно составить 3 векторных уравнения для нахождения неизвестных параметров. Представим замкнутый контур О1АВО2О1 ,из которого очевидным является векторное уравнение: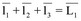 
. Проецируя это векторное уравнение на оси O1Х и О1У получаем
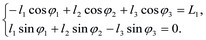(1)
Из этой системы могут быть найдены φ2 и φ3 в зависимости от φ1.
Составим векторное уравнение для второго замкнутого контура О2CEО3КО2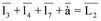 
. Проецируя это векторное уравнение на оси O1Х и О1У получим
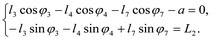(2)
откуда через найденный угол φ2 могут быть определены углы φ4, φ7.
Составим векторное уравнение для третьего замкнутого контура CDFEС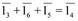 
. Проецируя это векторное уравнение на оси O1Х и О1У получаем
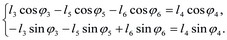(3)
Из этой системы могут быть найдены φ5 и φ6 в зависимости от φ3.
Общее решение приведенных систем уравнений позволяет найти закон движения точки F при условии исключения из механизма звена 8 – поршня со штоком.
Найдем сумму проекций звеньев через известные углы. Для этого составим систему уравнений проекций звеньев O2D, DF, FE, EO3 на оси Х и У системы координат
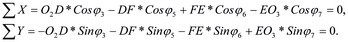
По известным значениям углов φ, полученным из (1), (2), (3) найдем уравнение движения точки F, по которому легко определить истинное движение этой точки.
Научный руководитель: Дворников Л.Т., д.т.н., профессор