Известна [3] трехподвижная кинематическая пара, обеспечивающая три относительных движения звеньев ВПП (рис. 1, а). В ней цилиндрическое тело круглого профиля движется в искривленной прорези, имея возможность воспроизводить при этом три относительных движения – вращаться относительно собственной геометрической оси, двигаться вдоль этой оси, и поступательно смещаться в прорези.
Описанная кинематическая пара может быть выполнена с цилиндрическим телом некруглого сечения, например эллиптическим. В этом случае окажется невозможным относительное вращательное движение цилиндра вокруг собственной оси и пара становится двухподвижной, с возможностью относительных поступательных движений во взаимно перпендикулярных направлениях (рис 1, б).
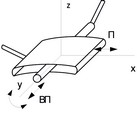 а)
а)
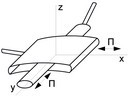 б)
б)
Отметим, что в практике машиностроения пока неизвестны случаи применения кинематических пар дозволяющих движение ПП. Еще Добровольским В.В. отмечалось: «Случай ПП не может быть реализован никакой конструкцией кинематической пары в собственном смысле этого слова» [2, c. 50].
Соединение звеньев, показанное на рисунке 1,б, решает эту задачу. Недостатком такого исполнения пары является неизбежное относительное зависимое движение звеньев вдоль оси Z. Покажем пример создания пространственного четырехзвенного механизма с использованием кинематической пары ПП. Такой кривошипно–ползунный механизм представлен на рисунке 2.
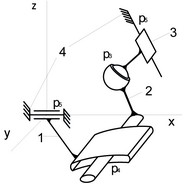
Рисунок 2 – Пространственный четырехзвенный кривошипно-ползунный механизм
Механизм состоит из неподвижного звена – стойки 4, относительно которой рассматривается движение, и трех подвижных звеньев: кривошипа 1, шатуна 2, и ползуна 3. Кривошип 1 образует со стойкой вращательную пару пятого класса (р5) – шарнир, шатун 2 входит с кривошипом в двухподвижную пару четвертого класса (р4), позволяющую совершать два относительных поступательных движения, а шатун 2 входит с ползуном 3 в сферическую трехподвижную пару третьего класса (р3). Ползун 3, в свою очередь входит со стойкой 4 в одноподвижную поступательную пару пятого класса.
Известно, что подвижность пространственных механизмов определяется формулой Малышева А.П. [1, стр.67, формула (2.8.)], имеющей вид
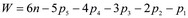 ,
,
где W – подвижность механизма, n – число подвижных звеньев, р5 р4 р3 р2 р1 – числа кинематических пар пятого, четвертого, третьего, второго и первого классов соответственно.
Описанный (рис. 2) механизм по приведенной формуле, при использовании n=3, р5=2, р4=1, и р3=1, дает подвижность W = 1. Т.е. вращательное движение кривошипа 1, беспрепятственно может передаваться на ползун 3 и обеспечивать его движение по заданному закону.
Научный руководитель: Дворников Л.Т., д.т.н., профессор



