Теоретический анализ напряженно-деформированного состояния плоских пластинок чаще всего опирается на решение уравнений в частных производных. Предлагаемый метод энергетического анализа краевых задач теории упругости основывается на составлении уравнений Лагранжа второго рода для упругих механических систем [1] и является одним из наиболее удобных способов упростить математические выкладки, сопровождающие применение волновой теории. Основу расчетов составляет приближенный метод, предложенный Дж. Рэлеем [2]. Точность предлагаемого метода целиком зависит от исходных предположений, задающих форму упругой поверхности исследуемой системы при ее равновесии. Один из методов подбора формы упругой поверхности можно сформулировать как принцип суперпозиции, при котором последовательно решаются задачи сопротивления материалов системы балок, на которые разбивается упругая система. Затем производится стыковка решений так, чтобы удовлетворить всем краевым условиям задачи.
Например, прямоугольную пластинку, защемленную с трех сторон и нагруженную равномерно распределенной нагрузкой, возможно представить как суперпозицию балок, параллельных оси х, защемленных с двух сторон, и консольных балок, параллельных оси у. После определения уравнений упругой оси U1(x) и U2(y) для балки, защемленной с двух сторон и для консольной балки форму упругой поверхности пластинки можно представить в виде произведения U(x,y)=α U1(x) U2(y), где α – коэффициент, подлежащий определению при решении задачи.
Возможен и иной подход, основанный на использовании уравнения краевого контура. Так, для равномерно нагруженной защемленной со всех сторон эллиптической пластинки с полуосями a и b, уравнение краевого контура представляет собой уравнение эллипса 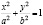 . Форму упругой поверхности пластинки в данном случае можно представить в виде:
. Форму упругой поверхности пластинки в данном случае можно представить в виде: 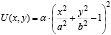 , очевидно удовлетворяющему условию защемления по краям.
, очевидно удовлетворяющему условию защемления по краям.
После подбора формы упругой поверхности решение задачи сводится к определению коэффициента α, постоянного при решении задач статики или переменного (зависящего от времени t) при решении задач динамики. Ниже приведены методы определения коэффициента α при решении статических и динамических задач теории упругости.
Для пластинок произвольной формы считаем форму их упругой поверхности заданной. Величину коэффициента α, входящего в выражение перемещений U(x,y) = α f(x,y), где f(x,y) – известная функция, будем искать из уравнения равновесия пластинки. При решении задач статики, как указывалось выше, α = const. Для определения α применим принцип возможных перемещений в обобщенных координатах [3], согласно которому обобщенные силы, соответствующие каждому возможному перемещению, равны нулю. Рассматривая действующие на пластинку силы как совокупность потенциальных сил упругой деформации и заданных непотенциальных сил, представим данное условие в виде: QП+QН = 0, где QП – обобщенная потенциальная сила, QН – обобщенная непотенциальная сила. Выражение для обобщенной потенциальной силы определяется из выражения потенциальной энергии П в виде частной производной. Обобщенная непотенциальная сила определяется как коэффициент перед вариацией обобщенной координаты в выражении суммы работ действующих на пластинку непотенциальных сил. Для получения выражения обобщенных сил по координате α выпишем выражение потенциальной энергии упругой деформации [4] в прямоугольных декартовых координатах: 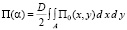 , где
, где 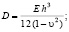
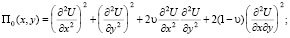
Е – модуль упругости, h – толщина пластинки, ν – коэффициент Пуассона; интеграл вычисляется по площади пластинки А. Тогда обобщенная потенциальная сила 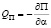 .
.
Обобщенная непотенциальная сила определяется по виду заданной нагрузки. Если, например, на пластинку действует сила F, приложенная в точке с координатами (х0,у0), то работа на выбранном перемещении может быть найдена из выражения 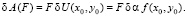 Таким образом, обобщенная непотенциальная сила, соответствующая сосредоточенной силе равна
Таким образом, обобщенная непотенциальная сила, соответствующая сосредоточенной силе равна 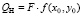 .
.
При распределенной по площади (a2–a1)×(b2–b1) нагрузке интенсивности q(x,y) возможную работу можно определить в виде интеграла
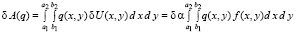
Следовательно, обобщенная непотенциальная сила, соответствующая распределенной по площади пластинки нагрузке, равна 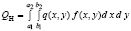 .
.
Наконец, если на пластинку действует пара сил с моментом 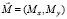 в точке (х0,у0), то элементарная работа равна
в точке (х0,у0), то элементарная работа равна
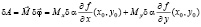 .
.
Отсюда следует, что обобщенная непотенциальная сила в этом случае может быть найдена в виде
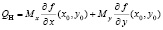 .
.
Для описания движения упругих систем с несколькими степенями свободы применяются, как правило, уравнения Лагранжа второго рода [3].
Покажем, как можно применить эти уравнения для описания движения упругой пластинки с одной степенью свободы на примере ее поперечных колебаний. Для этого представим поперечные перемещения точек пластинки с координатами (х,у) в виде: 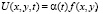 где α(t) – обобщенная координата, зависящая от времени. Уравнение Лагранжа с выбранной одной обобщенной координатой выглядит следующим образом:
где α(t) – обобщенная координата, зависящая от времени. Уравнение Лагранжа с выбранной одной обобщенной координатой выглядит следующим образом: 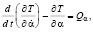 где T – кинетическая энергия пластинки,
где T – кинетическая энергия пластинки, 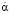 – обобщенная скорость (производная по времени от обобщенной координаты α), Qα – обобщенная сила, соответствующая выбранной обобщенной координате и включающая потенциальные и непотенциальные силы.
– обобщенная скорость (производная по времени от обобщенной координаты α), Qα – обобщенная сила, соответствующая выбранной обобщенной координате и включающая потенциальные и непотенциальные силы.
Поскольку упругая пластинка представляет собой систему с распределенной массой, выражение кинетической энергии найдем как интеграл
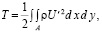
где ρ – плотность материала пластинки (масса единицы площади).
Для примера анализа вынужденных колебаний показано получение дифференциального уравнения, описывающего движение поверхности пластинки под действием сосредоточенной силы, приложенной посередине свободной границы пластинки. Полученные результаты легко распространить на любое расположения вибрационного аппарата, так как подробная методика, изложенная при решении поставленной задачи, позволяет легко сменить координаты точки приложения сосредоточенной силы.
Форму упругой поверхности стенки рудничной вагонетки выбираем из условия защемления прямоугольной пластинки с трех сторон (рисунок, а), раскладывая ее методом суперпозиции двух задач сопротивления материалов: одна – для балки, защемленной по концам (рисунок, б), вторая – для консольной балки (рисунок, в).
Уравнение упругой оси консольной балки длины b под действием сосредоточенной силы F можно представить в виде [4]:
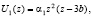 (1)
(1)
где 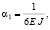 Е – модуль упругости, J – момент инерции балки.
Е – модуль упругости, J – момент инерции балки.
Расчет деформаций балки, защемленной по концам (рисунок, б) затруднен статической неопределимостью задачи. Пренебрегая продольными деформациями балки, установим, что степень статической неопределимости задачи равна двум. Для того, чтобы снять статическую неопределимость, воспользуемся методом сил [4], для чего составим систему алгебраических уравнений из условий равенства нулю деформаций на правой опоре основной системы (консольной балки):
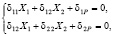 (2)
(2)
где δ11, δ12, δ22 – деформации балки, вызванные единичными силами Х1 = 1 и Х2 = 1, приложенными к правому концу вспомогательной системы, δ1Р, δ2Р – деформации от действия заданной силы F в точках приложения единичных сил. Для определения коэффициентов уравнения (2) получены аналитические выражения для изгибающих моментов, соответствующих рассматриваемым нагрузкам. После этого найдены значения деформаций δij по правилу Верещагина [4]. В результате получено:
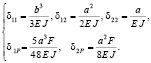 (3)
(3)
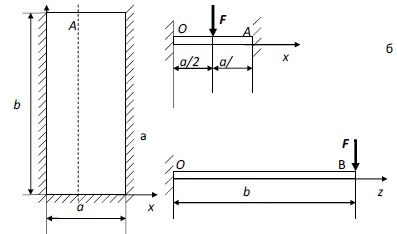
Расчетные схемы для прямоугольной пластинки: а - прямоугольная пластинка, защемленная с трех сторон; б - балка, защемленная с двух сторон; в - консольная балка
Подставляя полученные значения в уравнения (2) и сокращая на общий сомножитель, получаем систему алгебраических уравнений, определяющие «лишние» реакции:
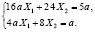 (4)
(4)
Таким образом, по величинам определенных реакций установим величину изгибающего момента в произвольном сечении данной защемленной по краям балки в виде:
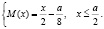 (5)
(5)
Далее проинтегрировано дифференциальное уравнение изогнутой оси балки:
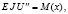 (6)
(6)
решение которого без учета постоянных сомножителей определяет форму изогнутой оси балки, защемленной по краям:
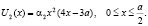 (7)
(7)
Перемножив выражения (1) и (7), установим, что изогнутая поверхность пластинки, защемленной с трех сторон, приближенно определяется уравнением:
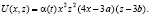 (8)
(8)
Кинетическую энергию стенки с учетом ее симметрии относительно вертикальной оси найдем как удвоенный интеграл, взятый по половине площади пластинки
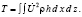 (9)
(9)
После интегрирования и подстановки пределов получим
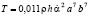 , (10)
, (10)
где α(t) играет роль обобщенной координаты и подлежит определению. Применяемый подход позволяет описать движение стенки рудничной вагонетки с помощью уравнения Лагранжа II рода [5]:
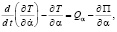 (11)
(11)
где П – потенциальная энергия пластинки, Qa – обобщенная непотенциальная сила, соответствующая выбранной обобщенной координате. Для ее определения нужно составить выражение элементарной работы на принятом возможном перемещении
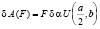 . (12)
. (12)
Следовательно,
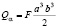 . (13)
. (13)
Выражение потенциальной энергии пластинки найдем в соответствии с [5] в виде:
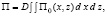 (14)
(14)
где 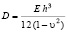 – цилиндрическая жесткость пластинки;
– цилиндрическая жесткость пластинки;
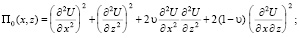
ν – коэффициент Пуассона.
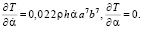 (15)
(15)
Далее находим подынтегральное выражение и величину потенциальной энергии (14):
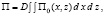 (16)
(16)
Откуда
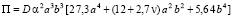 . (17)
. (17)
Подставив выражения (10), (13) и (17) в уравнение Лагранжа второго рода (11), получим
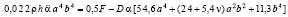 . (18)
. (18)
Таким образом, полученное уравнение имеет вид уравнения вынужденных колебаний [2]
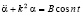 (19)
(19)
поэтому частота собственных колебаний стенки вагонетки равна
 (20)
(20)
Если при этом вынуждающая сила меняется по закону косинуса F = F0 cos n t, то коэффициент B, входящий в уравнение (19), определяется по формуле
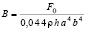 . (21)
. (21)
Решение дифференциального уравнения (21) позволяет, прежде всего, произвести выбор режимных пврвметров вибрационного устройства. В частности, если используется резонансный способ очистки, то математическое ожидание величины частоты вибратора должно примерно равняться частоте собственных колебаний рудничной вагонетки. Ниже в таблице приведены результаты расчетов частоты собственных колебаний некоторых видов рудничных вагонеток, вычисленных по формуле (20).
Результаты расчетов частоты собственных колебаний стенок рудничных вагонеток
|
Грузоподъемность, т |
Размеры вагонетки, м |
Частота колебаний, Гц |
|||
|
ширина |
длина |
высота |
торцевой стенки |
боковой стенки |
|
|
Вагонетки с глухим кузовом типа ВГ |
|||||
|
11,0 |
1,35 |
3,95 |
1,55 |
101,8 |
19,6 |
|
22,5 |
1,35 |
7,85 |
1,55 |
101,8 |
13,0 |
|
4,5 |
1,24 |
2,98 |
1,30 |
122,3 |
31,2 |
|
2,3 |
0,88 |
2,00 |
1,30 |
233,6 |
53,6 |
|
Угольные вагонетки |
|||||
|
3,3 |
1,32 |
3,45 |
1,30 |
109,1 |
26,7 |
|
2,5 |
1,24 |
2,80 |
1,30 |
122,3 |
33,5 |
|
1,6 |
0,85 |
2,70 |
1,20 |
251,2 |
37,3 |
|
1,4 |
0,85 |
2,40 |
1,23 |
250,7 |
42,4 |
Таким образом, настраивая вибрационный аппарат на определенную частоту, возможно добиться наилучшего эффекта. Следует иметь, однако, в виду, что приведенные в таблице результаты несколько завышены, так как расчеты проведены для чистой стенки (без налипшего материала).



