Важным свойством системы является способность при функционировании сохранять неизменными свои показатели в условиях случайных возмущений и взаимодействия с внешней средой. Это свойство внутренней саморегуляции систем определяется наличием совокупности обратных связей и сложных приспособительных реакций, направленных на устранение или максимальное ограничение факторов, нарушающих относительное устойчивое динамическое постоянство показателей внутренней среды. В биологических системах такое динамическое равновесное состояние называется гомеостазом.
Термин гомеостаз предложен в 1929 г. У. Кенноном, который считал, что физиологические процессы, поддерживающие стабильность в организме сложны и многообразны. Однако еще в 1878 г. К. Бернар указывал, что жизненные процессы направлены на поддержание постоянства условий жизни во внутренней среде. Аналогичные высказывания можно встретить в трудах Ш. Рише, И.П. Павлова, Э. Пфлюгера, Л.С. Штерна и др. Фактически гомеостаз имеет место при наличии устойчивых стационарных состояний, когда обеспечиваются условия саморегуляции и нормальное функционирование системы при изменяющейся внешней среды и случайных возмущений. Нарушение условий саморегуляции в области гомеостаза указывает на появление дефектов во внутренней структуре системы. Явление гомеостаза можно сравнить со свойством восстановления своих геометрических форм упругих тел, находящихся под воздействием механических сил. Появление остаточных явлений (не сохранения геометрических форм) в реакциях на механические воздействия указывает на нарушение внутренней структуры тел и их упругих свойств.
При моделировании представляет интерес изучение поведения системы, обладающей гомеостатическими свойствами за счет обменных энергоинформационных процессов. происходящих внутри системы и поддерживаемых поступлением энергии извне, когда сохраняется сбалансированное функционирование вблизи равновесного состояния. При малых колебаниях переменных состояния систему можно рассматривать как линейную, и ее поведение определяется характером равновесия. При больших колебаниях поведение системы не может быть описано линейными зависимостями, и оно носит достаточно сложный характер.
Функциональные возможности организма определяются его энергетическими ресурсами, восполняемые как за счет внутренних источников, так и поступлением из внешней среды. Наличие внутренних регуляторных механизмов и обратных связей обеспечивает сбалансированные динамические взаимодействия переменных состояния организма вблизи равновесных значений. Такое поведение организма характеризуется динамическим гомеостазом [1], и является одним из фундаментальных свойств, определяющих адаптационные возможности организма. На практике для оценки адаптационных возможностей организма применяют различные критерии [2, 3].
Нами для оценки гомеостатических свойств организма дополнительно вводится критерий динамической восприимчивости, когда формируются наблюдения, определяющие скорость отклонения переменных состояния организма от равновесных значений. При однократных измерениях, определение скорости является в общем случае некорректной задачей, которая в каждом конкретном случае может быть решена по-разному. Предложим для этих целей использовать среднегеометрические показатели.
Пусть силовая функция определяющая функционирование организма, определяется некоторой нелинейной зависимостью:
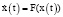, (1)
где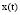 
– n-мерный вектор переменных состояния организма.
При нормальном функционировании организма можно выделить равновесные значения переменных состояния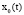 
и их допустимые отклонения 
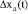. Метаболические процессы в пределах допустимых отклонений характеризуются некоторой энергией 
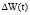, определяемой внутренними потенциальными возможностями, кинетическими ресурсами и активными затратами [4]. Для равновесных состояний выполняется равенство 
.
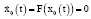При малых отклонениях компонент текущих траекторий от равновесных значений можно записать:
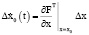
и
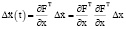. (2)
Уравнение (2) для устойчивых колебаний (обеспечивается при нормальном функционировании организма) является многомерным гармоническим осциллятором. Обобщенное решение для этого уравнения можно записать в виде:
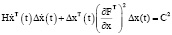, (3)
где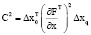 
– постоянная величина является энергетической характеристикой обменных процессов организма.
Можно ввести коэффициенты, отражающие относительное отклонение текущих значений переменных состояния и их скорости от допустимых значений
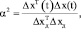
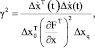
Здесь коэффициент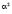 
характеризует возможные отклонения переменных состояния от взаимноравновестных значений 
; 
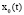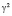– определяет относительную способность регуляторных механизмов организма обеспечивать условие устойчивого функционирования.
На практике контролировать эти коэффициенты удобно с помощью среднегеометрических показателей:
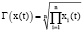
и
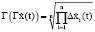
Относительное изменение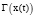 
и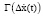 
во времени вблизи равновесных значений x0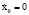 
;
.
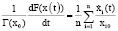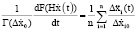С учетом (2) эти уравнения можно записать:
;
.
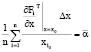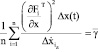Здесь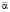 
характеризует среднее значение отклонения переменных состояния от 
, 
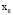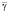определяет усредненное значение отклонений, динамической взаимосвязи переменных состояния организма, что фактически характеризует динамическую восприимчивость организма.
При практическом применении полученных выражений необходимо знать численные значения входящих в уравнения коэффициентов и их взаимную зависимость. Это можно сделать, используя обучающие выборки.
Программная реализация
Для выполнения поставленной задачи было разработано приложение в среде C++ Builder 2010. Исходные данные, нормы показателей и допустимые отклонения показателей от нормы считываются из файла.
Были рассчитаны показатели γ и α для оценки отклонения состояния здоровья пациентов от нормы. Получившиеся значения γ были усреднены по группам (группа здоровых пациентов и три группы больных по степеням тяжести). Результаты представлены в таблице.
Средние значения γ для групп пациентов
|
Группа |
Среднее значение γ |
|
Здоровые пациенты |
0,155 |
|
Больные пациенты с 1-й степенью тяжести |
0,809 |
|
Больные пациенты с 2-й степенью тяжести |
3,286 |
|
Больные пациенты с 3-й степенью тяжести |
4,491 |
Полученные значения показали, что для группы здоровых пациентов в среднем показатель γ незначительно отклоняется от 0, в то время как для групп больных пациентов он выше.
Заключение
Рассмотренные в статье алгоритмы и методы направлены на решение одной из важных проблем: создания эффективных инструментов решения задачи диагностики состояния здоровья людей.
Апробация программного обеспечения на реальных данных показала, что качество решения по вышеизложенному алгоритму удовлетворяет требованиям практического врача.
Работа выполнена в рамках проекта №1957 Гос. задания «НАУКА» Министерства образования и науки РФ.