Учебное пособие «Приложения кратных и криволинейных интегралов» разработано и подготовлено к изданию на кафедре «Высшая и прикладная математика» Уральского государственного университета путей сообщения (УрГУПС) доцентом кафедры, канд. пед. наук Гниломедовым П.И. Изданию присвоен номер ISBN 978-5-94614-316-5, материал пособия ориентирован на обучение студентов технических специальностей и направлений подготовки по математике в соответствии с ФГОС ВПО (рис. 1).
Рис. 1. Обложка издания
Содержание пособия распределено по двум главам: «Кратные интегралы», «Криволинейные интегралы». Отдельной главой представлены варианты заданий типового расчета.
Первая глава включает разделы: «Двойной интеграл и его вычисление» и «Тройной интеграл и его вычисление», содержащие основные теоретические сведения из соответствующих разделов курса высшей математики. После каждого раздела расположен параграф, в котором подробно рассматриваются геометрические приложения соответствующего интеграла. В конце главы отдельным разделом представлен параграф «Механические приложения кратных интегралов», также содержащий большое число примеров использования приемов кратного интегрирования и их использования в физических задачах по механике.
Аналогично структурирована и вторая глава, в которой содержатся разделы: «Криволинейный интеграл I рода», «Криволинейный интеграл II рода», соответствующие параграфы с примерами геометрических приложений интегралов. В конце главы также представлен параграф «Механические приложения криволинейных интегралов».
В разделе «Варианты заданий типового расчета» содержаться тридцать вариантов заданий, выполнение которых позволяет студентам успешно отрабатывать и закреплять изучаемый материал. Каждый вариант содержит восемь задач и имеет сквозную структуру, т.е. включает задачи по всем изученным разделам.
Отличительной особенностью данного пособия является богатый иллюстрируемый материал, поскольку практика показывает, что разделы интегрального исчисления, в том числе разделы, рассматривающие кратное интегрирование, интегрирование по дуге, вызывают значительные затруднения в понимании и, соответственно, в освоении как теоретических положений, так и практических приемов решения задач. Это связано, прежде всего, со значительными затруднениями формирования понятийного аппарата интегрального исчисления. Одной из причин является недостаточно прорабатываемые взаимосвязи между абстрактно-наглядным (чертеж, рисунок) и абстрактно-логическим (аналитическое выражение) образами представления основных понятийных объектов как теоретического материала, так и содержания математических задач [1].
В связи с этим, в пособии большое внимание уделено максимально наглядному сопровождению всех теоретических положений, основных типов задач, приемов кратного интегрирования и интегрирования по дуге на плоскости и в пространстве. Всего в пособии представлено сорок высококачественных рисунков в векторной графике, практически ко всем основным теоретическим положениям, типам задач и приемам интегрирования, рассматриваемых в пособии.
Приведем пример наглядного сопровождения теоретического материала из параграфа «Геометрическое приложение двойного интеграла» (рис. 2).
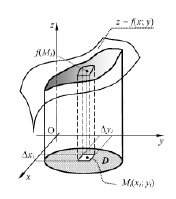
Рис. 2. Геометрический смысл двойного интеграла (объем тела)
Теоретическое обоснование использования двойного интеграла для определения объема тела, «продублированное» наглядным образом, позволяет сформировать аналитическое выражение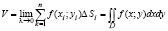 
.
В качестве примера органичного сочетания приемов интегрирования и их наглядного сопровождения приведем фрагменты решения задачи из параграфа «Геометрическое приложение криволинейного интеграла I рода» и сопровождающий рисунок (рис. 3)
Задача. Найти площадь части цилиндрической поверхности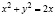 
, заключенной между плоскостью xOy и поверхностью сферы 
.
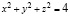Решение
Перейдем в полярную систему координат с помощью соотношений
.
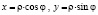Тогда уравнения для цилиндрической поверхности
,
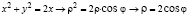для сферической поверхности
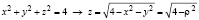
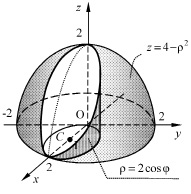
Рис. 3
… тогда площадь половины поверхности
.
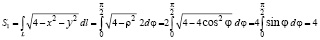Окончательно площадь всей цилиндрической поверхности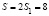 
.
Большое число подробно рассмотренных примеров решения задач и предложенный объем заданий для самостоятельного изучения, а также, задания типового расчета, дает возможность организовать как практические аудиторные занятия, так и самостоятельную работу студентов по освоению основных методов интегрирования, а уровень изложения теоретического материала позволяет использовать его в качестве лекционного.
Работа получила положительную рецензию канд. физ.-мат. наук, старшего научного сотрудника отдела прикладных проблем управления ИММ УрО РАН И.Н. Кандобы и канд. физ.-мат. наук, доцента кафедры «Высшая и прикладная математика» Уральского государственного университета путей сообщения (УрГУПС) П.П. Скачкова.
[1]Гурова Л.Л. Психология мышления. – М.: ПЕР СЭ, 2005. – 136 с. ISBN 5-9292-0134-Х