История открытия и последующее использование закона Тициуса-Боде весьма интересны, а дальнейшее исследование закона расположения планет и малых объектов Солнечной системы продолжаются вплоть до настоящего времени. Коротко приведем исторический анализ этой проблемы по источникам [1, 2].
В 1766 г. немецкий физик и математик Иоганн Тициус в своем переводе с французского книги Шарля Бонне «Созерцание природы» поместил примечание, в котором представил выведенную им формулу, определяющую расстояние планет от Солнца:
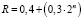. (1)
Здесь R – среднее расстояние планет от Солнца или большая полуось ее орбиты в астрономических единицах, n – показатель степени, равный – ∞; 0;1; 2; 3…..; соответственно для Меркурия, Венеры, Земли, Марса и т.д.
Сначала на полученную Тициусом зависимость мало кто из астрономов того времени обратил внимание. Она приобрела широкую известность, благодаря немецкому астроному Иоганну Боде (1747–1826 г.г.), который постоянно подчеркивал важность данной закономерности для Солнечной системы, излагая и комментируя ее в своих научных трудах. Именно по этой причине формула (1) стала называться законом или правилом Тициуса-Боде. Всеобщее признание она получила в 1781 г., когда была открыта планета Уран, среднее расстояние которой от Солнца (19,8 а.е.) примерно соответствовало расчетам по правилу Тициуса-Боде (19,6 а.е.). После открытия в последующем Нептуна (1846 г.) и Плутона (1930 г.), расстояния, которых от Солнца не укладывались в правило Тициуса-Боде, ему был нанесен сильнейший удар. Правило Тициуса-Боде перестало быть основой для дальнейших предсказаний [2]. В 1787 г. Вурм [2] нашел, что для известных тогда спутников Юпитера и Сатурна применимы соотношения вида: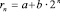 
. В 1913 г. Мэри Блэгг [2], анализируя логарифмы расстояний между планетами , пришла к выводу, что наилучший закон расстояний в планетной системе имеет вид геометрической прогрессии со знаменателем 1,7275, а не 2,0: 
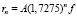[B + (α + nβ)], где А и В – положительные числа, а α и β – постоянные углы, f – функция с периодом 2π, принимающая значения от 0 до +1. Спустя 30 лет Ричардсон выполнил аналогичный анализ и пришел к аналогичному выводу:
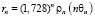, где ρn – функция периода 2π. В источниках полученные функции не приводятся в явном аналитическом виде, что затрудняет их использование.
Как справедливо отмечают многие исследователи, сегодня важен не поиск дальнейшего усовершенствования правила Тициуса-Боде, а важным является выяснение причин существования подобной закономерности, поскольку она, безусловно, связана с фундаментальными вопросами теории тяготения, происхождения и эволюции Солнечной системы. В этой связи отметим работу В.В. Шепелева [1]. Эта работа является лучшей с точки зрения обнаружения связи расположения планет и их спутников с радиусом центрального тяготеющего тела. Также с точки зрения наилучшего математического представления закона Тициуса-Боде являются работы Мэри Блэгг и Ричардсона Д.С. [2].
Цель работы
Объяснить физическую природу закономерности расположения планет в Солнечной системе. Тем самым внести вклад в решение проблем современной теории тяготения.
Решаемые задачи, направленные на достижение цели
Для достижения поставленной цели необходимо:
1. Проверить существование закономерности расположения планет в Солнечной системе, проверить выполнение этой закономерности для открытых в последнее время объектов в области за Нептуном, в так называемом поясе Койпера (от 30 а.е. до 55 а.е. от Солнца) и немного за этим поясом. Получить такую закономерность собственного вида.
2. Сопоставить ее с аналитическими результатами экспериментов дифракции света.
3. Сделать вывод о возможной дифракции гравитационных волн, излучаемых Солнцем.
Изложение содержания работы и интерпретация полученных результатов
Аналитическое исследование расположения планет в Солнечной системе. Экспериментальные данные использованы из источников[2, 3, 4]. Сначала была апробирована экспоненциальная зависимость вида:
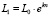(2)
где L1 – расстояние от планеты до Солнца, n – порядковый номер планеты – числа 1,2,3,.., е – основание натуральных логарифмов, L0 и k – коэффициенты. Расчет методом наименьших квадратов дал следующие значения коэффициентов: k = 0,543, L0 = 30 млн км. Результаты расчетов по уравнению (2) для планет и других объектов Солнечной системы соответственно приведены в табл. 1 и 2, а графическая анаморфоза представлена на рис. 1 в полулогарифмических координатах (линия 1). В таблицах приведены также относительные отклонения расстояния L1, рассчитанного по уравнению (2), от соответствующих фактических значений Lф, т.е. относительные погрешности:
.
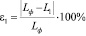При последующем анализе была использована зависимость расстояний планет в виде функции синуса, которая накладывается на экспоненциальную зависимость. На рис. 1 она представлена линией 2, а аналитически выражается уравнением:
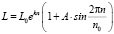. (3)
В этом уравнении L и n имеют тот же смысл, а коэффициенты L0 и k – те же значения, что и в уравнении (2); A и n0 – дополнительные коэффициенты. Расчет этих коэффициентов графоаналитическим методом при выполнении условия минимизации относительных погрешностей дал следующие результаты: А = 0,19, n0 = 6,3. По полученным значениям коэффициентов были рассчитаны расстояния L и относительные погрешности ε. Результаты приведены в таблицах (1) и (2). По данным таблиц видно, что уравнение (3) дает меньшие погрешности, чем уравнение (2). Также для объектов с большим удалением от Солнца (таблица 2) разброс расстояний Lф от L значительно больше, чем для планет (табл. 1). Это свидетельствует о том, что на периферии Солнечной системы (в поясе Койпера и далее) причина, по которой происходило формирование планет в Солнечной системе более слабая, чем вблизи Солнца.
Экспериментальное исследование дифракции света. Для исследования дифракции света, в частности, распределения интенсивности в дифракционной картине, определения длины световой волны, используют схему, приведенную на рис. 2. При этом экран (или датчики) располагают в положении 5. Для определения длины волны монохроматического света (например, от лазера) используют формулу:
dsin φ = m λ (4),
где d – постоянная решетки, φ– угол дифракции, m = 0,1,2,… – порядок дифракционного максимума, λ – длина волны. На рисунке максимумы показаны только в одну сторону.
Таблица 1
Характеристика планет (n = 1÷9) по уравнениям (2) и (3)
|
Наименование планеты |
n |
Lф, млн. км |
По уравнению (2) |
По уравнению (3) |
||
|
L1, млн. км |
ε1, % |
L, млн. км |
ε, % |
|||
|
Меркурий |
1 |
58 |
51,6 |
11,0 |
59,8 |
3,1 |
|
Венера |
2 |
108 |
88,9 |
17,7 |
104 |
3,7 |
|
Земля |
3 |
150 |
153 |
2,0 |
157 |
4,7 |
|
Марс |
4 |
228 |
263 |
15,3 |
226 |
0,9 |
|
Церера Паллада Юнона Веста |
5 |
414 415 399 353 |
453 |
|
368 |
|
|
Юпитер |
6 |
778 |
750 |
0,3 |
736 |
5,4 |
|
Сатурн |
7 |
1426 |
1342 |
5,9 |
1506 |
5,6 |
|
Уран |
8 |
2869 |
2310 |
19,5 |
2747 |
4,3 |
|
Нептун |
9 |
4496 |
3977 |
11,5 |
4303 |
4,3 |
|
Средняя относительная погрешность, % |
10,9 |
4,5 |
||||
Таблица 2
Характеристика занептуновых объектов (n = 10?14) по уравнениям (2) и (3)
|
Наименование объекта, его шифр и год открытия |
n |
Lф, млн. км |
По уравнению (2) |
По уравнению (3) |
||
|
L1, млн. км |
? 1, % |
L, млн. км |
?, % |
|||
|
Макемаке, FУ9, 2005 Орк, 2004 Хаумеа, EL61, 2003 Плутон,1930 Квавар, 2002 42301, UR163, 2001 48639, TL8, 1995 |
10 10 10 10 10 10 10 |
6850 5860 6413 5900 6493 7693 7858 |
6845 |
|
6172 |
|
|
(–), UR146, 2002 82075, YW143,2000 Объект OR10, 2007 Эрида, UB313,2003 |
11 11 11 11 |
7989 8697 10072 10157 |
11780 |
|
9543 |
|
|
26181, GQ21,1996 15874, TL66,1996 |
12 12 |
14154 15557 |
20276 |
|
18105 |
|
|
Объект RC105,2000 |
13 |
44500 |
34898 |
21,6 |
37472 |
15,8 |
|
Седна, VB12, 2000 |
14 |
78825 |
60066 |
23,8 |
71304 |
9,5 |
|
Средняя относительная погрешность, % |
23,7 |
13,5 |
||||
В наших исследованиях в схеме по рис. 2 мы экран поместили в положение 4, тогда картина дифракции видоизменилась, она приведена на рис. 3. Анализ данных дифракции света приведен в табл. 3. Используя данные L2ф табл. 3, полученные по рис. 3, были в полулогарифмических координатах построены зависимости 1 и 2, представленные на рис. 4. Даже при визуальном сравнении рис. 1 и 4 видно, что зависимости идентичные и должны описываться одинаковыми уравнениями. Действительно, для данных рис. 4 и табл. 3 уравнение в общем виде будет:
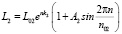, (5)
или с учетом значений коэффициентов:
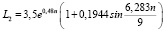, (6)
где n = 0,1,2,...; [L02] = мм. На основании совпадения уравнений 3 и 5 следует предположить, что расположение планет и других объектов Солнечной системы является следствием дифракции гравитационных волн.
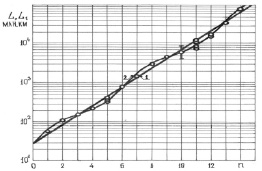
Рис. 1. Графическая анаморфоза зависимостей по уравнению (2) – линия 1 и уравнению (3) – линия 2
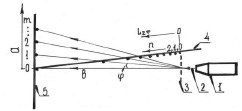
Рис. 2. Схема опыта по дифракции света. Обозначения: 1 – лазер; 2 – монохроматический луч света; 3 – дифракционная решетка; 4 – или 5 – экран, его расположение; L2ф – расстояние до дифракционного максимума при определенном n на экране 4; а – расстояние до максимума при определенном m на экране 5; в – расстояние от дифракционной решетки 3 до экрана 5
Рис. 3. Вид дифракционной картины по схеме рис. 2 ( положение экрана – 4)
Максимумы и минимумы дифракции гравитационных волн представляют собой сферические области, расположенные вокруг Солнца. Экспериментальная проверка гипотезы дифракции гравитационных волн с образованием минимумов и максимумов возможна путем замеров напряженностей гравитационного поля в областях расположения планет (и их спутниковых систем). Такие замеры нецеленаправленно проведены при полетах космических аппаратов «Пионер-10 и -11» [5] и расценены как «аномальные эффекты в Солнечной системе». Причем, максимумы напряженностей гравитационного поля согласно проведённым замерам приходятся на области расположения планет и их спутников.
Таблица 3
Анализ данных дифракции света по рис. 3.
|
Значение L2 по уравнению (5) в сравнении с его фактическим значением L2ф при определенном n. |
||||||||||
|
Значение ш |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Значение L2, мм |
3,5 |
6,4 |
10,9 |
17,3 |
25,5 |
36,0 |
51,9 |
81,5 |
142,5 |
263 |
|
Значение L2ф, мм |
3,5 |
7,5 |
12,5 |
19,0 |
27,5 |
38,5 |
55,0 |
81,5 |
132,5 |
263 |
|
Относительная погрешность ε, % |
0,0 |
17,2 |
14,6 |
9,8 |
7,8 |
6,9 |
6,0 |
0,0 |
7,0 |
0,0 |
|
Среднее значение ε ср, % |
6,9 |
|||||||||
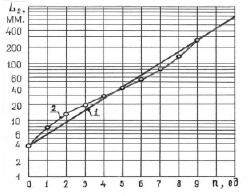
Рис. 4. Зависимость расстояния дифракционных максимумов L2 от их номера n (линия 2) по уравнению 6, точки – фактические значения (Lф). Линия 1 – экспонента в уравнении 6
Казалось бы, имея данные по дифракции гравитационных волн, можно определить их длину. Но для точного расчета недостаточно экспериментальных данных. Используем известную формулу дифракционной решетки: dsin φ = m λ (4), которая для оценочных расчетов вполне приемлема. Вероятно, дифракция гравитационных волн происходит на ядрах атомов. Принимая d ≈10-15 м, а sin φ = 1 (т.е. φ = 90º) при m = n = 14 из уравнения (4) получим: λ ≈ 10-17 м.
Выводы
Как следует из сопоставления результатов дифракции света, описываемых уравнением (5), и данных по расположению планет Солнечной системы (а по литературным источникам – и спутников этих планет), описываемых уравнением (3), эти уравнения абсолютно идентичны и оба описывают явление дифракции; только одно – (5), – дифракцию света, а другое – (3), по видимому, – дифракцию гравитационных волн, идущих от Солнца. На этом основании мы можем сделать вывод о том, что положение планет и других объектов Солнечной системы определяется положением максимумов дифракции гравитационного поля Солнца (аналогично – положение спутников и колец планетных систем определяется положением максимумов дифракции гравитационного поля планет).
Область возможного использования результатов. Экспериментальные космические исследования дифракционных минимумов и максимумов гравитационного поля. Объяснение устойчивости, происхождения и эволюции Солнечной системы и её планетных систем. Теория гравитационного поля. Методика аналогий в исследованиях.