Известно, что классическое дискретное преобразование Фурье (ДПФ) и его быстрые алгоритмы, выступают в качестве традиционного математического аппарата, который используется для анализа стационарных процессов. С практической точки зрения, в основу которой положено точное представление произвольных сигналов, ДПФ и быстрое преобразование Фурье (БПФ) имеют ряд недостатков. Устранить данные недостатки можно за счет перехода к крупномасштабной обработке сигналов с использованием вейвлет-преобразований.
Основная часть. При этом для обеспечения реального масштаба времени при построении вычислительных устройств цифровой обработки сигналов (ЦОС) во многом применялись специализированные процессоры (СП). Так в работах [1, 2] предлагается использовать в качестве математического аппарата цифровой обработки сигналов алгебраические структуры, обладающие свойством кольца и поля. Применение модулярных кодов системы остаточных классов (СОК) позволяет осуществлять параллельные вычисления по основаниям, в качестве которых используются взаимно простые числа.
Наряду с системой остаточных классов для организации ортогональных преобразований сигналов используются и другие непозиционные системы. В работах [3–8] приведены примеры применения полиномиальной системы классов вычетов (ПСКВ) в цифровой обработке сигналов. Эти коды позволяют эффективно осуществлять обработку данных в реальном масштабе времени за счет перехода от одномерной обработки сигналов к многомерной. Кроме этого коды ПСКВ эффективно реализуют алгоритмы, которые содержат операции сложения, вычитания и умножение. Следует отметить, что наряду с алгоритмами цифровой обработки сигналов, полиномиальная система классов вычетов нашли применение и в высокоскоростных системах шифрования потока данных [9].
Однако, отмеченные выше преобразования сигналов на основе ДПФ и его быстрых алгоритмов, имеют ряд недостатков. Данные преобразования имеют хорошую локализацию по частоте, при этом временное разрешение желает быть значительно лучше. Использование ДПФ и быстрого преобразования Фурье (БПФ) не учитывает ситуацию, когда частота колебаний может изменяться во времени. Отмеченных недостатков лишен математический аппарат крупномасштабной обработки сигналов вейвлет-преобразования [10].
Одним из наиболее используемых вейвлет-преобразований является преобразование Хаара. Данное преобразование является разделимым и может быть представлено в виде матриц
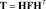, (1)
где F – матрица сигнала; H – матрица преобразования; T – результат преобразования сигнала.
Матрица преобразования Хаара включает в свой состав базисные функции Хаара hk(z).Отмеченные выше функции будут определяться на непрерывном замкнутом интервале z∈[0, 1]. Значение переменной k находятся в пределе от 0 до N-1, где N = 2n. При этом для каждого индекса k, определяется пара значений p и q, для которых справедливо,
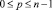, (2)
так чтобы выполнялось условие
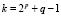. (3)
Значение индекса выбирается следующим образом
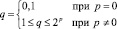(4)
Пусть N = 4. Определим значения индексов k, p и q. Так как значение n = 2, то согласно (2) параметр р принимает значения 0 и 1.
При k = 0 индексы принимают значения p =0 и q = 0.
При k = 1 индексы принимают значения p =0 и q = 1.
При k = 2 воспользуемся выражениями (3) и (4). Тогда индекс p =1 . Затем на основании (4) определяем, что значение может быть q = 1 или q = 2. Чтобы вычислить значение индекса q применяем условие (3). Получаем q = 1.
Поступаем аналогичным образом для вычисления индексов p и q для k = 3. В этом случае имеем q = 2.
Полученные значения индексов p и q позволяют осуществлять вычисление базисные функции Хаара. При k=0 получаем базисную функцию
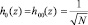, (5)
где z∈[0, 1].
Остальные базисные функции задаются выражением
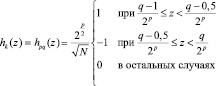, (6)
где z∈[0, 1].
Произведем расчет базисных функций Хаара с использованием (5) и (6) для N = 4. Согласно (5) получаем значения
.
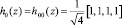При k = 1 индексы принимают значения p =1 и q = 1. Тогда согласно (6) для значения переменной z = {0, 0,25, 0,5, 0,75} имеем
В результате имеем строку матрицы вида
.
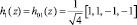При k = 2 индексы принимают значения p =1 и q = 1. Тогда согласно (6) для значения переменной z = {0, 0,25, 0,5, 0,75} имеем
В результате имеем строку матрицы вида
.
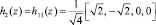При k = 3 индексы принимают значения p =1 и q = 2. Тогда согласно (6) для значения переменной z = {0, 0,25, 0,5, 0,75} имеем
В результате имеем строку матрицы вида
.
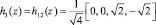Таким образом, матрица преобразования Хаара Н4 имеет вид
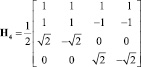
Проведем прямое преобразование Хаара для входной последовательности отсчетов сигнала f(x) = [0, 1, 2, 4]. Тогда согласно математического аппарата, который связан с крупномасштабной теорией, имеем
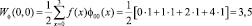
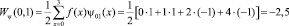
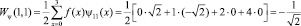
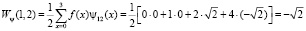
Таким образом, результатом вейвлет-преобразования имеем
.
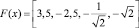Для того, чтобы восстановить исходный сигнал, воспользуемся следующей формулой
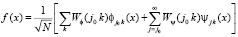. (7)
Произведем расчет восстановленных отсчетов исходного сигнала.
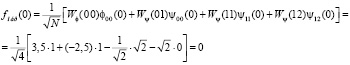
Аналогично находим первый отсчет восстановленного сигнала
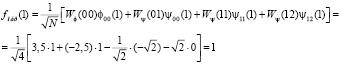
Второй отсчет восстановленного сигнала находим следующим образом
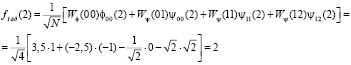
Значение третьего отсчета восстановленного сигнала находим следующим образом
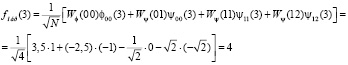
Таким образом, результатом обратного вейвлет-преобразования имеем последовательность вида
.
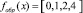Для выполнения обратного преобразования была использована транспонированная матрица Хаара Н4.
Проведенные исследования показали, что в качестве базовых операций, выполняемых при осуществлении прямого и обратного преобразований Хаара, использовались операции суммирования, вычитания и умножения. Это позволяет использовать коды системы остаточных классов. При построении таких кодов классов вычетов в качестве оснований применяются взаимно простые числа [1,2,10]. Благодаря этому любой позиционный код можно представить в виде набора остатков, полученных при делении этого числа на числа-основания
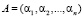, (8)
где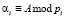 
; i = 1,…,n.
Рассмотрим выполнение арифметических операций в модулярном непозиционном коде. Представим значения остатков операндов в виде степеней двойки. Пусть для двоичной записи основания pi, i = 1,…,n, потребуется mi двоичных разрядов. Тогда остаток можно представить
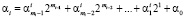. (9)
Соответственно для второго операнда получаем
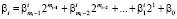. (10)
Так как сравнения по одному и тому же модулю можно почленно складывать, то для суммы двух чисел А и B, имеющих соответственно коды (a1, a2,…, an) и (b1, b2,…, bn) справедливы соотношения:
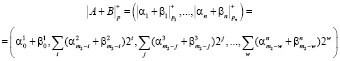, (11)
где + – операция суммирования по модулю р.
Аналогично получаем для операции вычитания в СОК
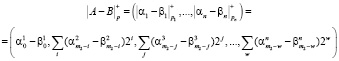, (12)
Как наглядно видно в равенствах (11) и (12) полученные подмножества образуют циклическую группу сложения по основаниям pi, I = 1,…,n, СОК. При этом каждая группа включает в себя конечное число элементов. Операция сложения и обратная ей – вычитание производятся по модулю р, так как данные подмножества образуют аддитивную циклическую группу.
В силу дистрибутивности операции умножения операндов над кольцом на элементы этого кольца относительно операции сложения имеем
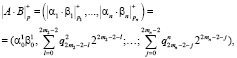(13)
где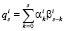 
– линейная свертка; s = 0,…, 2mi – 2; i = 0,…,n.
Таким образом, выполнение операции умножения над операндами в СОК согласно
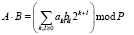, (14)
сводится к умножению соответствующих остатков по основаниям СОК с последующих суммированием по модулю характеристики поля.
Анализ выражений (11)-(15) показывает, что основным достоинством модулярных непозиционных кодов является сравнительная простота выполнения модульных операций (сложения, вычитания, умножения). Очевидно, что приведенные выше формальные правила выполнения операций в системе остаточных классов позволяют существенно повысить скорость выполнения крупномасштабных преобразований сигнала. При этом использование в качестве основания системы малоразрядные числа позволяет применять вычислительные устройства с заранее просчитанной детерминированной структурой.
Выводы
В работе рассмотрены вопросы применения вейвлет-преобразований для анализа сигнала. В качестве такого преобразования предлагается использовать преобразования Хаара. Приведены примеры прямого преобразования Хаара, а также реализация обратного преобразования. Показана возможность использования системы остаточных классов для реализации вейвлет-преобразования. Применение малоразрядных остатков позволит повысить скорость выполнения данного преобразования сигналов.