Модульное обучение в системе высшего образования уже многие годы доказывает свое преимущество, актуальность и успешность. Оно позволяет избежать многие проблемы изложения и изучения материала по всем дисциплинам. Традиционное изложение вузовского курса математики носит информационный характер, предполагает огромный объем новой информации, усвоение которой затрудняется в силу особенностей обучения в вузах технического профиля. Применение технологии модульного обучения применительно к строительным специальностям позволяет решить выделенные проблемы преподавания математики и является главным средством систематизации математических знаний студентов.
Перестройка процесса обучения по модульным программам позволяет:
1) интегрировать и дифференцировать содержание обучения путем группировки проблемных модулей учебного материала, обеспечивающих разработку курса математики в полном, сокращенном и углубленном вариантах;
2) осуществлять самостоятельный выбор учащимися того или иного варианта курса математики в зависимости от уровня обученности и обеспечивать индивидуальный темп продвижения по программе;
3) использовать модули в качестве сценариев для создания педагогических программных средств;
4) акцентировать работу преподавателя на консультативно-координирующие функции управления познавательной деятельностью учащихся:
5) сократить курс обучения без особого ущерба для полноты изложения и глубины усвоения учебного материала на основе адекватного комплекса методов и форм обучения.
Основополагающим этапом проектирования технологии модульного обучения математике является разработка модулей. Проектирование модулей, нацеленных на систематизацию математических знаний, базируется на, выделенных нами, дидактических принципах модульного обучения:
1. Принцип блочной структуры;
2. Принцип интегративности;
3. Принцип актуализации развивающего компонента содержания;
4. Принцип «незамкнутости»;
5. Принцип осознанной перспективы;
6. Принцип сотрудничества.
Рассмотрим реализацию данных принципов на примерах курса высшей математики в вузе. Каждый построенный блок модуля может быть логически и наглядно связан с предыдущим, образовывая новые единые блоки, при этом не нарушается последовательное изложение математического материала, происходит его выстраивание в единый блок математической теории (принцип блочной структуры). Покажем взаимосвязь всех модулей высшей математики, как известно первыми изучаются модули, являющиеся базовыми в остальных это «Линейная алгебра», «Аналитическая геометрия», «Математический анализ». Далее идет изучение производных, интегралов, ФНП, рядов все изучается в определенных модулях и существуют важные связи между ними. Изучение модулей «Теория вероятностей» и «Математическая статистика», идет после основ высшей математике, но и базируются на основе ее изучения. Из всего выше перечисленного нами разработана следующая блочная структура курса высшей математики:
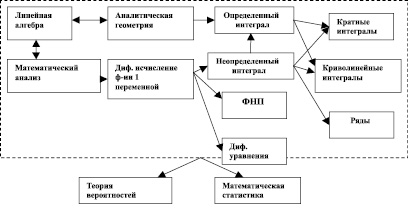
Каждый модуль содержит в себе несколько блоков, представляющих собой полную систему знаний по определенной теме (принцип интегративности). Приведем пример блочной структуры модуля «Ряды»:
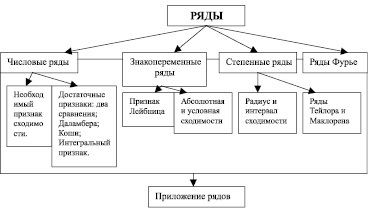
В каждом блоке предлагаются задачи, решение которых развивает у обучающихся способность использовать имеющиеся знания в новых ситуациях и закреплять их умениями (принцип актуализации развивающего компонента содержания). В качестве примера приведем одну из таких задач: вычислить интеграл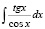 
:
а) с помощью универсальной тригонометрической подстановки;
б) с помощью частной тригонометрической подстановки;
в) внесением под знак дифференциала.
Затем проведем обсуждение способов решения с точки зрения рациональности.
а)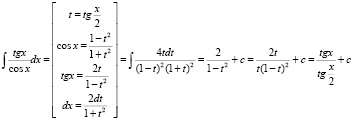 
;
б)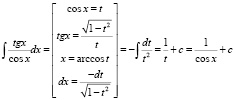 
;
в)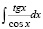 
.
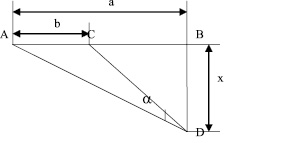
После нахождения интеграла тремя способами, студенты убеждаются, что последний наиболее короткий и рациональный.
Реализацию принципа «незамкнутости» можно видеть на следующем примере: в модуле «Ряды» предложить задачи, на исследование сходимости рядов, в которых при подсчете пределов нужно использовать правило Лопиталя, изученного в модуле «Дифференциальное исчисление функции одной переменной».
Обучающиеся должны четко знать для чего и зачем они изучают каждый модуль, чтобы осознанно пополнять систему своих математических знаний. Для этого должна быть проделана большая работа по мотивации, а также приложение в каждый модуль задач с практической направленностью для инженеров-строителей (принцип осознанной перспективы). Приведем пример такого рода задач:
Задача 1. Для придания консоли АB = a жесткости используются две опоры AD и CD (рисунок), где АB = b.
Наибольшая жесткость конструкции достигается при наибольшей величине угла a, тангенс которого определяется формулой: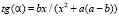 
. Определите, на каком расстоянии от точки B следует закрепить опоры, чтобы придать конструкции наибольшую жесткость.
Задача 2. Определить скорость подъема поднимаемой строительным краном бетонной плиты, зная, что скорость v(t) является первой производной от перемещения по времени. Зависимость высоты подъема плиты от времени описывается формулой h(t) = 0,02·t2 + 4.
Роль преподавателя-консультанта при модульном обучении подталкивает к сотрудничеству студента, это выражается и в подготовке к базовым занятиям, и к занятиям углубленного изучения, а также при отчетности по пройденным темам модуля (принцип сотрудничества).
Это лишь часть примеров реализации принципов модульного обучения по которым легко судить о их важности и применении на всех этапах изучения математики в вузе.