Для детерминистических модулярных структур в каждой ячейке структурированного 3D пространства состояния определяются возможными кристаллическими r, наноразмерными n и фрактальными f компонентами [1 – 10]. Квадратная матрица А третьего порядка вида
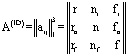
описывает множество вероятных структурных 1D состояний детерминистических модулярных структур композитов. Множество включает три основные состояния
(rrº r, nnº n, ffº f) и три пары из сопряженных (взаимодополняющих) состояний (rn и nr, rf и fr, nf и fn). Матрица А вероятных структурных 1D состояний обладает следующими свойствами:
1) равенство сопряженной и транспонированной матриц, т.е. А* = АТ,
2) равенство дважды сопряженной и дважды транспонированной матрицы – исходной матрице, т.е. (АТ)Т = (А*)* = А,
3) наличие частичного порядка соподчинения вида r ∈ fr ∈ nr, rn ∈ fn ∈ n
и rf ∈ f ∈nf.
Из десяти классов вероятных структурных состояний [1, 2]: (n n n), (n n r), (n n f), (n f f), (r f n), (r r n), (r r f), (r f f), (f f f)
и (r r r), – два класса характеризуют возможные структурные состояния, представители которых включают в себя одновременно кристаллическую и наноразмерную компоненты: ((r r n) и (n n r)). Возможные разложения данных состояний
3(n n r) = 2(n n n) + (r r r),
3(n r r) = (n n n) + 2(r r r),
(n n r) + (n r r) = (n n n) + (r r r)
позволяют рассматривать наряду с кристаллическими фазами наночастицы и могут служить аппроксимантами вероятных состояний на поверхности композиционных материалов и покрытий с антифрикционными свойствами, а также вблизи поверхности в зоне трения и износа.
Симметрия структур Rrnn3 и Rrrn3может описываться пространственными G33 , слоевыми G32, ленточными G32,1 группами [11]. Перечислим возможные виды состояний класса (r r n) и (r n n), приведем соподчиненные (∈) и сопряженные им (*) состояния.
Класс кристаллический наноразмерный (r r n):
1) (r r n) – 3D-структура из упорядоченных цепочек нанообъектов в 2D-пространстве, (r r n)* = (r r n), (r r n) ∈ (nr nr n),
2) (r r nr) – 3D-структура из упорядоченных цепочек кристаллических нанообъектов в 2D-пространстве, (r r nr)* = (r r rn),
(r r nr) ∈ (nr nr nr),
3) (r r nf) – 3D-структура из упорядоченных цепочек фрактальных нанообъектов в 2D-пространстве, (r r nf)* = (r r fn),
(r r nf) ∈ (nr nr nf),
4) (r rn n) – 3D-структура из 1D-фрагментов нанообъектов, (r rn n)* = (r nr n), (r rn n) ∈ (nr n n),
5) (r rn nr) – 3D-структура из 1D-фрагментов кристаллических нанообъектов,
(r rn nr)* = (r nr rn), (r rn nr) ∈ (nr n nr),
6) (r rn nf) – 3D-структура из 1D-фрагментов фрактальных нанообъектов, (r rn nf)* = (r nr fn), (r rn nf) ∈ (nr n nf),
7) (r rf n) – 3D-структура из нанообъектов, упорядоченных по фрактальному и кристаллическому закону (r rf n)* = (r fr n), (r rf n) ∈ (nr nf n),
8) (r rf nr) – 3D-структура из кристаллических нанообъектов, упорядоченных по фрактальному и кристаллическому закону, (r rf nr)* = (r fr rn), (r rf nr) ∈ (nr nf nr),
9) (r rf nf) – 3D-структура из фрактальных нанообъектов, упорядоченных по фрактальному и кристаллическому закону, (r rf nf)* = (r fr fn), (r rf nf) ∈ (nr nf nf).
10) (rn rn n) – 3D-структура из 1D-фрагментов нанообъектов, упорядоченных в 2D-пространстве, (rn rn n)* = (nr nr n),
(rn rn n) ∈ (n n n),
11) (rn rn nr) – 3D-структура из 1D-фрагментов кристаллических нанообъектов, упорядоченных в 2D-пространстве,
(rn rn nr)* = (nr nr rn), (rn rn nr) ∈ (n n nr),
12) (rn rn nf) – 3D-структура из 1D-фрагментов фрактальных нанообъектов, упорядоченных в 2D-пространстве,
(rn rn nf)* = (nr nr fn), (rn rn nf) ∈ (n n nf),
13) (rn rf n) – 3D-структура из нанообъектов, упорядоченных по фрактальному закону в 1D-пространстве, (rn rf n)* = (nr fr n), (rn rf n) ∈ (n nf n),
14) (rn rf nr) – 3D-структура из кристаллических нанообъектов, упорядоченных по фрактальному закону в 1D-пространстве,
(rn rf nr)* = (nr fr rn), (rn rf nr) ∈ (n nf nr),
15) (rn rf nf) – 3D-структура из фрактальных нанообъектов, упорядоченных по фрактальному закону в 1D-пространстве,
(rn rf nf)* = (nr fr fn), (rn rf nf) ∈ (n nf nf).
16) (rf rf n) – 3D-структура из нанообъектов, упорядоченных по фрактальному закону в 2D-пространстве, (rf rf n)* = (fr fr n),
(rf rf n) ∈ (nf nf n),
17) (rf rf nr) – 3D-структура из кристаллических нанообъектов, упорядоченных по фрактальному закону в 2D-пространстве,
(rf rf nr)* = (fr fr rn), (rf rf nr) ∈ (nf nf nr),
18) (rf rf nf) – 3D-структура из фрактальных нанообъектов, упорядоченных по фрактальному закону в 2D-пространстве, (rf rf nf)* = (fr fr fn), (rf rf nf) ∈ (nf nf nf).
Класс наноразмерный кристаллический (r n n):
1 (r n n) – 3D-структура из упорядоченных 2D наночастиц, (r n n)* = (r n n),
(r n n) ∈ (nr n n),
2) (r n nr) 3D-структура упорядоченных 2D нанофрагментов структуры, (r n nr)* = (r n rn), (r n nr) ∈ (nr n nr),
3) (r n nf) – 3D-структура из упорядоченных 2D локальных фракталов, (r n nf)* = (r n fn), (r n nf) ∈ (nr n nf),
4) (r nr nr) – 3D-структура из упорядоченного 2D нанофрагмента структуры,
(r nr nr)* = (r rn rn), (r nr nr) ∈ (nr nr nr),
5) (r nr nf) – 3D-структура из упорядоченного нанообъекта из 1D-фрагмента структуры и 1D локального фрактала, (r nr nf)* = (r rn fn),
(r nr nf) ∈ (nr nr nf),
6) (r nf nf) – 3D-структура из упорядоченного 2D локального фрактала, (r nf nf)* = =(r fn fn), (r nf nf) ∈ (nr nf nf),
7) (rn n n) – 3D-структура из 2D наночастиц и упорядоченных в 1D-пространстве нанофрагментов, (rn n n)* = (nr n n),
(rn n n) ∈ (n n n),
8) (rn n nr) – 3D-структура из 1D наночастиц и 1D нанофрагментов структуры, упорядоченных в 1D-пространстве, (rn n nr)* = =(nr n rn), (rn n nr) ∈ (n n nr),
9) (rn n nf) – 3D-структура из 1D наночастиц и 1D локальных фракталов, упорядоченных в 1D-пространстве нанофрагментов (rn n nf)* = (nr n fn), (rn n nf) ∈ (n n nf),
10) (rn nr nr) – 3D-структура из 2D нанофрагментов структуры, упорядоченных в 1D-пространстве, (rn nr nr)* = (nr rn rn),
(rn nr nr) ∈ (n nr nr),
11) (rn nr nf) – 3D-структура из 1D нанофрагментов структуры и 1D локального фрактала, упорядоченных в 1D-пространстве,
(rn nr nf)* = (nr rn fn), (rn nr nf) ∈ (n nr nf),
12) (rn nf nf) – 3D-структура из 2D локальных фракталов, упорядоченных в 1D-пространстве нанофрагментов (rn nf nf)* = (nr fn fn), (rn nf nf) ∈ (n nf nf),
13) (rf n n) – 3D-структура из 2D наночастиц, упорядоченных в 1D-пространстве по фрактальному закону, (rf n n)* = (fr n n),
(rf n n) ∈ (nf n n),
14) (rf n nr) – 3D-структура из 1D наночастиц и 1D нанофрагментов структуры, упорядоченных в 1D-пространстве по фрактальному закону, (rf n nr)* = (fr n rn),
(rf n nr) ∈ (nf n nr),
15) (rf n nf) – 3D-структура из 1D наночастиц и 1D локальных фракталов, упорядоченных в 1D-пространстве по фрактальному закону, (rf n nf)* = (fr n fn), (rf n nf) ∈ (nf n nf),
16) (rf nr nr) – 3D-структура из 2D нанофрагментов структуры, упорядоченных в 1D-пространстве по фрактальному закону, (rf nr nr)* = (fr rn rn), (rf nr nr) ∈ (nf nr nr),
17) (rf nr nf) – 3D-структура из 1D нанофрагментов структуры и 1D локального фрактала, упорядоченных в 1D-пространстве по фрактальному закону, (rf nr nf)* = (fr rn fn),
(rf nr nf) ∈ (nf nr nf),
18) (rf nf nf) – 3D-структура из 2D локальных фракталов, упорядоченных в 1D-пространстве по фрактальному закону, (rf nf nf)* = (fr fn fn), (rf nf nf) ∈ (nf nf nf).
Таким образом, 36 видов реализации состояний класса (r r n) и (r n n) включают в себя все 10 видов соподчиненных им состояний наноразмерного класса (n n n) и имеют сопряженные с ними разновидности состояний всех остальных восьми классов.
Условный размерный параметр D для каждого структурного состояния может быть рассчитан по одному из его возможных разложений следующим образом: D = dr D(r) + df D(f) + dn D(n), где dr, df и dn – количества соответствующих компонент одного сорта, условный размерный параметр для кристаллической компоненты D(r) = 1, для фрактальной компоненты он полностью совпадает с фрактальной размерностью: D(f) = DimRf = Dim (GenRf) < 1, для наноразмерной компоненты D(n) = (<n>/no) < 1, если средний размер нанообъекта <n> < no = =100 нм и D(n) = 1, если <n>³ no.
Пример. Определим размерный параметр для 18-ой разновидности состояния: (rf nf nf) – 3D-структуры из 2D локальных фракталов, упорядоченных в 1D-пространстве по фрактальному закону. Сопряженным с ним состоянием является состояние
(fr fn fn), представляющее собой 3D-структуру из 1D детерминистических фракталов и 2D фрактальных нанообъектов. С учетом разложения (rf nf nf) = 1/6 [(r r r)+3(f f f)+2(n n n)] окончательно получим
D = 1/6 [3 + DimGenRfff1 + DimGenRfff2 + +DimGenRfff3 + 6(<n>/no)] < 3.
Будем считать, что величина условного размерного параметра оказывает функциональное влияние на чувствительные к особенностям структурной организации свойства систем, т.е. Si(Di). Предположим, что характер этого влияния может определяться для i-го структурного состояния зависимостями типа Si(d-Di). В этом случае на свойство SD влияет отклонение условного размерного параметра D от мерности пространства d, т.е. величина |d-D|. Формально можно рассматривать два вида зависимостей: SD = Sd(1 + K|d-D|) и ln(SD/Sd) = K|d-D|, в которых К – коэффициент пропорциональности, обусловленный как характеристиками структурного состояния, так и характеристиками пространства существования системы с данным состоянием. При расчете размерных параметров структурных состояний для отдельных компонент использовали следующие условные значения: D(r) = 1, D(f) = 0,5, D(n) = 0,1. Очевидно, что вторая зависимость от размерного параметра – экспоненциальная SD = Sd exp(K|d-D|) является более сильной по сравнению с первой (рисунок).
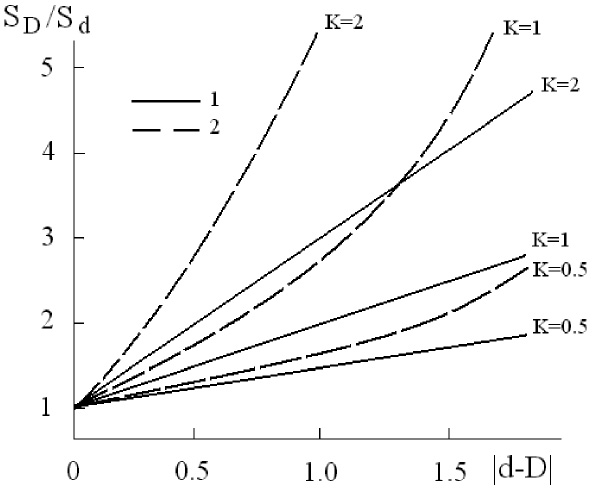
Влияние условного размерного параметра D структурного состояния детерминистических модулярных структур на свойства систем по зависимостям вида
SD = Sd(1 + K|d-D|) (1) и SD = Sd exp(K|d-D|) (2)
Ранее представления о возможном влиянии комплексного состояния композитов, обусловленного как кристаллическими фазами, так и распределенными определенным образом наночастицами некоторых из этих фаз были использованы при целенаправленном поиске и интерпретации трибологических свойств поверхности композиционных материалов и покрытий на основе систем Ni-P и Ni-B [12–20].



