Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Вероятность столкновения астероида 99942 Апофис с Землёй оценивается специалистами как достаточно низкая. Однако почти не рассматривается одна сопутствующая опасность, связанная с прохождением большого астероида вблизи Земли. Не исключено наличие меньших по размеру спутников астероида 99942 Апофис, столкновение с которыми может стать абсолютной неожиданностью из-за отсутствия информации об этих объектах. При этом они могут привести если не к глобальной катастрофе, то к крупным региональным катастрофам в зонах столкновения. В связи с этим может быть опасен не только сам астероид 99942 Апофис, но и его спутники.

Спутники астероидов являются не редким явлением. Именно они могут представлять дополнительную опасность для различных районов поверхности Земли. Проблема осложняется тем, что из-за малых размеров спутников астероида, их визуальное наблюдение затруднено, информация о них неполная и предсказать район их падения ещё сложнее. Новейшие исследования показывают, что астероиды могут не являться сплошным твёрдым телом, а обладать рыхлой структурой [1]. Таким образом, из-за собственного вращения астероида или его соударения с другими более мелкими телами, возможно появление новых спутников астероида, что делает проблему ещё более актуальной. Более того, специалисты отмечают, что «Исследование динамики астероидов, сближающихся с большими планетами, представляет собой сложную задачу по ряду причин. Во-первых, начальные данные астероидов определяются из наблюдений и поэтому известны не точно. Во-вторых, при численном интегрировании уравнений движения астероидов во время сближений с большими планетами может происходить значительное падение точности» [2]. Исследование динамики поведения орбит астероидов при движении вблизи планеты представляет собой сложную задачу; начальные данные спутников астероидов известны ещё менее точно, вследствие их малых размеров и меньшей доступности для наблюдения. Поэтому поведение системы «астероид – спутник» при сближении с планетой требует отдельного теоретического исследования. Сразу оговорим, что в работе речь будет идти не о двойных астероидах. Двойным астероидом называют астероидную систему, в которой размеры спутника сопоставимы c размером астероида. В данной работе будет проводиться исследование спутников, размеры и масса которых кратно меньше основного астероида.

В 2013 году, во время сближения Земли с астероидом 367943 Дуэнде (старое название 2012DA14), за 16 часов до максимального сближения, недалеко от Челябинска упал крупный метеорит. Ударная волна от метеорита вызвала разрушения в городе, это был первый в истории нынешней цивилизации случай таких массовых повреждений при падении метеорита в жилой зоне. Часть специалистов придерживалась версии, что метеорит в Челябинске был спутником астероида 367943 Дуэнде, однако всё же многие исследователи считают, что это случайное совпадение. Как правило, спутники астероидов находятся на расстоянии до 20.000 км. от основного объекта, тогда как в случае астероида 367943 Дуэнде и челябинского метеорита остаётся непонятным слишком большое расстояние между двумя объектами (500 тыс.км), в связи с чем большинство учёных отвергали их взаимосвязь. Большинство исследователей, в том числе Европейское космическое агентство и NASA, опровергли связь между этими событиями, обратив внимание на 2 аспекта:

1. Различные траектории движения объектов (челябинский болид двигался с востока на запад, в то время как расчётная траектория астероида 367943 Дуэнде проходила с юга на север)

2. Значительное расстояние между объектами (около 500 тыс. км).

На официальном сайте НАСА утверждается, что между челябинским метеоритом и астероидом 367943 Дуэнде не было никакой взаимосвязи [3]. Поэтому есть все основания полагать, что на данный момент отсутствуют работы, в которых было бы доказано, что метеорит в Челябинске был спутником астероида 367943 Дуэнде.

Разнятся оценки как размера и массы астероида 367943 Дуэнде, так и метеорита в Челябинске. В некоторых источниках приведены данные 17 метров и 10.000 тонн [4]. Параметры астероида 367943 Дуэнде также разнятся от 30 метров и 40.000 тонн до 40 метров и 130.000 тонн. Всё это, конечно, препятствует построению точных моделей, которые могли бы воспроизвести события 15-16 февраля 2013 года и дать полный ответ на вопрос о взаимосвязи двух объектов. Однако, тем не менее, это не препятствует проведению исследования некоторых общих свойств системы «астероид – спутник» с использованием абстрактных моделей.

Приливное воздействие на систему тел и деформация орбит. Объяснение расстояния между объектами

Большинство исследователей, отвергающие связь двух объектов, неявно исходят из предположения, что расстояние между астероидом и его спутником при приближении к крупной планете остаётся примерно таким же, как при полёте в межпланетной среде, и делают вывод об отсутствии взаимосвязи [3]. Однако на самом деле орбита спутника астероида при воздействии гравитации планеты неизбежно претерпевает деформацию, эксцентриситет увеличивается, орбита вытягивается в сторону тяготеющей массы, значительно превосходящей как астероид, так и его спутник. Аналогичные процессы мы видим также и в системе трёх тел «Солнце, Земля, Луна». Орбита Луны не является круглой, а вытянута в сторону Солнца. Во время новолуния расстояние принимает значения около 405 тыс. км, а во время полнолуния около 360 тыс.км. Земля со своим спутником существуют в гравитацоннном поле Солнца, что накладывает влияние на орбиту спутника. Этот процесс фактически является приливным воздействием тяготеющей массы на систему, состоящую из космического тела и его спутника. Приливное воздействие может оказываться как на отдельно взятое космическое тело, так и на систему тел. В случае одного тела, например, планеты, приливное воздействие происходит вследствие разности расстояний от тяготеющей массы до разных точек планеты, и выражается в деформации планеты. В случае системы тел, эффект приливного воздействия определяется диаметром орбиты спутника, и выражается в искажении орбиты.

Оценим вероятность того, что спутник астероида находится ближе к Земле, чем астероид, в зависимости от эксцентриситета орбиты спутника. Так как, по известным законам Кеплера, за равные промежутки времени образуются равные площади секторов эллипса, достаточно оценить площадь доли эллипса, расположенной правее левого фокуса, по отношению ко всей площади эллипса.

Влияние гравитационных сил со стороны планеты неизбежно деформирует орбиту спутника астероида, увеличивая её эксцентриситет. Таким образом, при приближении к планете, орбита спутника астероида становится сильно вытянутой, и спутник проводит наибольшую часть времени между планетой и астероидом. Вероятность нахождения спутника впереди астероида при приближении к крупному телу, такому как планета, всегда больше 0,5 и лишь увеличивается по мере приближения к планете. Следовательно, в этот период времени большинство мелких частиц будут опережать астероид, а не следовать за ним.

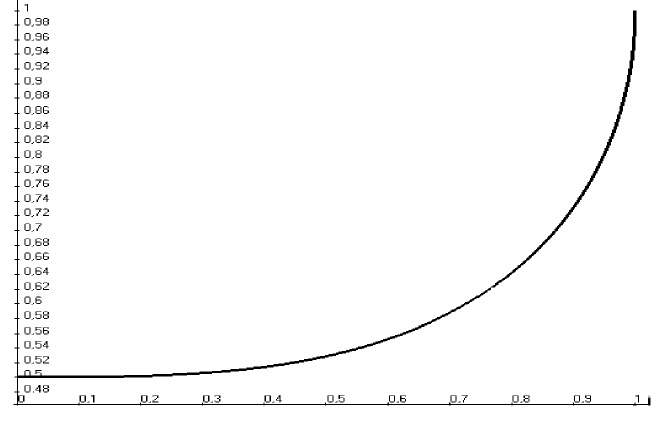
Рис. 1. Зависимость вероятности нахождения спутника впереди, а не позади астероида, в зависимости от эксцентриситета его орбиты (от 0 до 1)

При приближении астероида к крупной планете происходит неизбежная деформация орбиты спутника под воздействием гравитационных сил со стороны планеты. При движении спутника астероида по орбите, обладающей значительным эксцентриситетом, основную часть времени оборота вокруг астероида он будет находиться ближе к планете, то есть между астероидом и планетой. При приближении к планете, время опережающего нахождения будет становиться всё больше.

При достижении определённого критического расстояния, гравитационные силы со стороны планеты становтся больше, чем со стороны астероида, спутник перестаёт быть спутником астероида и начинает опережающее приближение к планете. Так, если масса астероида 367943 Дуэнде оценивается в  кг, то при приближении к системе, состоящей из Земли и Луны, общей массой около кг, соотношение масс приблизительно ,
таким образом, достаточно соотношения расстояний , чтобы сила притяжения к планете превысила силу притяжения к астероиду. Таким образом, например, для расстояния между спутником и астероидом в 25 м., этот эффект начнёт проявляться уже на расстоянии 5 млн. км.: спутник перестаёт вращаться вокруг астероида и начинает приближаться к планете с чуть большей скоростью, чем астероид. При этом, из-за разницы в расстояниях до планеты, скорость бывшего спутника возрастает быстрее, чем скорость самого астероида, поэтому спутник оказывается возле планеты раньше. Наиболее вероятно, что именно этим и объясняется столь значительное расстояние между астероидом 367943 Дуэнде и метеоритом на момент падения метеорита вблизи Челябинска. С большой вероятностью метеорит будет опережать астероид на расстояние, значительно превышающее тот радиус орбиты спутника, который имел место до приближения к планете. Таким образом, при неглубоком рассмотрении будет ошибочно казаться, что эти объекты не были взаимосвязаны, как и произошло в случае метеорита в Челябинске. Аномально большое расстояние между астероидом 367943 Дуэнде и его спутником оказывается вполне объяснимо. Итак, как видно, расстояние не является доводом в пользу отсутствия взаимосвязи этих объектов.

Объяснение разных
траекторий объектов

Теперь рассмотрим довод о несоответствии траекторий. Траектория спутника астероида после захвата гравитационным полем Земли может изменяться совершенно непредсказуемым образом, в частности, спутник, попавший в гравитационное поле планеты, может упасть не сразу, а приближаться по закручивающейся спирали. Таким образом, его траектория после выхода из гравитацонного поля астероида более не связана с траекторией полёта астероида. В процессе сближения, спутник может совершить часть оборота вокруг планеты и войти в атмосферу на другой стороне планеты, с противоположной стороны от приближающегося астероида. Это вовсе не означает, что он не был связан с астероидом ранее.

Приведённые на официальной странице НАСА [3] чертежи траектории челябинского метеорита нельзя считать достоверными, так как объект был обнаружен лишь в самый последний момент, при вхождении в атмосферу, был ранее неизвестен и не наблюдался абсолютно никем из астрономов. Таким образом, его траектория до вхождения в атмосферу могла быть лишь приблизительно экстраполирована на предшествующий момент времени, и не исключено, что объект приближался к Земле по закручивающейся спирали со стороны астероида 367943 Дуэнде, а не по той траектории, которая приводится на сайте НАСА. Разброс траекторий мелких частиц, вырванных планетой из гравитационного поля астероида и движущихся к планете с ускорением, может быть весьма велик, и они могут войти в атмосферу в любой точке. Есть и другие подтверждения данной гипотезе. Астероид 367943 Дуэнде сопровождался не одним, а несколькими спутниками. За сутки до падения челябинского метеорита, болид был зафиксирован над Японией [5], а за два часа – наблюдался яркий болид на Кубе, от которого пострадало несколько строений [6].

Итак, оба прежних довода в пользу отсутствия взаимосвязи между двумя объектами сомнительны и не доказывают отсутствие взаимосвязи. Выявлено, что с наибольшей вероятностью спутники опережают астероид, а не следуют после него, то есть столкновения следует ожидать именно в то время, когда астероид ещё не приблизился на минимальное расстояние.

Моделирование и численные эксперименты

Автором было проведено численное моделирование поведения системы, состоящей из материального тела и его спутников, при отсутствии и в присутствии в окрестности системы более массивного космического тела. Было смоделировано движение спутников космического тела под воздействием второго тела кратно большей массы. Вокруг первого тела вращение происходило изначально, а вторая масса находилась на определённом расстоянии или приближалась к системе, состоящей из первого тела и его спутников. Начальные положения и начальные скорости спутников были заданы таким образом, чтобы при отсутствии другого космического тела орбиты спутников были близки к круговым. Вычислительные эксперименты показали, что приливные деформации орбит спутников имеют место и становятся причиной значительного удаления спутников от астероида. Более того, спутники могут быть захвачены гравитационным полем планеты ещё в процессе приближения, до момента максимального сближения. Тот факт, что точные параметры многих астероидов и их спутников неизвестны, не препятствует построению абстрактной «идеальной модели», описывающей свойства системы «астероид – спутник» при наличии на некотором расстоянии от системы более массивного космического тела.

При проведении серий экспериментов с вариативным заданием массы второго объекта и расстояния до него, измерялось максимальное удаление спутника от астероида. Радиус исходной орбиты соответствует единице. При наличии второго космического тела происходят приливные деформации орбиты спутника. Орбита перестаёт быть близкой к круговой, но при этом спутник ещё остаётся в гравитационном поле астероида, если второе тело расположено на достаточно далёком расстоянии или имеет недостаточную массу. Максимальное итоговое зафиксированное удаление спутника от астероида увеличивается, как правило, монотонно при изменении двух вводимых параметров – при увеличении массы второго космического тела либо при уменьшении расстояния до него. При увеличении массы выше некоторого критического значения, или при снижении расстояния ниже некоторого порога, отмечено значительное удаление от астероида (практически сравнимое с расстоянием до второй массы). Это означает, что происходит захват спутника гравитационным полем второго космического тела и опережающий полёт спутника по направлению к этому телу. Итоговое максимальное удаление от первого тела (астероида) может и превышать расстояние от астероида до второго тела: это означает, что из-за приобретённой скорости спутник пролетает мимо тяготеющей массы. При отсутствии второй массы, орбита почти круговая, имеющая радиус, равный 1 условной единице (удаление на величину 0,7 % радиуса орбиты соответствует крайне малым значениям эксцентриситета). Рассмотрим таблицу 1. Здесь m – масса первого объекта (астероида), m2 – кратная масса второго объекта, l – исходный радиус орбиты спутника при движении вокруг астероида. Максимальное удаление представлено в условных единицах, одна единица равна радиусу исходной орбиты спутника. Не выделенные серым цветом элементы таблицы соответствуют случаям, когда происходит деформация орбиты, но всё же спутник не покидает орбиту вокруг астероида. Выделенные элементы соответствуют ситуациям за пределами некоторого критического порога, когда спутник удаляется от первого объекта, так как притянут гравитационным полем второго объекта.

Зависимость максимального удаления спутника от астероида
при наличии на определённом расстоянии более массивного тела

В последних строках таблицы отмечено некоторое нарушение монотонной зависимости от изначально задаваемого расстояния. Здесь имеет место проявление следующего процесса. Если при захвате спутника гравитационным полем второго объекта, этот второй объект кратной массы (условная планета) находится на чуть более далёком расстоянии, то притягиваемый спутник, летящий к ней, за время полёта успевает развить более высокую скорость, и за счёт этого может пролететь мимо и удалиться более значительно. К тому же, столкновение не обязательно происходит, так как траектория полёта не всегда направлена прямо к планете, а подвержена вариациям в зависимости от начального положения и скорости спутника.

При приближении более массивного тела к системе, всегда имеют место деформации орбит спутников, причём для внешних спутников, изначально находившихся на большем расстоянии, чем остальные, эти деформации проявляляются раньше и сильнее. Орбиты спутников вытягиваются в сторону приближающейся массы, это фактическое проявление приливного воздействия массивного тела на систему «астероид – спутник». При достижении некоторого порогового значения параметров, наблюдается значительная нестабильность, спутник выходит из гравитационного поля астероида, далее движется ко второй массе, пролетает мимо второй массы за счёт значительной приобретённой во время приближения к ней скорости. В реальных условиях, а не абстрактной модели с точечными массами, приближение спутника к планете на слишком малое расстояние приведёт к его торможению и разогреву в верхних слоях атмосферы, а затем падению на планету. Вероятность столкновения не прямо пропорциональна массе планеты: при большой массе планеты бывший спутник астероида развивает более значительную скорость и может пролететь мимо.

Кроме вычисления удаления спутника от астероида, было сделано и графическое представление орбит. Рассмотрены три спутника, изначально находившиеся на разном расстоянии от астероида. При отсутствии второй массы, их орбиты близки к круговым, а при наличии второй массы вытягиваются в сторону этой массы (см. рис. 2).

Рис. 2. Приливные деформации траекторий трёх спутников,
вытянутые в сторону тяготеющей массы (масса справа)

При прохождении астероида вблизи более крупной массы, орбиты спутников подвергаются хаотическим изменениям, какой-либо из спутников астероида может быть захвачен гравитационным полем планеты и стать спутником планеты. Также в ряде численных экспериментов отмечено следующее явление. Под влиянием крупного тела, проходящего мимо системы, спутник описывает петлю и начинает обратное вращение вокруг исходного тела, по часовой стрелке, а не против.

Данные численные эксперименты позволяют сказать, что, вероятнее всего, такие изменения орбит возможных спутников астероида 367943 Дуэнде могли происходить при его сближении с Землёй в феврале 2013 года. Таким образом, Челябинский метеорит, а также болиды, зафиксированные над Японией и Кубой [5], [6] вполне вероятно, до того были одними из спутников астероида 367943 Дуэнде. Не исключено наличие и других спутников, которые за счёт приобретённой скорости пролетели мимо Земли и не столкнулись с ней.

Тот факт, что все три события произошли до, а не после сближения с астероидом 367943 Дуэнде, является не случайным, а вполне закономерным. Приливные деформации орбит в системе «астероид – спутник» таковы, что орбиты вытягиваются в сторону планеты, а значит, имеется значительная вероятность захвата спутников гравитационным полем планеты и опережающее приближение спутников по сравнению с астероидом. В большинстве случаев спутники могут столкнуться с планетой именно до, а не после прохождения основного астероида.

Выводы

1. При приближении астероида со спутниками к крупному космическому телу орбиты спутников деформируются, далее спутники могут быть захвачены гравитационным полем планеты и продолжить движение уже не как спутники астероида.

2. При приближении к Земле крупного астероида, его спутники, если они существуют, будут не следовать позже астероида, а опережать основной астероид на несколько часов, находясь на расстоянии, значительно превышающем обычное расстояние между спутниками и астероидом.

3. Челябинский метеорит до приближения к Земле ранее был спутником астероида 367943 Дуэнде.

4. Траектория спутника астероида после захвата гравитационным полем планеты может изменяться совершенно непредсказуемым образом и может быть уже не связана с траекторией полёта астероида. Это не означает, что объект не был связан с астероидом ранее.

5. В случае реализации проекта искусственного раздробления астероида, угрожающего Земле, на мелкие осколки, многие из них продолжат движение, вращаясь вокруг общего центра масс, будут захвачены гравитационным полем Земли и столкнутся с Землёй с гораздо большей вероятностью, чем столкнулся бы сам астероид.

6. При сближении любого крупного астероида с Землёй, в частности, при приближении астероида 99942 Апофис, также есть опасность столкновения с его спутниками, которые будут притянуты Землёй, причём наиболее высока вероятность региональных катастроф из-за таких столкновений именно в течение суток до максимального сближения с астероидом, а не после него.