Многие химические применения мёссбауэровской спектроскопии используют чувствительность мёссбауэровских параметров от изменения электронной плотности на ядре [1]. Изомерный сдвиг является функцией атомных и электронных свойств молекулярных систем, которые объединены таким образом, что независимая количественная информация по этим свойствам, не может быть получена только методом мёссбауэровской спектроскопии.
Так как электронные свойства, как правило, представляют интерес, и потому, что ядерные параметры постоянны, параметры сверхтонкого взаимодействия наиболее часто используются для сравнения электронных свойств различных молекул. Эффекты ковалентности и экранирование одного набора электронов другим также влияют на электронное окружение ядра и могут быть отражены в изменениях изомерного сдвига [2].
Мёссбауэровский изомерный сдвиг (δ) возникает из-за электростатического взаимодействия между ядерными и электронными зарядами вследствие конечного размера ядра. Выражение δ является функцией обоих изменениями радиуса ядра из-за ядерных переходов, и плотности электронов на ядре ρ(0) [1].
Изменение плотности электронов на ядре может быть связано с изменениями локальной электронной структуры, которые сильно зависят от окружения. Таким образом, вариации мёссбауэровского изомерного сдвига для ряда соединений того же элемента предоставляет ценную информацию об изменениях в химической связи [3].
Целью данной работы является создание достаточно простой интерпретации наблюдаемых основных тенденций в изменениях δ для обычных и донорно-акцепторных комплексов соединений металлов на основе расчета ρ(0) методами теории функционала плотности.
Матьериалы
и методы исследования
Геометрические структуры исследованных соединений были оптимизированы методом градиентной коррекции функционала плотности с помощью обменно-корреляционного потенциала, предложенного Becke в сочетании с обменным потенциалом LYP (B3LYP) [4] в рамках программы GAUSSIAN’03 [5].
Использование все электронного базисного набора DGDZVP для всех атомов позволяет получать достаточно надежные результаты [6]. Оптимизированные структуры молекул были далее использованы для расчета электронной плотности на ядре с использованием программного пакета Амстердамский функционал плотности [7].
Мы использовали обменный OРТX обменный функционал в сочетании с PBE корреляционным функционалом в базисе TZ2P+ с использованием приближения замороженного остова для учета внутренних электронов [8].
Релятивистские эффекты для всех атомов были учтены в рамках регулярного приближения нулевого порядка (ZORA), что позволяет более надежно описать близкое к ядру пространство, чем в приближении используемого формализма Паули [9]. Эти результаты были использованы нами ранее для расчета геометрических параметров, констант квадрупольного взаимодействия, вращательных постоянных, вибрационных частот и данных мессбауэровских спектров [10-12].
Результаты исследования
и их обсуждение
Основные наблюдаемые тенденции в изменении Мёссбауэровских изомерных сдвигов для соединений 119Sn, 121Sb, 127I, 131Xe, 197Au, 195Pt, 187Os, 57Fe, 193Ir интерпретируются в терминах валентных электронных заселенностей, и связаны с изменениями локального окружения ядер металлов [13]. Эти серии соединений соответствуют различным диапазонам экспериментальных значений δ, которые были соотнесены с рассчитанными значениями ρ(0) и валентными электронными заселенностями орбиталей атомов металлов (рис. 1-10). Все экспериментальные изомерные сдвиги были взяты из работы [14].
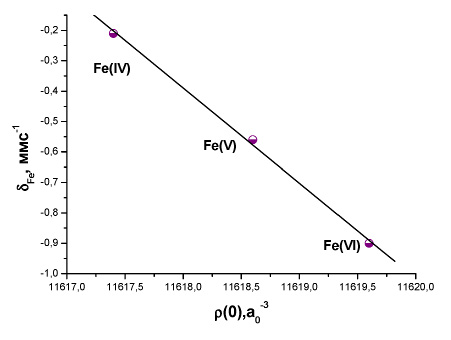
Рис. 1. Зависимость между экспериментальным изомерным сдвигом и рассчитанной методом BP86/TZ2P+ электронной плотностью на ядре 57Fe
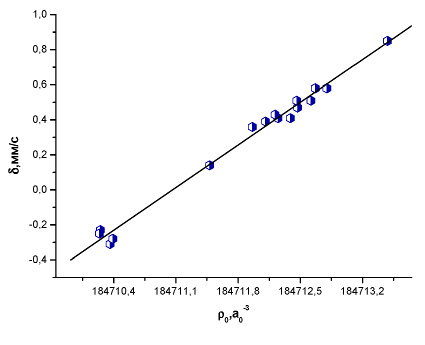
Рис. 2. Зависимость между экспериментальным изомерным сдвигом и рассчитанной методом BP86/TZ2P+ электронной плотностью на ядре 119Sn
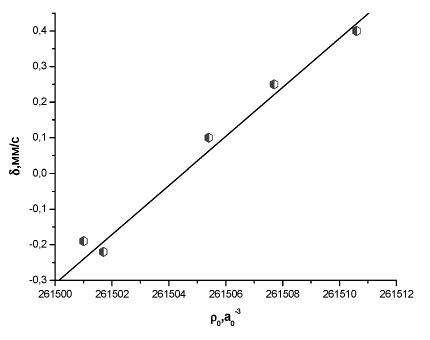
Рис. 3. Зависимость между экспериментальным изомерным сдвигом и рассчитанной методом BP86/TZ2P+ электронной плотностью на ядре 131Xe
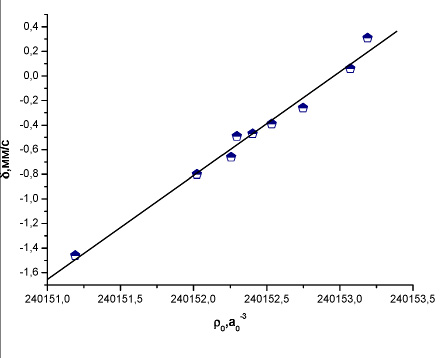
Рис. 4. Зависимость между экспериментальным изомерным сдвигом и рассчитанной методом BP86/TZ2P+ электронной плотностью на ядре 127I
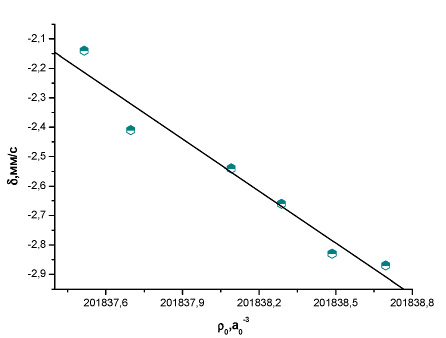
Рис. 5. Зависимость между экспериментальным изомерным сдвигом и рассчитанной методом BP86/TZ2P+ электронной плотностью на ядре 121Sb
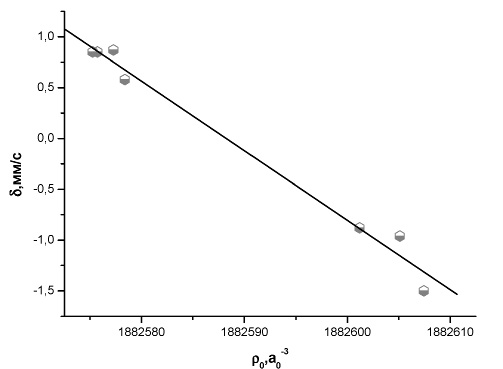
Рис. 6. Зависимость между экспериментальным изомерным сдвигом и рассчитанной методом BP86/TZ2P+ электронной плотностью на ядре 195Pt
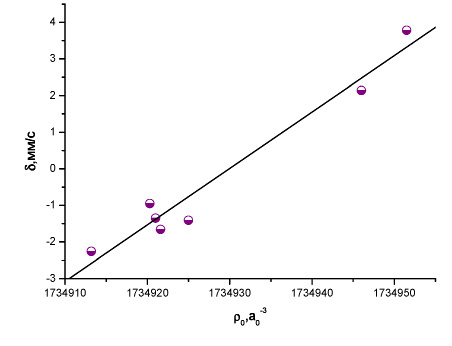
Рис. 7. Зависимость между экспериментальным изомерным сдвигом и рассчитанной методом BP86/TZ2P+ электронной плотностью на ядре 193Ir
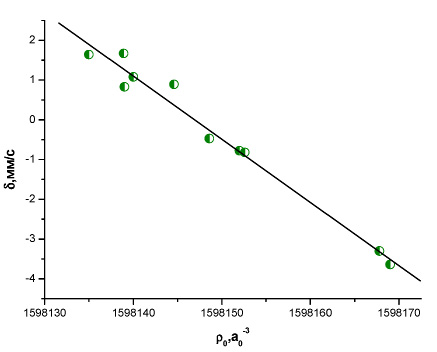
Рис. 8. Зависимость между экспериментальным изомерным сдвигом и рассчитанной методом BP86/TZ2P+ электронной плотностью на ядре 187Os
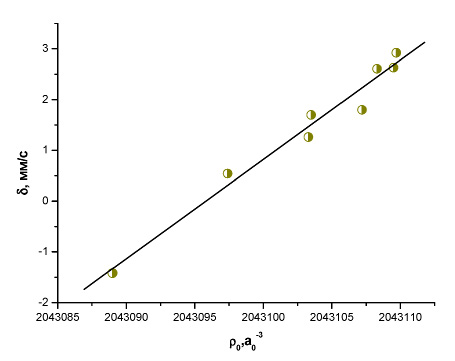
Рис. 9. Зависимость между экспериментальным изомерным сдвигом и рассчитанной методом BP86/TZ2P+ электронной плотностью на ядре 197Au (I)
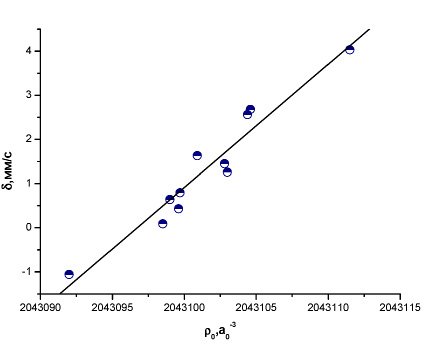
Рис. 10 Зависимость между экспериментальным изомерным сдвигом и рассчитанной методом BP86/TZ2P+ электронной плотностью на ядре 197Au (III)
Кроме того, были получены линейные корреляции между Мёссбауэровскими и рентгеновскими фотоэлектронными сдвигами для некоторых соединений. Из полученных линейных корреляций между Мёссбауэровскими и фотоэлектронными сдвигами для SbCl5L комплексов [15] (рис. 11, 12) следует, что заселенность 5s-орбитали атома сурьмы близка во всех комплексах, а изменения в мёссбауэровском химическом сдвиге вызываются также экранированием 5р-электронами атома сурьмы. Аналогичные зависимости наблюдались для других атомов, в частности, смешанных ионных комплексов
олова [2].
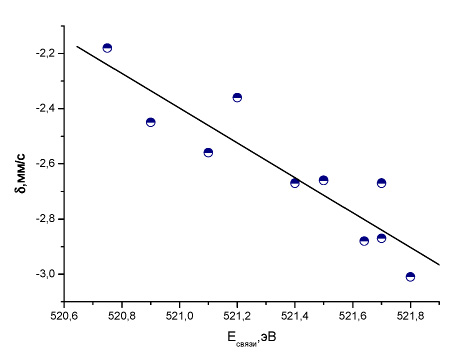
Рис. 11. Зависимость между экспериментальным изомерным сдвигом и рассчитанной методом BP86/TZ2P+ энергией связи в SbCl5L комплексах
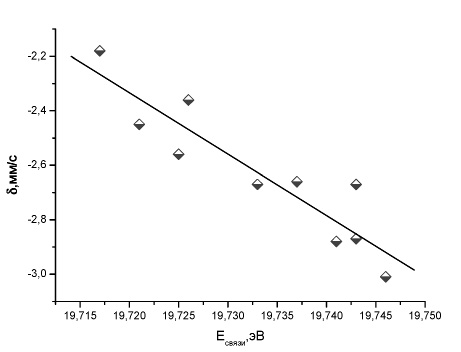
Рис. 12. Зависимость между экспериментальным изомерным сдвигом и рассчитанной методом B3LYP/DGDZVP энергией связи в SbCl5L комплексах
Ранее были предложены молекулярные модели для различных мёссбауэровских ядер, которые дают простые аналитические выражения заселенности s-, p- и d- электронов в зависимости от симметрии, типа лиганда, и межатомного расстояния металл-лиганд [1]. Эти модели обеспечивают достаточно простую интерпретацию изменений в значениях δ для различных серий металлических соединений. Для различных мёссбауэровских атомов были найдены очень хорошие корреляции между изомерными сдвигами и орбитальными заселенностями [16, 17]. Для соединения йода основной вклад в изомерный сдвиг происходит от заселенности 5s-орбитали, для олова и сурьмы значительный вклад также дает экранирование 5р-орбиталями:
для соединений йода:
d = –290 Ns + 13 Np + 95Ns2 –8NsNp +
+ 224 (r=0.977; s=0.1; n=9), (1)
для соединений сурьмы:
d = 5.6 Ns –2.1Np – 10.9Ns2 +1.3NsNp +
+1.3 (r=0.996; s=0.5; n=16), (2)
для соединений олова:
d = 12.5 Ns –26.4Np – –32.1Ns2 +28.4NsNp +
+ 17.4 (r=0.985; s=0.05; n=17). (3)
На основе наших теоретических результатов с использованием B3LYP/LanL2DZ метода расчета для соединений Au (I) и Au (III) получены следующие корреляции:
для соединений Au(I):
d = –6 + 16 Ns – 1 Nd (r=0.94;
s=0.4; n=10), (4)
для соединений Au(III):
d = –11 + 2 Ns – 1 Nd
(r=0.99; s=0.1; n=7). (5)
Эти зависимости включают как прямой эффект влияния 6s-электронов, так и экранирование ядра d-электронами. В соответствии с уравнением (4), можно видеть значительно больший вклад 6s-орбитали, чем 5d-орбитали атома золота в его изомерный сдвиг.
Если в соединениях Au (I), химическое связывание определяется в основном s- и в меньшей степени d-орбиталями центрального атома, то в соединениях Au (III) вклад d-орбиталей значительно увеличивается (5), что объясняется увеличением числа связей атома золота.
Подобные результаты получены нами при расчете методом B3LYP/LanL2DZ соединений платины:
для соединений Pt(II):
d = 0.4 – 2.6 Ns + 0.2 Nd
(r=0.96; s=0.1; n=5), (6)
для соединений Pt(IV):
d = –7.1 – 0.6 Ns + 0.9 Nd
(r=0.98; s=0.1; n=5). (7)
В соединениях Pt (IV), экранирование ядра 5d-орбиталями дает больший вклад в изомерный сдвиг (7). Различные знаки коэффициентов при Nd для соединений золота и платины согласуются с различными знаками dR/R (изменение радиуса ядра) для этих ядер. Различные наклоны зависимостей между электронной плотностью на ядре и Мёссбауэровским сдвигом для разных мёссбауэровских ядер также определяются различными знаками при dR/R.



