Постановка задачи
Рассмотрим стационарное уравнение Шрёдингера с двумя независимыми переменными, которое формально, отвлекаясь от физического смысла аргументов, можно записать в следующем виде [3]
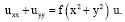
В частных случаях при
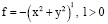
для последнего уравнения найдены корректные постановки краевых задач в определённых условиях [4–5].
В представленной работе исследуется Задача. В области
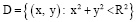
найти решение уравнения
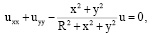(1)
удовлетворяющее граничному условию
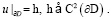(2)
Замечание 1. В дальнейшем для упрощения выкладок будем считать радиус круга единицей масштаба рассматриваемой системы координат: R=1.
Разделение переменных по методу Фурье
Нетривиальное решение граничной задачи 1 будем искать в полярных координатах в виде
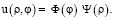(3)
В результате подстановки произведения (3) в уравнение (1) и разделения переменных с постоянной λ получается уравнение для функции
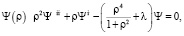(4)
и задача на собственные значения для функции
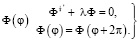(5)
Общее решение однородного линейного уравнения (5) определяется с помощью характеристического уравнения в виде суперпозиции гармоник
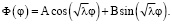
Для того, чтобы Ф была однозначной периодической функцией, должно выполняться
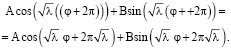
Выбирая собственные значения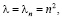 
получаем
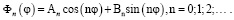(6)
При каждом фиксированном n из (4) получаем
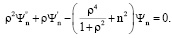. (7)
Так как уравнение (7) при любом заданном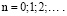 
имеет особую точку при 
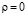, его решение будет иметь вид степенного ряда, начинающегося с 
:
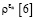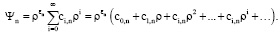(8)
Значения характеристического показателя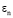 
и коэффициентов 
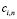можно определить подстановкой ряда (8) в уравнение (7). Последовательно приравнивая к нулю коэффициенты при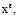 
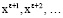получаем систему следующих уравнений
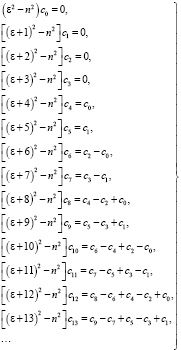
Считая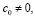 
из первого уравнения находим 
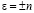. Чтобы найти сингулярное ограниченное при 
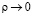решение уравнения (7), полагаем 
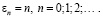Тогда из последней системы заключаем, что 
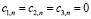. В этом случае все последующие нечётные коэффициенты 
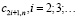также должны быть равны нулю, а все чётные коэффициенты определятся через сумму предыдущих по альтернативным формулам
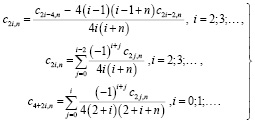(9)
Последовательное применение формулы (9) при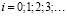 
позволяет получить выражение
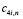через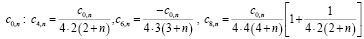 
,
,
. . .
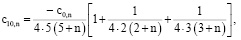
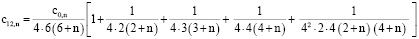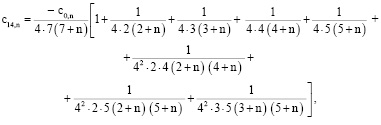
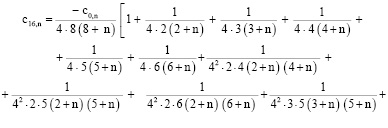
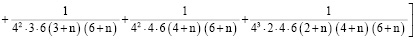
При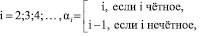 
или
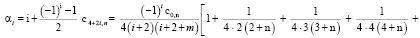
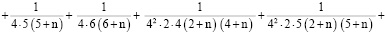
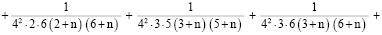
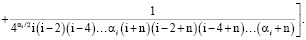(10)
Обозначим специальные вспомогательные функции
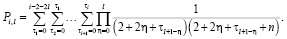(11)
Полагая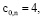 
уравнения системы (10) при 
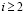можно записать в виде
, 
,
. . .
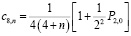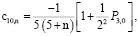
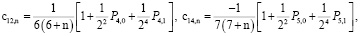
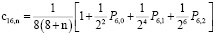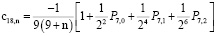
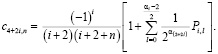(12)
Пример вычисления коэффициентов ряда (8).
По формулам (11) – (12) найти коэффициенты ряда (8): а)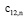 
и в)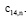 
Решение. а)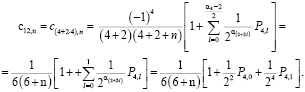 
Найдём значение коэффициента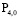 
:
.
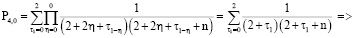
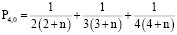Определим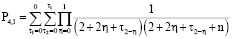 
.
Так как
,
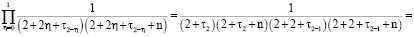
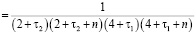имеем
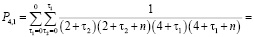
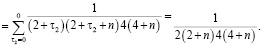
Подставляя 
и 
в формулу
,
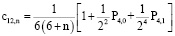получим
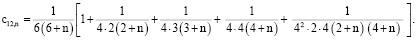
в)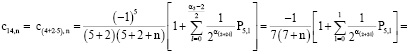 
.
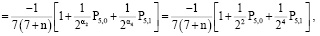
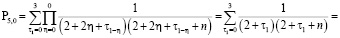
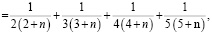
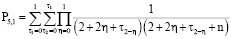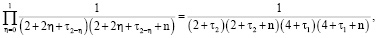
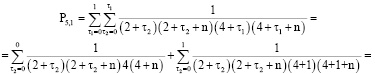
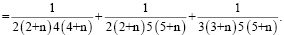
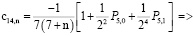
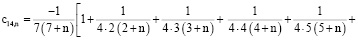
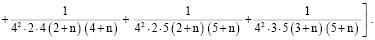
Алгоритм вычисления коэффициентов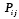 
Для простоты алгоритм вычисления коэффициентов ряда
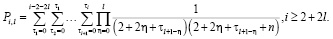
рассмотрим на примере составления кратных сумм вида
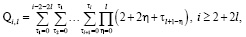
Определим сначала последовательности сумм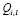 
c одинаковым индексом 
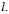При 
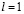получаем
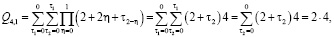
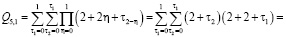
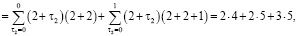
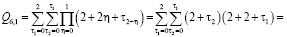
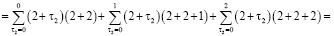
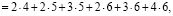
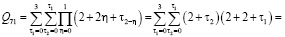
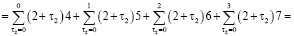
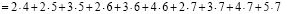и т.д.
Последовательности множителей в слагаемых рассмотренных сумм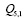 
, 
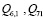можно легко составить с помощью треугольных матриц
, 
, 
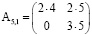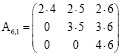Так как этим свойством обладают все выражения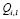 
, назовём их кратными многочленами треугольного вида, а функции 
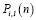, представляющие их модификацию соответственно кратными суммами треугольного вида.
Решение краевой задачи 1. Объединяя полученные результаты, определим решение задачи (1) – (2) в полярных координатах
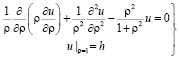(13)
по формуле (3):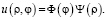 
Выше было доказано, что после разделения переменных задачи (13) получаем два уравнения, первое из которых 
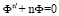имеет частные решения (6)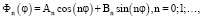 
При каждом фиксированном n второе уравнение
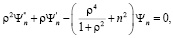
имеет частные решения вида (8)
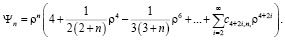
Коэффициенты степенного ряда (8) определяются по формулам (12)
, 
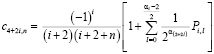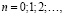
в которых
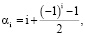
а кратные многочлены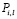 
заданы соотношениями (11)
.
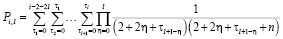Подставляя выражения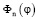 
и 
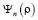в формулу (3), определяем две системы собственных функци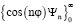й 
и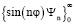 
, которым соответствуют частные решения первого уравнения (13)
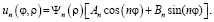
Суперпозиция всех этих решений
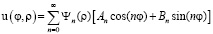(14)
также будет решением этого уравнения. Коэффициенты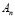 
и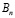 
определяются из граничного условия (13)
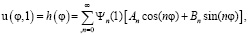(15)
если функцию 
разложить в абсолютно и равномерно сходящийся тригонометрический ряд Фурье
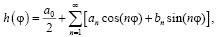(16)
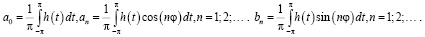
Сравнивая ряды (15) и (16), получаем
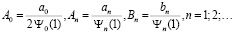(17)
Применимость принципа суперпозиции
Сходимость построенных рядов, возможность их дифференцирования в круге 
, а также непрерывность функции 
на границе этого круга доказываются классическими методами [2, с. 308–310].
С помощью альтернирующего метода Шварца построенное решение может быть продолжено за пределы круга в области более общего вида [1].