Постановка задачи при ударных упругих волновых воздействиях
В настоящее время обеспечение безопасности уникальных объектов является приоритетной задачей фундаментальной и прикладной науки.
В работах приведена информация о постановке волновых задач механики деформируемого твердого тела [1–10].
Для решения задачи о моделировании упругих волн в деформируемых областях сложной формы рассмотрим некоторое тело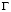 
в прямоугольной декартовой системе координат 
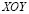, которому в начальный момент времени 
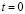сообщается механическое воздействие. Предположим, что тело 
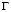изготовлено из однородного изотропного материала, подчиняющегося упругому закону Гука при малых упругих деформациях.
Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости имеют вид
, 
,
,
,
,
;
, 
,
, 
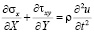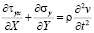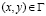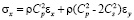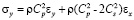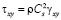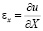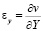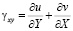, (1)
где 
, 
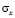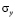и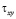 
– компоненты тензора упругих напряжени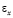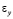й; 
, 
и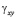 
– компоненты тензора упругих деформаци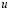й; 
и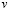 
– составляющие вектора упругих перемещений вдоль осе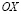й 
и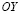 
соответственно; 
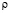– плотность материала; 
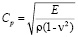– скорость продольной упругой волны; 
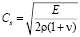– скорость поперечной упругой волны; 
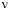– коэффициент Пуассона; E – модуль упругости; 
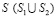– граничный контур тела Г.
Систему (1) в области, занимаемой телом Г, следует интегрировать при начальных и граничных условиях.
Разработка методики и алгоритма
Для решения двумерной нестационарной динамической задачи математической теории упругости с начальными и граничными условиями (1) используем метод конечных элементов в перемещениях.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Г, записываем приближенное значение уравнения движения в теории упругости
, 
,
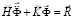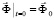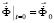, (2)
где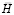 
– диагональная матрица инерции; 
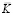– матрица жесткости; 
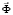– вектор узловых упругих перемещений; 
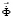– вектор узловых упругих скоростей перемещений; 
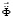– вектор узловых упругих ускорений; 
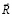– вектор внешних узловых упругих сил.
Интегрируя уравнение (2) конечноэлементным вариантом метода Галеркина, получим явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
,
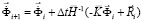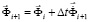. (3)
Шаг по временной переменной координате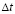 
выбирается из следующего соотношения
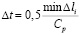
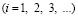, (4)
где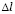 
– длина стороны конечного элемента.
На основе метода конечных элементов в перемещениях разработана методика, разработан алгоритм и составлен комплекс программ для решения двумерных линейных и нелинейных задач при различных начальных и граничных условиях, для областей сложной формы. Комплексы программ написаны на алгоритмическом языке Фортран-90.
В работах приведена информация о достоверности численного моделирования нестационарных волн напряжений в областях различной формы [4–6, 8–10].
Определение контурных напряжений в защитной оболочке реакторного отделения атомной станции
Рассматривается задача об ударе самолета (рис. 2) на систему сооружение-фундамент – основание (Архангельская атомная станция) при воздействии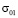 
(
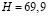м) (рис. 1).
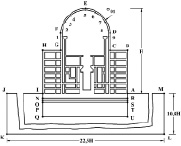
Рис. 1. Постановка задачи для Архангельской атомной станции
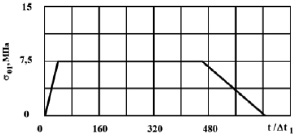
Рис. 2. Воздействие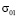 
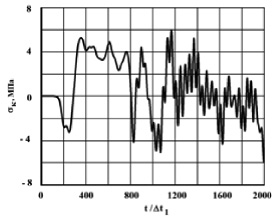
Рис. 3. Изменение упругого контурного напряжения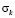 
в точке 1 во времени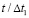 
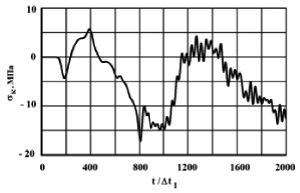
Рис. 4. Изменение упругого контурного напряжения 
в точке 2 во времени 
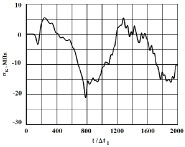
Рис. 5. Изменение упругого контурного напряжения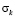 
в точке 3 во времени 
Рис. 6. Изменение упругого контурного напряжения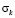 
в точке 4 во времени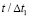 
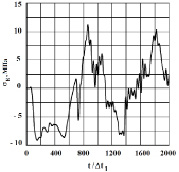
Рис. 7. Изменение упругого контурного напряжения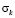 
в точке 5 во времени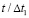 
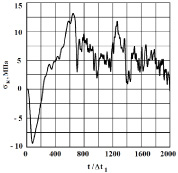
Рис. 8. Изменение упругого контурного напряжения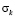 
в точке 6 во времени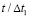 
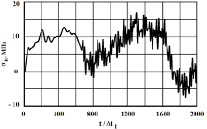
Рис. 9. Изменение упругого контурного напряжения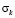 
в точке 7 во времени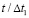 
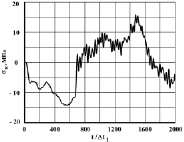
Рис. 10. Изменение упругого контурного напряжения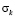 
в точке 8 во времени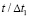 
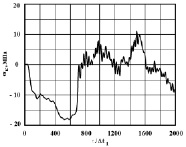
Рис. 11. Изменение упругого контурного напряжения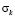 
в точке 9 во времени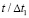 
Начальные условия приняты нулевым. Граничные условия для контура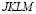 
(рис. 1) при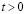 
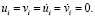Отраженные волны от контура 
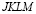не доходят до исследуемых точек при 
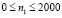. На границах материалов с разными физическими свойствами приняты условия непрерывности перемещени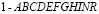й (
и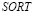 
; 
; 
; 
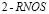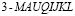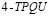). Исследуемая расчетная область имеет 
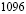узловых точек. Получены контурные напряжения в защитной оболочке реакторного отделения атомной станции.
В работах [1–2, 7] приведена информация о моделировании нестационарных волн напряжений в защитной оболочке реакторного отделения атомной станции при ударных воздействиях.
Получены контурные напряжения в защитной оболочке реакторного отделения атомной станции. На рис. 3–11 показано изменение контурных напряжений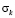 
в защитной оболочке во времени 
.
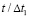Вывод
Полученные результаты позволяют оценить несущую способность защитной оболочки реакторной отделения атомной станции при ударе самолета.