Среди специфических для математики способов познания и приемов мышления помимо общих (анализ и синтез; логическое упорядочение данных и др.) в составе математической культуры имеет смысл особо выделить моделирование, метод аналогий, коды записи и переработки информации. К ним относятся: образный (воображение), словесный и словесно-символический, изобразительный и предметный (материализация, эксперимент, овеществление) и действенный (перевод информации в физические или умственные действия) [3]. Овладению кодами и переходами между ними можно и нужно обучать уже на материале школьных учебных дисциплин, тем более они должны быть включены в УМиЗ для самостоятельной работы.
Существенные условия успешного протекания познания определяются наличием или постепенным возникновением у человека [2, 8]:
а) познавательного отношения к ситуации, объекту или соучастнику познания, б) мотива разрешения ситуации – задача «для меня», в) личностного смысла знаний и г) личного опыта построения и использования знаний (совокупности математических задач, понятий, утверждений, алгоритмов и т.п.) как средств понимания и познания. Эти условия необходимо и можно создавать в процессе обучения, руководствуясь общей структурной схемой акта познания [3, с. 196] (приведём здесь отдельные шаги):
- студенту необходимо попасть в ситуацию выбора, если человек делает попытку разрешить ситуацию собственными усилиями (хотя бы и с помощью Другого), то он принимает задачу и формулирует ее в форме «для себя». Тогда в действие включаются его «естественные способности», «родовые силы» (Фома Аквинский, К. Маркс): способность и воля из-обретать (М.М. Бахтин), экстериоризировать (Л.С. Выготский) новое идеальное средство – образ, задачу, действие и т.п. Это уже знание в действии;
- совокупность изобретенных средств-знаний применяется для мысленного или практического разрешения ситуации; накапливается опыт в виде совокупности действий, видов и «программ» деятельности с использованием полученных знаний в их сочетании с ранее уже известными;
- появляется необходимость осмысления средств с помощью различных культурных знаков: ряда «умственных» образов, их словесно-символического описания и преобразования, материализации в динамических рисунках, схемах, алгоритмах, новых задачах, в другом материале;
- средства и совокупность действий с ними испытываются на допустимость применения и «прочность», теоретическую или прикладную, усиливая личную ответственность человека за найденные или изобретенные средства, за свои действия и полученные результаты;
- осуществляется поиск продуктивной организации обретённых знаний (в том числе методов), что нередко приводит к формированию объединяющих, по-новому организующих деятельность «мета-знаний» [1, 8], становящихся своеобразными «ступеньками», составляющими ядро знаний;
- в случае успеха в достижении цели (как предполагаемого результата) с новым средством и результатами опыта знакомят других участников, т.е. осуществляется коммуникация, в том числе – для своеобразного «шлифования» найденных средств и уточнения пути разрешения ситуации;
- приобретенный опыт ретроспективно осмысливается, рефлектируется. Результаты сравнивают с запланированными, средства и способы решения анализируют и корректируют. Осуществляется презентация продукта – еще один способ усиления личной ответственности;
- наконец, ставятся новые задачи для других ситуаций, исследование входит в новую фазу возможного переноса на новые ситуации и задачи…
Намеченной структурной схеме завершенного акта учебного познания можно придать наглядную форму, что и зафиксировано в «Обобщенной модели научного познания» [3, с. 196]. Она как раз и используется нами в качестве основного ориентира при создании УМиЗ по организации познавательной деятельности студентов физико-математического факультета. В них студентам предлагается овладевать уже упоминавшимися культурными знаками, в том числе и в логике известного наглядного моделирования [6], в некоторых важных моментах совпадающего с логикой акта научного познания, детально разработанной с позиций мировоззренческого подхода [3].
Приведём, наконец, примеры созданных нами комплексов материалов и заданий, выстроенных в частичном соответствии с обозначенной теоретической основой – системой принципов. В них также учитывается порядок ознакомления первокурсников с программным учебным материалом по курсу математического анализа (введение).
Пример 1. Фрагмент лекции (культурно-исторический экскурс): «Известный математик Норберт Винер разграничивал математические дисциплины по уровню абстракции их основных объектов. К 1-му уровню он относил арифметику, связанную с понятием «индивидуального числа» и его свойствами, но не использующую символы для любого числа (как, например, в школьном курсе алгебры). На 2-й уровень – алгебру, которая изучает уже индивидуальные комбинации (мы говорим: действия или операции, а также отношения равенства и неравенства) чисел вообще и свойства таких комбинаций. 3-й уровень абстракции Винер связывал с функциями, т.е. с произвольными зависимостями между числами или группами чисел. Именно на этом уровне рассматриваются функции натурального (из N) и действительного (из R) аргумента, индивидуальные функции (показательная, логарифмическая) в их различных комбинациях (арифметические действия; сложные и обратные функции), появляются представления о различных видах (классах) функций, в том числе элементарных. А именно: линейные, квадратичные, целые, дробно-рациональные, иррациональные, тригонометрические и др. С большей или меньшей подробностью они, их свойства и графики изучались в школе в курсе алгебры и начал анализа.
Наконец, Винер выделяет еще и 4-й уровень абстракции, предметом рассмотрения на этом уровне являются уже различные преобразования самих функций и даже их классов, причем заданных на множествах, отличающихся от множества R. Такие преобразования переводят функцию в другую функцию, в математике их называют операторами. К числу простейших из них относят дифференцирование и интегрирование функций одной и нескольких переменных, функций комплексного переменного и т.п. Функции, классы функций, операторы и связанные с ними другие объекты составляют предмет изучения математического анализа, а основной метод изучения этих объектов – метод бесконечно малых или, что то же самое, метод пределов. В чем заключается этот метод, как его использовать – нам и предстоит понять».
Вопросы-задания. 1. Что вам известно о Норберте Винере? Занимался ли он вопросами математического анализа? 2. Найдите сведения о нём в энциклопедиях: годы жизни, учёбы, учёные степени и звания, основные увлечения, открытия в математике. 3. Прочитайте найденные, заинтересовавшие вас фрагменты текстов вслух и послушайте себя: что заинтересовало, подслушайте свои мысли, запишите их, как если бы вы рассказывали их кому-то? 4. С какими новыми терминами вы встретились в этой лекции, что они означают? Зафиксируйте их значения в тетрадях для самостоятельной работы (в дальнейшем тс/р). 5. Как вы понимаете слово абстракция? Приведите в тс/р примеры абстракций каждого уровня, выделенного Н. Винером. Что у вас не получилось? Какие вопросы, недоумения возникли, попробуйте ответить – почему? 5. Почему, на ваш взгляд, ни в одном из уровней абстракции Н. Винером не названа геометрия? Выскажите своё мнение.
Пример 2. Фрагмент лекции-беседы «Основные и обратные арифметические операции в терминах, символах, свойствах». Сводная таблица.
Мы продолжаем изучать начала математического анализа числовых функций, и нам не обойтись без знаний свойств самих чисел и – главное – действий с ними. Всё это вы изучали в школе, начиная с 1-го класса, наши задачи сейчас – 1) понять, на каком уровне – по Н.Винеру (см. 1-я лекция) – вы всё это изучали и поняли и 2) поднять наши знания на более высокий уровень. Запишите эти задачи, что у вас получилось? Как вы их поняли?
Итак, какие основные операции во множестве чисел (говорят: над числами) вы знаете, назовите их. (Как правило, студенты перечисляют всё подряд: +, –, ´ и т.д., не отличая основные и производные, прямые и обратные операции, не вспоминая даже возведение в натуральную степень, изредка называют «извлечь корень» – таковы, к сожалению, факты).
Назовите эти операции по имени, то есть назовите термины. Какие из этих операций непосредственно связаны друг с другом, как? Связаны ли непосредственно, например, сложение и возведение в степень, вычитание и сложение и другие? (В результате группируются пары: сложение – вычитание, умножение – деление). Как символически записать эти операции и их результаты, как называются их компоненты? А можно ли говорить об операциях во множестве геометрических фигур? Знаете ли вы такие?
Итак, мы выяснили, что некоторые операции над числами образуют своеобразные пары, а в качестве основных (прямых) операций следует всё-таки признать сложение, умножение и возведение в степень. Для первых двух из них парными являются вычитание и деление. Их называют обратными для первых из приведённых. Начнём составлять таблицу, которую так и назовём «Основные и обратные арифметические операции».
Что нам необходимо использовать для краткой записи операций? Возникает необходимость использовать два рода символов: самих действий и их компонентов. Вспоминаем названия компонентов действий и их результатов, а также некоторые свойства. Как называются компоненты этих действий? Обращаем внимание на термины слагаемые, сомножители, то есть они как бы «равноправны» уже по своему названию, а по смыслу? На данном этапе важным из свойств является коммутативность (переместительность) сложения и умножения. Но не так дело обстоит с возведением в степень; эта операция не коммутативна: 23 ¹ 32. Желательно по ходу беседы напомнить о названиях: действия 1-й, 2-й и 3-й ступеней, и о правилах скобок. Постепенно заполняется первая строка таблицы:
|
Прямое действие (операция) (I) |
Сложение a + b = b + а = c (II) |
Умножение a · b = b · a = c (III) |
Возведение а в b-ю степень ab = c. Для этой операции можно использовать и такой символ: а↑ b = с. (IV, V) |
Дальнейшее заполнение таблицы идёт сверху вниз, слева направо и сопровождается подчёркиванием различия между действиями первой, второй и третьей ступени. Важные задачи: а) продолжить формирование исследовательских умений (вопросы, поиск ответов и т.д.); б) начать интегрировать знания об основных арифметических операциях; акцентировать внимание на сходстве и различии в появлении обратных операций (для возведения в степень необходимы две обратных операции); в) начать исследование вопроса необходимости перехода к понятию функции.

Дальнейшее заполнение таблицы идёт сверху вниз
Проанализируем, как появляются новые (впрочем, частично нам известные) операции и новые понятия на базе основных (прямых) операций… Добиваемся понимания: вычесть (разделить) – значит найти такое неизвестное число х, которое при сложении с известным (умножении на известное) даёт нам результат основного действия. Как называются эти новые (относительно основных) операции? Нам потребовалось и новое (относительно) понятие.
Подметим, что это понятие относится к результату новой (обратной) операции. Так часто поступают и в обыденной жизни: новому неизвестному мы даём новое название, чтобы как-то отличить его от знакомых объектов. Приведите свои примеры! Заметим, что в первой и второй колонках по два уравнения, но для обоих – одно обратное действие и одно понятие. Как вы думаете, почему это оказалось возможным – единственное обратное действие? Как это связано со свойствами прямых действий? И т.д.
Исторический экскурс: Какова этимология слов: «корень» («радикал»), «логарифм»? Внимательнее вдумаемся в последнее слово-термин? Кем и когда, для каких целей использовался? Почитаем внимательно, например, учебник и вначале устно, а затем в тс/р ответим на вопросы: 1. Слово «логарифм» произошло от соединения двух греческих слов: λογος – отношение, άριθμοζ – число. Ввёл его шотландский барон Джон Непер (1550 – 1617). Он исходил при этом из идеи функциональной зависимости, представленной в виде двух шкал (см. рисунок). Что, по вашему мнению, изображено на этих шкалах? Одинаковые ли по длине отрезки на одной и той же шкале, почему? что бы это значило? на этих шкалах в их сравнении [Мк, Мк+1] и [mк, mк+1], почему?
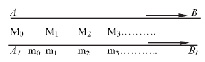
2. Чем ещё в математике известны имена Дж. Непера, Симона Стевина, И. Кеплера? Как их работы были связаны с анализом бесконечно малых, друг с другом и с идеей функциональной зависимости? Как удачно найденное слово превратилось в научный термин? Задание: напишите в тс/р обо всём вами понятом небольшую работу. Вернёмся к таблице и сделаем выводы…
Далее, опираясь на последнюю строку таблицы, постараемся понять: зачем и как появляется необходимость в таком фундаментальном понятии математики как функция…
Выскажите свою точку зрения, ваше понимание вопроса…



