Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Цели обучения в современных федеральных государственных образовательных стандартах сформулированы в терминах компетенций, формируемых у студентов в результате изучения той или иной дисциплины и всего образовательного цикла. Переход на компетентностно-ориентированное образование заключается в требованиях формировать в результате обучения как профессиональные, так и общекультурные компетенции, значимые не только в будущей профессиональной деятельности, но и в общесоциальной адаптации. Удобным средством достижения результативности в формировании общекультурных и профессиональных компетенций являются компетентностные задачи.

Болотов В.А. определяет компетентностно-ориентированное задание как задание, которое требует использования знаний за пределами учебной ситуации, организует деятельность учащегося, а не требует воспроизведения им информации или отдельных действий [1].

Теория вероятностей как учебная дисциплина является одним из базовых курсов в системе высшего экономического образования, так как практически все экономические показатели являются по своей сути случайными величинами и их реализация должна рассматриваться в условиях риска и неопределенности [2].

Большинство учебных пособий по теории вероятностей, опубликованных в нашей стране, содержат мало компетентностных задач, либо эти примеры имеют однобокую (например, военную) тематику. Однако, для эффективного использования на практике полученных теоретических знаний студент должен уметь самостоятельно строить математические модели для конкретных прикладных задач.

Таким образом, анализ литературных источников по проблеме исследования позволяет сделать вывод о том, что компетентностные задачи обладают богатейшим потенциалом для формирования некоторых компетенций, необходимых каждому специалисту, однако проблема их включения в процесс обучения теории вероятностей разработана недостаточно.

Резюмируя вышесказанное, можно сделать вывод о том, что в процессе обучения студентов теории вероятностей в настоящее время имеется следующее противоречие: между существующими потенциальными возможностями компетентностных задач в формировании общекультурных и профессиональных компетенций студентов и недостаточной разработанностью технологии их включения в процесс обучения теории вероятностей. Сформулированное противоречие определяет цель исследования, которая состоит в разработке научно обоснованных методических рекомендаций по обучению студентов теории вероятностей. В основу исследования положена гипотеза о том, что включение компетентностных задач в процесс обучения теории вероятностей является необходимым условием успешного формирования общекультурных и профессиональных компетенций, отраженных в требованиях высшего профессионального образования.

Для проверки выдвинутой гипотезы использовался комплекс взаимодополняющих методов: теоретический анализ философской, психолого-педагогической, методической и исторической литературы по теме исследования, государственных стандартов высшего профессионального образования, учебных пособий; педагогический эксперимент по апробации и коррекции разработанной методики, в ходе которого использовались педагогическое наблюдение, беседы с преподавателями и студентами, проводились лекции, практические занятия по дисциплине «Теория вероятностей и математическая статистика».

Теоретические аспекты применения компетентностных задач

Под компетентностными задачами, рассматриваемыми при изучении математики, понимают задачи, целью решения которых является разрешение стандартной или нестандартной ситуации (предметной, межпредметной, практической) посредством нахождения соответствующего способа с обязательным использованием предметных (математических) знаний [8].

Харитонова О.В. и Павлова Л.В. выделяют следующие виды компетентностных задач: предметные, межпредметные и практические [8]. Для краткости приведем их в табл. 1.

Материалы и методы исследования

Приведем несколько примеров компетентностных задач в процессе изучения теории вероятностей.

Предметные компетентностные задачи.

Задача 1. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг:

а) квадрата;

б) правильного треугольника.

Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга [4].

Задача 2. Ребро куба х измерено приближенно, причем а ≤ х ≤ b. Рассматривая ребро куба как случайную величину X, распределенную равномерно в интервале (a, b) найти математическое ожидание и дисперсию объема куба [4].

Данные задачи соответствует следующим характеристическим особенностям компетентностной задачи: условие задачи сформулировано как математическая ситуация, для разрешения которой используются знания, на которые нет явного указания в тексте задачи (формулы площадей и объемов из геометрии, вычисление интегралов из математического анализа); эти задачи могут быть использованы при решении других задач. Следовательно, в результате работы с такими задачами студент будет владеть культурой мышления и способностью к обобщению, анализу, восприятию информации.

Таблица 1

Виды компетентностных задач

Межпредметные компетентностные задачи.

Задача 3. В момент закрытия биржи значение индекса активности было равно 9246 пунктам. На следующий день ожидается подъем в среднем на 4 пункта со средним квадратичным отклонением 115 пунктов. Предполагая, что величина индекса имеет нормальное распределение, найдите вероятность того, что на следующий день будет наблюдаться:

а) снижение индекса активности;

б) повышение индекса активности более чем на 50 пунктов;

в) повышение индекса активности более чем на 100 пунктов;

г) снижение индекса активности более чем на 150 пунктов;

д) колебание, превышающее 200 пунктов в любую сторону. [3]

Подобные задачи способствуют развитию исследовательских умений: анализа (выявления проблем, сбора информации), обобщения. Условие задачи сформулировано как экономическая ситуация, для разрешения которой используются знания из экономики. В результате работы с такими задачами студент способен понимать и анализировать экономические проблемы; осознает социальную значимость своей будущей профессии, обладает высокой мотивацией к выполнению профессиональной деятельности; способен осуществлять сбор, анализ и обработку данных, необходимых для решения поставленных экономических задач.

Практические компетентностные задачи.

Практическая компетентностная задача может стать темой для проектной работы. Основой для таких задач могут служить самые разнообразные источники: текст и вопросы из учебника, дополнительная литература, научно-популярные статьи, история математики, проблемы реальной жизни и т.п. Приведем две темы проектно-исследовательских работ с использованием компетентностных задач по теории вероятностей.

Метод проектов предполагает решение какой-то проблемы, противоречия, парадокса. История развития теории вероятностей полна интересных парадоксов. В качестве тем проектов можно предложить студентам парадоксы теории вероятностей, различные попытки их решения, установление связей парадокса с окружающей действительностью, его влияния на развитие наук и их приложений [5].

Задача 4. Санкт-Петербургский парадокс и его значение для экономической теории. Единичное испытание в петербургской игре состоит в бросании правильной монеты до тех пор, пока не выпадет решка; если это произойдет при n-м бросании, игрок получает 2n долларов из банка. Таким образом, с каждым бросанием выигрыш удваивается. Вопрос в следующем: сколько следует заплатить игроку за участие в игре, чтобы игра стала безобидной? Безобидность петербургской игры рассматривается в классическом смысле: среднее значение (или математическое ожидание) чистого выигрыша должно быть равно 0. Однако, как ни удивительно, это естественное требование невыполнимо, какую бы (конечную) сумму денег игрок ни заплатил [9].

В качестве связи парадокса с другими науками можно предложить студентам разобраться в связи между данным парадоксом и теорией ожидаемой полезности.

При выборе темы для проектов соблюдается главный педагогический принцип: как можно полнее учесть интересы студентов, как можно ближе подойти к волнующим их проблемам, подобрать сложную, но посильную им задачу, способствующую развитию. Поэтому студентам нужно предложить разные темы для проектных работ.

Задача 5. Предполагается открыть новое кафе в черте города. Проанализируйте два района города, выясните:

1) шансы получить место для него в одном из двух районов;

2) шансы успеха проекта.

Как можно оценить те и другие шансы? Составьте соответствующий бизнес-план проекта.

Метод проектов предполагает самостоятельное приобретение недостающих знаний из разных источников, развитие умений пользоваться этими знаниями для решения новых познавательных и практических задач, развитие способности применять знания к жизненным ситуациям. Подобные задачи способствуют формированию компетенции принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность. Работа над проектом позволит студентам организовывать собственную деятельность, выбирать типовые методы и способы выполнения задач, оценивать их эффективность и качество, самостоятельно определять задачи личностного развития, заниматься самообразованием. Работая над проектом в малых группах, студенты учатся работать в коллективе и в команде, а это в свою очередь создает условия для формирования умений продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции коллег, эффективно разрешать конфликты, брать на себя ответственность за работу членов команды [6].

Результаты исследования и их обсуждение

Разработанные методические рекомендации прошли опытную проверку. Опытно-экспериментальной базой исследования были две группы: контрольная (группа 1) и экспериментальная (группа 2) студентов второго курса, обучающихся по специальности «Экономика» (080100) в институте экономики и предпринимательства Нижегородского государственного университета.

На начальном этапе обучающего эксперимента изучалось состояние математической подготовки студентов выбранных групп. Была проведена контрольная работа по дисциплине «Элементы высшей математики». В экспериментальной группе занятия по теории вероятностей были организованы по специальной методике, которая включает в себя компетентностные задачи трех видов: предметные, межпредметные и практические. По окончании изучения дисциплины была проведена контрольная работа по теории вероятностей как в экспериментальной, так и в контрольной группах. Данные количественного анализа контрольных работ приведены в табл. 2.

Данные (оценки) измерены в порядковой шкале. Поэтому для определения соответствия между данными контрольной и экспериментальной групп до проведения эксперимента и различий между данными контрольной и экспериментальной групп после проведения эксперимента целесообразно воспользоваться критерием однородности χ2, эмпирическое значение 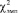которого вычисляется по формуле

.

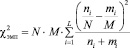N – количество человек в экспериментальной группе, M – количество человек в контрольной группе, ni – число членов экспериментальной группы, получивших i-й балл, mi – число членов контрольной группы, получивших i-й балл, L = 3 (минимальный, общий, продвинутый) [7].

Для L = 3 критическое (табличное) значение 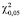= 5,99 (для уровня значимости 0,05). Посчитаем 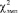до и после проведения эксперимента: если 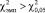, то можно сделать вывод о том, что достоверность различий характеристик сравниваемых выборок составляет 95 %; если 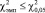, то можно сделать вывод о том, что характеристики сравниваемых выборок совпадают с уровнем значимости 0,05. Эмпирические значения критерия χ2 для полученных данных приведены в табл. 3.

Выводы

Итак, можно сделать следующие выводы:

1) характеристики всех сравниваемых выборок, кроме экспериментальной и контрольной групп, после окончания эксперимента, совпадают с уровнем значимости 0,05. Значит, выбранные группы равноценны по уровню математической подготовки.

2) так как 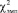= 6,02, а 6,02 > 5,99, то достоверность различий характеристик экспериментальной и контрольной групп после окончания эксперимента составляет 95 %.

Начальные (до начала эксперимента) состояния экспериментальной и контрольной групп совпадают, а конечные (после проведения эксперимента) – различаются. Следовательно, можно сделать вывод, что эффект изменений обусловлен именно применением экспериментальной методики обучения. А значит, выдвинутая гипотеза о том, что если обучение студентов теории вероятностей и математической статистике реализовать на основе использования специальной методики, которая включает в себя компетентностные задачи, то это будет способствовать более успешному формированию компетенций будущего специалиста, верна.

Таблица 2

Анализ контрольных работ