Циклические нагрузки, изменяющиеся по величине и напряжению, при которых работают некоторые детали машин и конструкций, заметно снижают прочность и долговечность, так как при повторно-переменном напряжении металл разрушается от усталости. Характерной особенностью такого разрушения является тот факт, что разрушение происходит при напряжениях меньших предела прочности, текучести и упругости. В металлах и сплавах появляются микротрещины, которые постепенно развиваются и приводят к разрушению деталей [1-13].
Известно, что на сопротивление разрушению металлов и сплавов при циклическом нагружении оказывает влияние большое количество факторов: природа металла, температура, масштабный эффект, концентрация напряжений, асимметрия циклического нагружения, частота циклов и др. [8,12,14-19].
Целью работы является изучение изменения структуры и повреждаемости поверхности стали 30ХГСН2А в процессе различных видов циклического нагружения, и определение закономерностей изменения показателей сопротивления усталости в зависимости от влияния частоты циклического нагружения и масштабного эффекта.
Неоднозначное влияние фактора ω и масштабного эффекта было рассмотрено в ряде работ [14÷20]. Изменение частоты циклических напряжений приводит к изменению скорости деформации, а при нагружении образца сначала деформируется его поверхностный слой [21-22]. Деформация поверхностного слоя именуется поверхностными эффектами. Поверхностные эффекты есть следствие физических процессов, происходящих в слое с аномальными свойствами. В представленной работе основное внимание уделено исследованию изменений микро и субмикроструктур в процессе циклического нагружения.
В настоящее время механическое оборудование работает в широком диапазоне напряжений и долговечности от области малоциклового нагружения до базового числа циклов усталости. Фиксированная величина, предел выносливости не соответствует надежной оценке сопротивления усталости деталей машин и конструкций. Чтобы указанная оценка была более надежной, должны фигурировать две величины: напряжение (ограниченный предел выносливости σ) и долговечность (количество циклов до разрушения N). Тогда следует ввести показатель, выражаемый отношением приращения напряжения dσ к приращению долговечности dN. Таким образом, получаем тангенс угла наклона касательной к кривой усталости и соответственно к оси N. Сравнение поведения разных металлов по тангенсу угла наклона, записанному в виде отношения dσ/dN является сложным, так как в каждый последующий момент описанная функция насыщается. Таким образом, обычные координаты σ – N не являются удобными. Удобными координатами являются логарифмические. Они удобны тем, что кривые усталости, в сущности, превращаются в прямые.
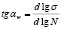
представляет собой постоянную величину, что позволяет проводить обобщения широкой гаммы материалов и условий их испытания. Наклон tg αw зависит от ряда различных факторов. Факторы, определяющие природу усталости, так или иначе влияют на положение кривой в координатах lg σ – lg N, поэтому наклон tg αw может выступать как характеристика, отображающая физические явления, происходящие в образцах (деталях), а точнее, в их поверхностных слоях, которые имеют свойства, отличные от свойств глубинных слоев материала [14÷20].
В материале этих слоев при деформации деталей происходят физические процессы повреждаемости. Проблема оценки прочности и долговечности деталей машин и конструкций по повреждению материала поверхностных слоев, в настоящее время особенно актуальна, т.к. увеличилось количество катастроф, аварий и т. п. связанных с усталостным разрушением используемых материалов.
Повреждение поверхности оценивается по изменению микроструктуры материала под действием циклических напряжений [23-27]. В качестве оценочной характеристики служат полосы скольжения, возникающие на шлифе образца, изготовленного в зоне наибольших напряжений [28-30]. Для исследований были изготовлены образцы небольшого диаметра (5 и 10 мм) и плоские (3х3 мм) с десятикратной длиной. Испытания образцов обрабатывались методом математической статистики с построением «спрямленных» кривых усталости по уравнению:
lg σ = (lg σ)0 – tg αw lg N
при удовлетворительном коэффициенте корреляции (Ккор).
Наряду с параметром сопротивления усталости tg αw, речь идет и о повреждаемости поверхности, оценочным показателем которой являются полосы скольжения [31-35]. Сталь марки 30ХГСН2А является одним из лучших материалов в смысле показателя сопротивления усталости и повреждаемости поверхности. Для этой стали в закаленном состоянии tg αw = 0,08723 при испытании плоских образцов; tg αw = 0,1299 и tg αw = 0,09257 при вращении круглых изогнутых образцов диаметром 10 мм (рис. 1). Вид испытания мало сказался на величине показателя сопротивления усталости. Отжиг тех же круглых образцов привел к небольшому ухудшению показателя tg αw и к более значительному уменьшению абсолютного значения предела усталости на базе, превышающей 106 циклов (рис. 1). Увеличение абсолютных размеров образцов приводит к ухудшению показателя сопротивления усталости (рис. 2). Микроструктуры стали после испытаний представлены на рис. 3 и 4.
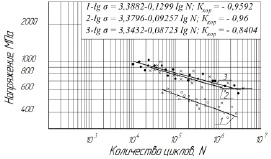
Рис. 1. Кривые усталости стали 30ХГСН2А при температуре 20̊ С: 1,2 – деформация изгиба вращающихся круглых образцов диаметром 10 мм, ω = 50 Гц (1 – образцы отожжены); 3 – деформация поперечного изгиба плоских образцов сечением 3х3 мм, ω = 3,33 Гц (закаленные образцы)

Рис. 2. Кривые усталости закаленной стали марки 30ХГСН2А при температуре 20oС: 1, 2 – образцы диаметром 5 и 10 мм соответственно
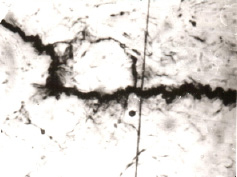
Рис. 3. Микроструктура закаленной стали 30ХГСН2А после циклического плоского изгиба образца сечением 3х3 при температуре 20oС; (х 416); ω = 3,33 Гц; σ = 930 МПа; N = 1500 циклов. Образец не разрушен

Рис. 4. Повреждение поверхности закаленной стали 30ХГСН2А после плоского изгиба образца сечением 3х3 при температуре 20oС; (х 340); ω = 3,33 Гц; σ = 980 МПа; N = 1,3·104 циклов (полная наработка). Шлиф не травлен
Выводы
У стали 30ХГСН2А выявлена закономерность соответствия показателя сопротивления усталости и повреждаемости материала поверхностных слоев образца. Соблюдается правило: чем больше повреждаемость, тем хуже сопротивляется материал усталости (больше tg αw). Зависимость tg αw = f(Ф) не прямолинейная.



