При решении задач об изгибе стержней и пластин в присутствии агрессивной окружающей среды используется выражение интегрально средней концентрация 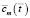агрессивной среды в объеме стержня [1, 2]:

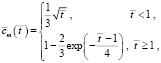
где 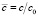, , 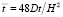Н – толщина поперечного сечения стержня, с – концентрация агрессивной среды, с0 = соnst – концентрация на поверхности стержня, D – коэффициент диффузии, t – время.

Исследуется рассеянное разрушение прямоугольной пластины при чистом изгибе в условиях нестационарного плоского напряженного состояния с учетом влияния агрессивной среды. Влияние агрессивной среды моделируется с помощью введения в определяющие и кинетические соотношения функции от интегрально средней концентрации элементов среды в материале пластины 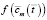. В качестве определяющих соотношений ползучести (при малых деформациях) используются или степенная, или дробно-линейная зависимости интенсивности скоростей деформаций ползучести 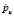от интенсивности напряжений σu.

С помощью кинетической теории Ю.Н. Работнова определяются времена до разрушения такой пластины при последовательном приложении изгибающих моментов M1 и M2 во взаимно перпендикулярных плоскостях. Время до разрушения при использовании кинетического уравнения со скалярным параметром поврежденности ωsc определяется следующим образом:

.

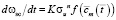Для исследования постепенного рассеянного разрушения пластины с использованием векторного параметра поврежденности ωv рассмотрим следующую систему кинетических уравнений:

,

,

,

,

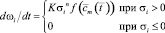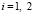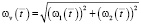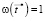ω1 и ω2 – проекции вектора поврежденности на оси 1 и 2 в плоскости пластины. В результате расчета получены времена до разрушения для различных соотношений изгибающих моментов b = M2/M1. Анализ показывает, что времена до разрушения 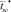и 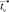удовлетворяют неравенству 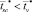при различных значениях b.

Дополнительно исследованы суммы парциальных времен S как при b > 1, так и при 0 < b ≤ 1. Показано, что эти суммы S удовлетворяют следующим неравенствам: S > 1 при M1 > M2 и 0 < S ≤ 1 при M1 ≤ M2. Проведена аналогия с результатами испытаний на длительную прочность стержней при кусочно-постоянном растягивающем напряжении.

Работа выполнена при поддержке гранта РФФИ № 14-08-00528-a.