Известно что законы сохранения энергии, импульса, момента импульса, также все три начала термодинамики имеют очень важное значение в физике и представляют большой интерес для практики. Наряду с интересом эти законы требуют досконального изучения и полного анализа, так как физические процессы этих законов связаны со многими явлениями природы.
Мы в этой статье обсудим второе начало термодинамики или по другому как его называют закон возрастания энтропии, закон который связан с тепловыми процессами в природе.
Второе начало термодинамики по формулировке Клаузиуса определяется таким образом: невозможны такие процессы, единственным конечным результатом которых был бы переход некоторого количества теплоты от тела менее нагретого к телу более нагретому.
Иными словами, теплота не может самопроизвольно переходить от холодных тел к горячим.
Все мы знаем что если тело получает извне определенную энергию, то тогда теплота может переходит от тела менее нагретого к телу более нагретому, но тогда в этом случае такой переход будет не единственным конечным результатом физического процесса.
Другая формулировка Томсона аналогична формулировке Клаузиуса, оно тоже логически вытекает из этого утверждения, на практике все мы сталкиваемся с такой ситуацией, когда система не получает извне определенную энергию тогда теплота всегда переходит от более нагретых тел к менее нагретым телам.
Во всех этих формулировках строго следует обратить внимание на то, где говорится про единственный конечный результат , который имеет важное практическое значение, иначе можно было бы создать двигатель, который работал бы совершая работу за счет полученной извне теплоты. Вот где главная сущность второго начала термодинамики [6].
Многие школьники, студенты, магистранты при изучении этой темы не вникают в сущность проблемы, до конца не представляют значение второго начала термодинамики, все эти формулировки получены на основе эмпирических данных и представляют один из главных законов природы.
Теперь попробуем разобраться сначала с понятием энтропии, затем приступим к закону возрастания энтропии. Что с собой представляет энтропия и для чего его ввели в физику?
В физике часто приходится иметь дело с понятием вероятности, поэтому вероятность макросостояния определяется его статистическим весом, т.е. набором многих микросостояний которые определяют одно макросостояние. Обычно статистический вес выражается огромными числами, поэтому берут его натуральный логарифм, значит выражают следующей формулой
.
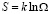Значит для характеристики вероятности состояния системы используют понятие энтропии системы, энтропия является вообще говоря функцией термодинамической системы, т.е. она представляется как функция следующих параметров: давления, обьема, температуры, плотности и т.д. Энтропия определяется следующей формулой:
.
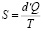При рассмотрении многих тепловых процессов, различных изопроцессов, тепловых машин такое определение энтропии используется в основе термодинамических соотношений [6].
Энтропия показывает, что в природе все процессы протекают таким образом, система всегда переходит из менее вероятного состояния в более вероятное состояние, например передача теплоты от горячего тела к холодному, распространение газа из одной половинки сосуда на весь обьем сосуда и т.д. С такими примерами мы на практике сталкиваемся постоянно, значит вероятности различных переходов очень сильно отличаются, например переход теплоты от холодного тела к горячему мы не наблюдаем если нет внешней поступающей теплоты.
Теперь рассмотрим обратимые и необратимые процессы. Известно, что в природе многие процессы необратимые, а в ходе необратимого процесса для изолированной системы энтропия всегда возрастает, значит она переходит из менее вероятного в более вероятное состояние.
.
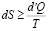В таких процессах как известно увеличивается статистический вес системы, значит и энтропия возрастает.
Для обратимых процессов, которые находятся в равновесном состоянии энтропия изолированной системы всегда будет максимальной [1–4].
Вот эти оба утверждения, что энтропия изолированной термодинамической системы может только возрастать либо по достижении максимума оставаться постоянной называют законом возрастания энтропии или второго начала термодинамики. Значит закон возрастания энтропии выполняется для изолированной системы. для изолированной системы количество теплоты в систему не поступает, для обратимых процессов изменение энтропии равно нулю, значит энтропия остается постоянной. Отсюда видим, что в ходе обратимого процесса для изолированной системы энтропия остается постоянной. Отсюда мы видим, что для необратимого процесса энтропия изолированной системы всегда возрастает, энтропия никогда не уменьшается. Вот здесь надо обратить внимание на то, что мы рассматриваем строго изолированную систему.
Второе начало термодинамики выражает особенности закономерности явлений, связанных тепловым движением. Второе начало термодинамики приводит к существованию и возрастанию энтропии, имеет место как в больших, так и в малых телах. Вообще говоря второе начало термодинамики, все законы термодинамики неприменимы к микросистемам. Это не означает, что в таких системах нарушается второе начало,--вечный двигатель второго рода осуществить нельзя с помощью любых систем. Можно указать также и верхнюю границу применимости законов термодинамики. Статистическую природу второго начала термодинамики впервые установил выдающийся физик Больцман. Состояние термодинамического равновесия, по Больцману является лишь наиболее часто встречающимся, наиболее вероятным, в равновесной системе всегда самопроизвольно могут возникнуть сколь угодно большие флуктуации [5].
Все эти утверждения и выводы относятся ко Вселенной, в ней неизбежно возникают большие флуктуации. Наблюдения и открытия астрофизики показывает возникновение и развитие звездных ассоциаций, материя обладает никогда не утрачиваемой способностью к концентрации энергии и превращению одних форм в другие формы. Одним словом применительно ко Вселенной мы не можем говорить о законе возрастание энтропии [5].
Смысл закона возрастания энтропии или второго начала термодинамики вкратце обьяснили, а приведенные примеры мы знаем из практики, как протекают процессы при передаче теплоты, вероятности различных переходов из менее вероятной в более вероятное состояние можно таким путем обьяснить [1–3].
Теперь попробуем рассмотреть закон возрастания энтропии применительно ко Вселенной, ко всем явлениям происходящим в мире.
Все сказанное выше особенно возрастание энтропии, переход в состояние с большей энтропией, переход замкнутой системы в состояние статистического равновесия мы реально наблюдаем на практике, в повседневной жизни. Если реально говорить о переходе в состояние с большей энтропией, то оно по сравнению с переходом в состояние с меньшей энтропией настолько очень велико, что о последнем можно и не говорить даже.
Значит, если замкнутая система в некоторый момент времени находится в неравновесном макроскопическом состоянии, то наиболее вероятным следствием в последующие моменты времени будет монотонное возрастание энтропии системы. Это есть так называемый закон возрастания энтропии или второй закон термодинамики. Он был открыт Р. Клаузиусом, а его статистическое обоснование было дано Л. Больцманом.
В справедливости выше сказанных законов мы не сомневаемся, они имеют свое подтверждение на практике, мы каждый день наблюдаем эти закономерности в повседневной жизни. Однако если применить эти закономерности в целом ко Вселенной, к миру в целом, тогда возникают существенные затруднения, которые не имеют конкретного решения.
Как известно, по определению статистической физики любая замкнутая статистическая система с течением времени должна находиться в состоянии полного статистического равновесия. Всем известно, что в природе очень много флуктуационных явлений, они не имеют ничего общего со свойствами равновесной системы, например на Земле в одних местах наблюдаем высокотемпературные магмы, в других местах аномальная низкая температура, но со времени существования Земли они никогда не достигли состояния полного статистического равновесия и на вряд ли это будет достигнуто. То же самое можно сказать и о свойствах Вселенной где наряду с высокотемпературными состояниями наблюдаются и состояния с очень низкими температурами, существования таких флуктуационных состояний это и есть условие существования жизни на планете, условие для развития биологических организмов [1-3].
Здесь самое главное отличие в том, что мы рассматриваем закон возрастание энтропии для замкнутых систем, термодинамические системы на Земле и во Вселенной являются незамкнутыми, где очень много флуктуационных явлений, это бесконечные процессы которые продолжаются уже несколько миллиардов лет и никто не может сказать где начало и где конец всего этого явления.
Согласно последним научным теоретическим данным в астрофизике Вселенная возникла после «Большого Взрыва» примерно 13,5–14 миллиардов лет назад, с тех пор она продолжает расширяться. Все эти флуктуационные явления происходят во Вселенной непрерывно, можно сказать, что это почти бесконечный промежуток времени.
Таким образом получается не соответствие одного из основных законов физики с глобальными явлениями природы и Вселенной в целом, возможно эти противоречия будут решены через несколько тысячелетий, но прежде хотелось бы поискать основные причины этого не соответствия, попробуем выделить несколько основных главных факторов влияющих на эти расхождения теории и практики.
Во-первых здесь обязательно огромную роль играют выводы теории относительности, свойства гравитационных полей. Известно, что в общей теории относительности изменяется метрика пространства, происходит искривление пространства, где изменяется метрический тензор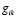 
, оно зависит и от координат и от времени. Вот эти изменения метрики пространства и времени многие не понимают до конца, потому что в школе и в ВУЗе все мы используем евклидову геометрию, где сумма углов в треугольнике равняется 180 градусов, где параллельные прямые никогда не пересекаются, сумма углов в четыркхугольнике равняется 360 градусов и т.д. А в гравитационном поле где происходит искривление пространства используется геометрия Лобачевкого. Это может быть одним из главных факторов, если не самый главный фактор, то в любом случае он играет определенную роль в этом случае. Значит здесь нужно учитывать изменение метрики пространства, изменение метрического тензора 
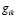в общей теории относительности А. Эйнштейна [1-3].
Во-вторых как мы знаем уравнения классической механики полностью симметричны по отношению к обоим направления времени, значит и в законе возрастания энтропии тоже должен быть и обратный закон, который приводит к уменьшению энтропии, возможно это осуществится через огромный промежуток времени, но как мы знаем из практики обратное уменьшение энтропии никогда не наблюдается в природе вообще. Из симметричности уравнений классической механики, одного из разделов физики, естественно мы не можем сделать такое обобщение,что если в природе наблюдается возрастание энтропии,то мы должны наблюдать и уменьшение энтропии.
В третьих известно, что в уравнениях Максвелла имеются и симметричные части, и не симметричные части, так что говорить о полной симметрии нельзя, так как в природе встречается и то, и другое, также как волновая и корпускулярная природа света
В уравнениях Максвелла, при рассмотрении ее в дифференциальной форме электрическое и магнитное поле описываются аналогичными уравнениями, но некоторые не имеют симметрию, например для магнитного поля отсутствует магнитный заряд, для электрическог поля источником поля служит электрический заряд. Симметрия или антисимметрия многих законов природы требует естественно досконального изучения физических процессов.
В четвертых, как известно при наблюдении всех изменений природы, при наблюдении за флуктуационными изменениями в природе несомненно участвует налюдатель, а наблюдатель это тоже часть природы, так что надо ввести систему отсчета вместе с наблюдателем, а время релаксации перехода системы в стационарное состояние может быть разным и огромным [1-3].
В пятых, как известно в квантовой механике наблюдается неэквивалентность обоих направлений времени, а уравнения Шредингера основное уравнение квантовой механики симметрично по отношению к изменению знака времени. Неэквивалентность обоих направлений времени проявляется когда мы наблюдаем процесс взаимодействия микрообьекта с классическим обьектом, возможно этот фактор является главным звеном для проявления основного закона термодинамики закона возрастания энтропии. В целом в природе, в жизни человека мы больше наблюдаем односторонние, необратимые процессы, значит возрастание энтропии логически должно протекать только в одном направлении. Здесь надо учитывать самый главный фактор то,что мы закон возрастание энтропии рассматриваем только в замкнутых системах, а Вселенная как известно, является не замкнутой системой.
В шестых, возможно для решения всех этих противоречий не нашли еще главного закона природы, где в предельном случае досконально рассматриваются все эти факторы, а в главном законе должны фигурировать такие величины как постоянная Планка, скорость света в вакууме, постоянная Больцмана и т.д.
В седьмых, возможно еще есть какой-то главный фактор о существований которого мы не знаем или не учитываем, возможно это такая закономерность которая не имеет аналогов в классической механике.
Сделаем общий вывод всех этих рассуждений: законы природы не исследованы до конца, они требуют глубоких знаний и скурпулезных исследований, анализов экспериментальных и теоретических данных полученных человечеством за всю историю науки [1–3].
В заключение приведем общую формулировку закона возрастания энтропии: во всех осуществляющихся в природе замкнутых системах энтропия никогда не убывает-она увеличивается или, в предельном случае, остается постоянной.
.
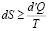Соответственно аналогично этим двум закономерностям в природе принято делить процессы на необратимые и обратимые. для необратимых процессов в замкнутой системе энтропия ворастает, а для обратимых процессов в замкнутой системе энтропия остается постоянной.