Фазовая диаграмма системы Сu-Pb-Tl изучена в работе [1]. Граничные системы Cu-Pb и Cu-Tl характеризуются областью несмешиваемости в жидкой фазе [2]. В системе Cu-Pb при температуре монотектического равновесия 955°С расслаивание охватывает область составов xCu=0.35÷0.845, критическая температура растворимости равна 9950C. В системе Cu-Tl при температуре монотектики 968°С расслаивание имеет место в области концентраций xCu=0.17÷0.855, при этом критическая температура растворимости равна 1260°C. В работе [3] проведен расчет и моделирование поверхности расслаивания жидкой фазы в тройной системе Сu-Pb-Tl в интервале температур 955-1260°C и концентраций xCu=0.17÷0.855.
Целю данной работы является моделирование и визуалирование поверхности кристаллизации меди в тройной системе Сu-Pb-Tl. Использована расчетная методика, описанная в работах [3,4,5]. Уравнение аналитической модели поверхности ликвидуса имеет вид
Т(1-2-3)(x,y)=y2 Т1(12) (х1)+ +(1–y2)Т1(13) (х1)+aх1(1–х1)2y2(1–y2), (1)
где Т – температура, К; y2= x2/(1–х1); (1–y2)=x3/(1–х1); a – определяется по 3-5 измерениям ДТА для тройной системы. Т1(12) (х1) и Т1(13)(х1) –аналитические выражения ликвидуса двойных граничных систем.
Для расчета и визуалирования поверхности ликвидуса меди с помощью программы grafikus.ru/plot3d использован способ описания состава, приведенный на рис. 1б. В этом случае x1–мольная доля компонента 1,
y2(23)=x2/(x2+х3)=x2/(1–х1). (2)
Эти два параметра достаточны для представления состава тройной системы, так как x2=y2/(1–х1) и x3=1–x2–x3. В более общей форме выражение (2) можно представить в виде
yj(jk)=xj/(xj+хk)=xj/(1– хi),
где xi –мольная доля компонента i. Представление составов тройной системы в такой форме (рис. 1б) позволяет представить результаты расчетов функции Т(x,y) в трехмерных координатах (рис. 3–5).
Уравнение (1) применительно к системе Cu-Pb-Tl имеет вид
Т(Cu-Pb-Tl)=yPbТ(Cu–Pb)(хCu)+ +(1–yPb)Т(Cu-Tl)(хCu)+ +aхCu(1–хCu)yPb(1–yPb), (3)
где yPb= xPb/(1–хCu); (1–yPb)=xTl/(1–хPb).
T (Cu-Tl)=1358–1130x2(1–x); (4)
Т (Cu-Pb)= 1358–1450x3(1–x). (5)
Соотношения (4) и (5) с высокой точностью аппроксимируют кривые ликвидуса меди в двойных граничных системах Cu-Pb и Cu-Tl (таблица). Подставляя аналитические выражения кривых ликвидуса меди в двойных граничных системах и значение величины а в уравнение (3) получаем:
T(Сu-Tl–Pb)=1358– –1130x2(1–x)y–1450x3(1–x)(1–y)+ +40хCu(1–хCu)yPb(1–yPb), (6)
где x=xCu, y=xPb/(xPb+ xPb).
Поверхность кристаллизации меди в тройной системе Cu–Pb–Tl в интервале концентрации xCu=0.845÷1.0, вычисленная по уравнению (6), визуалирована на рис. 2.
а б
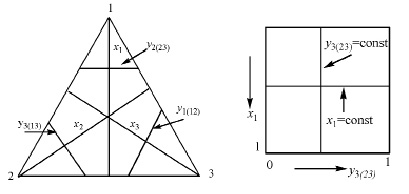
Рис. 1. Способы представления составов тройной системы
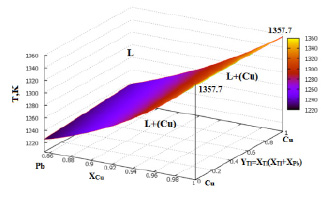
Рис. 2. Поверхность ликвидуса меди в системе Cu-Pb-Tl в интервале концентрации xCu=0.845÷1.0
Экспериментальные и расчетные данные для кривых кристаллизации меди в системах Cu-Pb и Cu–Tl в интервале концентрации xCu=0.845÷1.0.
|
хCu(Cu-Tl) |
Т, К |
хCu (Cu-Pb) |
Т, К |
||
|
эксп. [2] |
Расчет (3) |
эксп. [2] |
Расчет (4) |
||
|
1.0 0.95 0.90 0.845 |
1358 1296 1258 1241 |
1358 1307 1266 1238 |
1.0 0.95 0.90 0.845 |
1358 1290 1247 1228 |
1358 1295 1252 1224 |
Для расчета поверхности кристаллизации меди в в тройной системе Cu–Pb–Tl в интервале концентрации xCu=0÷0.2 использован следующий подход. Вначале определили аналитическое выражение кривой ликвидуса твердых растворов TlxPb1-x в системе Tl–Pb:
T, K=(601+402y1.6)(1–y)0.3, (6)
где y=xTl/(xPb+xPb). Далее по экспериментальным данным трех симметрично расположенных составов тройной системы определили функцию зависимости температуры ликвидуса от концентрации меди:
T, K=(601+402y1.6)(1–y)0.3+ +41600x(1–x)4y(1–y), (7)
которая позволила с высокой точностью (до 5°) вычислить и визуалировать поверхность кристаллизации меди в тройной системе Cu–Pb–Tl в интервале концентрации xCu=0÷0.2 (рис. 3,4).
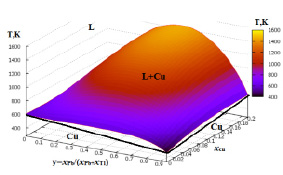
Рис. 3. Поверхность ликвидуса меди в системе Cu-Pb-Tl в интервале концентрации xCu=0÷0.2
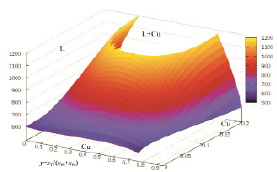
Рис. 4. Поверхность ликвидуса меди в системе Cu-Pb-Tl в интервале концентрации xCu=0÷0.2 ниже 1200 К
Особенность поверхности ликвидуса на рис. 2-4 состоит в том, что компонент Cu представлен линией. Несмотря на это, точки на поверхности точно отражают состав тройной системы при соответствующем значении температуры ликвидуса.
Таким образом, на основании аналитических выражений кривых ликвидуса двойных граничных систем с использованием ограниченного числа данных ДТА решена задача 3D моделирования поверхности кристаллизации меди в тройной системе Cu-Pb-Tl. Эти данные вместе с аналитическим выражением поверхности расслоения жидкой фазы [3], представляют 3D модель фазовой диаграммы системы Cu-Pb-Tl.



