Связанные микрополосковые линии, имеющие малые размеры, широко применяются для создания различных устройств, таких как фильтры, направленные ответвители, элементы согласования комплексных сопротивлений, линии задержки [6], [8]. Применение высокотемпературных сверхпроводников для изготовления микрополосковых линий позволяет существенно уменьшить потери по сравнению с микрополосковыми линиями на обычных проводниках [2, 3].
В связанных линиях имеется три проводника: две параллельные полоски и экран (или заземленная пластина). Рассмотрим следующую геометрию связанной микрополосковой линии: две полоски шириной W из высокотемпературного сверхпроводника расположены на расстоянии s друг от друга на подложке из диэлектрика с высокой диэлектрической проницаемостью толщиной h. Диэлектрическая положка разделяет сверхпроводящие полоски и проводящий экран, которые может быть выполнен как из сверхпроводящего материала, так и из обычного проводника. Толщина сверхпроводящих полосок d. Предполагается, что сверхпроводящие полоски находятся в сверхпроводящем состоянии, соответственно температура T<Tc, где Tc – критическая температура для используемого сверхпроводника.
Температурная модель
Рассмотрим феноменологическую модель, теоретически описывающую параметры рассматриваемой микрополосковой линии, приведенную в работах [1, 5]. Модель применима в случае, если глубина проникновения поля в проводник много меньше толщины диэлектрической подложки h, на которую нанесены связанные проводники и заземленная пластина. Как правило, это приближение выполняется в практически используемых структурах связанных микрополосковых линий. Параметры модели являются подгоночными и определяются из сравнения с экспериментальными результатами, полученными для тонких пленок высокотемпературных сверхпроводников, из которых выполнены полоски линии. Для расчета характеристик микрополосковой линии необходимо знание поверхностного импеданса. В рамках предложенной в работах [1, 5] модели поверхностный импеданс записывается в виде:
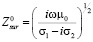 , (1)
, (1)
где w=2πf, f – частота, µ0 – магнитная постоянная, s=σ1–iσ2 – удельная проводимость сверхпроводника, которая в рамках используемой модели имеет следующую температурную зависимость [5]:
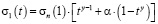 , (2)
, (2)
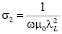 , (3)
, (3)
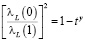 , (4)
, (4)
Здесь σn(1) – проводимость нормальных носителей заряда при температуре Tc, t = T/TC – приведенная температура, T – температура, lL – лондоновская глубина проникновения магнитного поля в сверхпроводник, lL(0)=0,13⋅10-6⋅exp(1,27–0,5g), a – параметр остаточного сопротивления и g – эмпирический параметр, определяющий температурную зависимость лондоновской глубины проникновения. Модель использует следующие феноменологические параметры: Tc, σn(1), a и g. В случае использования сверхпроводника в виде тонкой пленки необходимо учитывать отражение электромагнитной волны от обеих границ плёнки и рассчитывать поверхностный импеданс по формуле [1]:
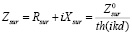 , (5)
, (5)
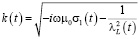 . (6)
. (6)
Для описания линии передачи из высокотемпературных сверхпроводников используются следующие параметры: волновое сопротивление Z0, волновое число b и коэффициент затухания αat. Волновое число b в микрополосковой линии рассчитывается по формуле:
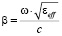 , (7)
, (7)
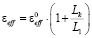 , (8)
, (8)
Здесь εeff – эффективная проницаемость подложки, εeff0 – эффективная проницаемость подложки без учета вклада сверхпроводника, Lk – кинетическая индуктивность сверхпроводника, L1 – погонная индуктивность линии передачи. Кинетическая индуктивность сверхпроводника рассчитывалась в соответствии с подходом, предложенным в работе [7]. Кинетическая индуктивность для нечетной моды рассчитывалась по формуле
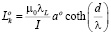 , (9)
, (9)
для четной моды
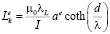 , (10)
, (10)
где
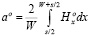 , (11)
, (11)
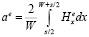 , (12)
, (12)
W – ширина полоскового сверхпроводника, s – расстояние между полосками, 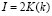 , K(k) – полный эллиптический интеграл [7],
, K(k) – полный эллиптический интеграл [7], 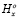 и
и 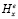 – x – компонента магнитного поля для нечетной и четной моды, рассчитанная в соответствии с работой [7].
– x – компонента магнитного поля для нечетной и четной моды, рассчитанная в соответствии с работой [7].
Коэффициент затухания определяется выражением:
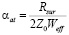 , (13)
, (13)
где 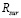 – действительная часть поверхностного импеданса сверхпроводящей пленки, Weff – эффективная ширина проводника линии с учетом неравномерного распределения плотности поверхностного тока по ширине проводника [5].
– действительная часть поверхностного импеданса сверхпроводящей пленки, Weff – эффективная ширина проводника линии с учетом неравномерного распределения плотности поверхностного тока по ширине проводника [5].
Зависимость кинетической индуктивности от температуры определяется температурной зависимостью лондоновской глубины проникновения магнитного поля в сверхпроводник. Как показано в работе [5], вклад кинетической индуктивности в эффективную диэлектрическую проницаемость микрополосковой линии, образующей резонатор, определяет зависимость резонансной частоты сверхпроводящих резонаторов от температуры. Целью данной работы является исследование коэффициента передачи сверхпроводящей полосовой линии и возможность управления коэффициентом передачи при изменении температуры.
Результаты расчетов
Расчеты проводились для двух связанных полосок из высокотемпературного сверхпроводника YBa2Cu3O7. На рисунках 1 и 2 представлены результаты расчета коэффициента передачи, проведенного в соответствии с формулами (1 – 13). Для расчетов использовались следующие параметры: 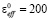 , g=2.1, a=5.2, σn(1)=1.7⋅108 Ом×м, Тс=88 К, εeff=9,8, d=0,25 мкм. На рис. 1 показана температурная зависимость коэффициента прохождения T для микрополосковой линии.
, g=2.1, a=5.2, σn(1)=1.7⋅108 Ом×м, Тс=88 К, εeff=9,8, d=0,25 мкм. На рис. 1 показана температурная зависимость коэффициента прохождения T для микрополосковой линии.
Из рис. 1 видно, что изменение температуры оказывает заметное величину на величину коэффициента прохождения. Наиболее заметное изменение наблюдается при температурах, чуть ниже критической в диапазоне 0.7×Тc<T< Тc. Причем, изменение частоты оказывает влияние на поведение коэффициента прохождения. При частоте ω=5⋅1014 рад/с коэффициент передачи уменьшается с ростом температуры, а при частоте ω=6⋅1014 рад/с возрастает.
На рис. 2 представлена частотная зависимость коэффициента передачи. Качественная зависимость коэффициента передачи соответствует экспериментальным данным для связанной микрополосковой линии, приведенным в работе [4]. При увеличении температуры полоса пропускания полосковой линии смещается в сторону более низких частот.
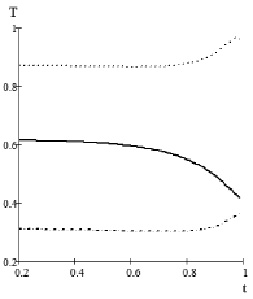
Рис. 1. График зависимости коэффициента прохождения Т от приведенной температуры для разных частот. Сплошная кривая: ω=5⋅1014 рад/с, пунктирная кривая: ω=6⋅1014 рад/с, точечная кривая: ω=8⋅1014 рад/с
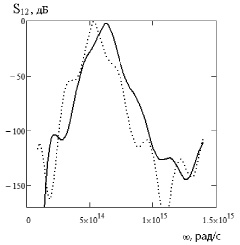
Рис. 2. График зависимости коэффициента передачи от частоты для высокотемпературного микрополоскового резонатора. Сплошная линия: Т=0.7 Тс, пунктирная линия: Т=0.98 Тс.
Особый интерес представляет зависимость коэффициента передачи для значений температур вблизи критической (пунктирная кривая). Как показано в работе [5], при увеличении температуры и приближении ее к критической коэффициент передачи существенно уменьшается. Как видно из рисунка 2 (пунктирная кривая) в случае повышения температуры соответствующий подбор параметров микрополосковой линии (толщины сверхпроводящей пленки, размеров полосок и расстояния между ними) приводит к тому, что сверхпроводящая микрополосковая линия демонстрирует большие значения коэффициента передачи даже при высоких температурах. Таким образом, результаты расчетов, проведенных в данной работе, говорят о возможности температурной перестройки параметров полосковой линии на основе высокотемпературных сверхпроводников и о возможности работы такой линии при температурах, близких к критической.
Выводы
В работе проведен теоретический расчет электродинамических характеристик микрополосковой связанной линии на основе тонких пленок высокотемпературных сверхпроводников. Показана возможность температурного управления коэффициентом передачи микрополосковой линии. В работе продемонстрировано, что соответствующий подбор параметров микрополосковой линии дает возможность ее использования при температурах, близких к критической температуре для сверхпроводника. Результаты, полученные в работе, показывают перспективность применения высокотемпературных сверхпроводников с малыми потерями в оптоэлектронных устройствах, например фильтрах, параметры которых можно менять при изменении температуры.



