Одним из наиболее перспективных направлений развития информационных технологий является широкое проникновение систем электронных платежей (СЭП) практически во все сферы деятельности современного государства. Однако при этом использование таких информационных технологий непосредственно связано с определенной совокупностью рисков, основой причиной которых являются уязвимости информационных технологий и систем.
Как правило, вопросы защиты денежных средств электронных коммерческих систем возлагается на протоколы криптографической защиты. Именно их стойкость во многом определяет степень защищенности электронных денег. В работе рассмотрены вопросы защита данных в электронных коммерческих системах на основе использования модулярных структур.
Современный этап развития электронных коммерческих систем предопределяет все более широкое применение универсальных платежных средств, таких как электронные деньги. Это обусловлено достоинствами электронных платежных средств, среди которых можно выделить [1-3]:
- очень низкая стоимость эмиссии электронных денег;
- превосходная делимость и объединяемость;
- высокая портативность;
- снижается воздействие человеческого фактора;
- более высокая степень защищенности от хищения, подделки, изменения номинала.
При постоянно расширяющихся возможностях электронных коммерческих систем широкое внедрение электронных денег пока не наблюдается. Это обусловлено целым рядом причин, основными из которых являются:
- сложность обеспечения вопросов сохранения анонимности пользователя – владельца электронных денежных средств;
- необходимость постоянной защиты передаваемых данных между пользователями протокола обмена от несанкционированного доступа;
- сложность протоколов, используемых в системах электронной коммерции.
Для решения отмеченных проблем в ряде работ предлагается использовать алгебраические модулярные структуры. Проведенные исследования показали, что такие системы обладают более широкими возможностями по реализации различных линейных и нелинейных криптографических функций [4]
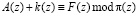 , (1)
, (1)
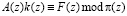 , (2)
, (2)
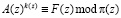 , (3)
, (3)
где 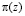 – неприводимый полином, порождающей поле GF(q); q = pv; р – простое число; A(z) – блок открытого текста длиной v разрядов; F(z) – блок зашифрованного текста длиной v разрядов;
– неприводимый полином, порождающей поле GF(q); q = pv; р – простое число; A(z) – блок открытого текста длиной v разрядов; F(z) – блок зашифрованного текста длиной v разрядов; 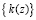 – множество ключевых данных.
– множество ключевых данных.
В работах [5-8] представлен алгоритм нелинейного шифрования потока данных, использующий операцию возведения в степень символов конечного поля. При этом с целью сокращения времени зашифрования потока открытых данных предлагается использовать полиномиальную систему классов вычетов (ПСКВ). В данной непозиционной системе в качестве оснований используются неприводимые полиномы 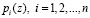 , произведение которых дает рабочий диапазон системы
, произведение которых дает рабочий диапазон системы
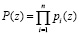 . (4)
. (4)
Для реализации алгоритма входной поток битов разбивается на отдельные блоки, двоичный код которых представляется в полиномиальной форме А(z). В этом случае размер блока выбирается из условия
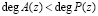 . (5)
. (5)
Так как рабочий диапазон Р(z) представляет собой кольцо неприводимых полиномов, то на основе изоморфизма, порожденного китайской теоремой об остатках, что каждый блок A(z), можно однозначно представить в виде
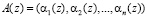 . (6)
. (6)
В этом случае выражение (3) можно представить следующим образом
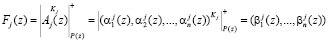 , (7)
, (7)
где 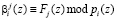 ;
; 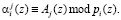
Так как сравнения по одному и тому же модулю можно почленно умножать, то последнее выражение представляется в виде:
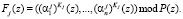 (8)
(8)
Представленные результаты исследования показали, что использование ПСКВ для реализации защиты информации от НСД позволяет повысить быстродействие более чем на 9% по сравнению с выполнением метода шифрования с возведением в степень по модулю в поле Галуа 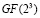 . При этом при увеличении разрядности обрабатываемых данных возрастает эффективность применения ПСКВ для реализации нелинейных криптографических процедур защиты данных от НСД.
. При этом при увеличении разрядности обрабатываемых данных возрастает эффективность применения ПСКВ для реализации нелинейных криптографических процедур защиты данных от НСД.
С целью решения первого и третьего недостатков в системах электронной коммерции все больше используются различные протоколы доказательства с нулевым разглашением. Применение таких протоколов позволяет владельцу электронной наличности доказать банку свою правомочность использования электронных денег и получить от него кошелек с электронными монетами [2].
При этом протоколы доказательства с нулевым разглашением не предоставляют банку никакой информации о секретном ключе пользователя, а только убедить банк, что клиент действительно владеет таким ключом. Известно [1-3], что основным преимуществом протоколов доказательства с нулевым разглашением является то, что проверяющая сторона не может получить никакой полезной информации о секретном ключе пользователя. Для того чтобы снизить вероятность ошибочного опознания, проверяющая сторона может задавать подряд несколько вопросов. Все это приводит к снижению эффективности работы систем коммерческих расчетов. В работе [1] приведен пример итерационного алгоритма протокола доказательства с нулевым разглашением. Покупатель, будучи легальным пользователем системы, обладает секретным (закрытым) ключом Ксекр и соответствующим ему открытым ключом Котк. При этом значение последнего определяется
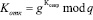 , (9)
, (9)
где q – порядок мультипликативной группы с порождающим элементом g. Для того, чтоб убедить банк в том, что он и есть обладатель открытого ключа Котк, ему необходимо доказать, что он знает Ксекр.
Для этого пользователь выбирает некоторое случайное число r, вычисляет значение
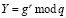 . (10)
. (10)
Вычисленное значение пересылается банку. Проверяющая сторона выбирает число В из мультипликативной группы и пересылает его пользователю, т.е. «задает ему вопрос В». Получив «вопрос» с, пользователь должен на него вычислить «ответ» согласно равенства
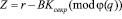 . (11)
. (11)
Полученный результат пересылается банку, который осуществляет проверку полномочий пользователя согласно
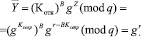 (12)
(12)
Затем производится сравнение с принятым ранее значением Y.
Основным недостатком данного алгоритма является низкая скорость проверки авторизованного пользователя из-за интерактивного обмена сообщениями между сторонами. Решить данную проблему можно за счет применения псевдослучайной функции, которая бы позволила создавать вопрос и находить ответ на одной стороне пользователя. При этом пользователь пересылает только ответы банку.
Как правило, такие процедуры носят итерационный характер. Такая многоэтапная процедура обмена позволяет банку убедиться в истинности намерений пользователя. Однако при значительном увеличении числа пользователей электронными деньгами это может привести к значительной временной задержке. Решить данную проблему можно за счет применения псевдослучайной функции (ПСФ) повышенной эффективности.
В работах [1-3] приведены примеры реализации псевдослучайной функции обладающей повышенной эффективностью. Следует отметить, что ПСФ нашли широкое применение и в других сферах. Так в работах [9,10] показано применение псевдослучайных функций в системах опознавания статуса спутника системы космической связи, используемой при управлении удаленным экологически-опасными объектами. Проведенные исследования показали, что применение разработанной псевдослучайной функции позволяет обеспечить сложность решения λ-DDH проблемы. Кроме того, одним из основных преимуществ данной ПСФ является использование меньшего объема памяти для вычисления значения функция, так как она использует ключ в log2 l раз меньший размером по сравнения с ПСФ Наора-Рейнголда.
Алгоритм применения разработанной псевдослучайной функции в протоколе доказательства с нулевым разглашением состоит из следующих этапов. На первом этапе проверяющая сторона пересылает пользователю случайное число S. Затем последний выбирает случайное число r и вычисляет соответствующее ему значение 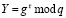 . Затем пользователь сам задает себе «вопрос» В
. Затем пользователь сам задает себе «вопрос» В
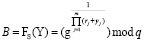 , (13)
, (13)
где yj и rj – j-й блок, полученный при разбиении чисел Y и S на m частей.
На поставленный вопрос пользователь вычисляет ответ согласно (11). Затем, используя свой секретный ключ, закрывает данные 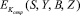 и пересылает полученный зашифрованный текст банку. Банк может убедиться в правильности данной подписи, применяя открытый ключ пользователя Котк.
и пересылает полученный зашифрованный текст банку. Банк может убедиться в правильности данной подписи, применяя открытый ключ пользователя Котк.
Пример. Пусть задана мультипликативная группа G11. В данной группе существует первообразный элемент g = 2. В качестве секретного ключа пользователь выбираем Ксекр= 3. Тогда открытый ключ определяется согласно (1) и составит
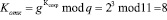 .
.
Чтобы доказать банку, что он владеет секретным ключом, пользователь выбирает число r = 5 и вычисляет
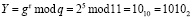 .
.
Разбиваем вычисленное число на два подблока у1 = 102 = 2 и у2 =102=2. Для проверки пользователя банк прислал случайное число S = 6, которое в двоичном коде представляется как 0110. Двоичный код числа S = 01102 разбивается на два подблока s1 =012=110 и s1 = 102=210. Затем пользователю, используя полученные выше числа, необходимо вычислить вопрос В согласно (11). Имеем
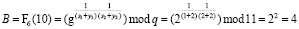 .
.
Таким образом, значение вопроса В = 2.
Вычислив свой вопрос, пользователь приступает к вычислениям ответа на данный вопрос, используя r = 5 и Ксекр= 3. При этом используется выражение (11). Тогда
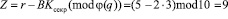 .
.
Затем, используя свой секретный ключ, пользователь закрывает данные 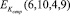 и пересылает полученный зашифрованный текст банку. Банк, применяет открытый ключ пользователя Котк и получает все зашифрованные значения чисел. Эти значения позволят получателю убедиться в правильности данной подписи. При этом используется выражение (12)
и пересылает полученный зашифрованный текст банку. Банк, применяет открытый ключ пользователя Котк и получает все зашифрованные значения чисел. Эти значения позволят получателю убедиться в правильности данной подписи. При этом используется выражение (12)
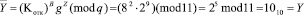 .
.
Таким образом, применение разработанной псевдослучайной функции позволило выполнить протокол доказательства с нулевым разглашением.
Выводы
В работе рассмотрены вопросы связанные с обеспечением защиты передаваемых в системах электронной коммерции. Представлен алгоритм нелинейного шифрования с использованием полиномиальной системы классов вычетов. Использование непозиционной системы класса вычетов позволяет повысить скорость выполнения операции зашифрования. Показана целесообразность применения псевдослучайной функции в протоколе аутентификации пользователя в банке. В статье рассмотрен пример реализации протокола с нулевым доказательством на основе псевдослучайной функции.



