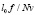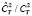В данной статье будут рассмотрено несколько аспектов влияния масштабов атмосферной турбулентности, а именно, внешнего и внутреннего масштабов, на оценку уровня турбулентного развития.
Важность внешнего масштаба турбулентности
В первую очередь рассмотрим здесь вопросы влияния внешнего масштаба на дисперсию флуктуаций температуры (или показателя преломления). Известно, что распределение энергии в турбулентности определяется спектральной плотностью флуктуаций показателя преломления Фn(κ). Поскольку реальные турбулентные неоднородности трехмерны, то при оценке дисперсии флуктуаций показателя преломления необходимо вычислять [1] функционал следующего вида:
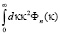, (1)
где Фn(κ) – спектральная плотность флуктуаций показателя преломления атмосферы, κ – пространственное волновое число (или величина обратная размеру турбулентной неоднородности).
Предварительно отметим, что функционал (1) пропорционален дисперсии флуктуаций показателя преломления. Сравним функционалы вида (1) для двух спектров атмосферной турбулентности [2, 3] в предположении их изотропности, а именно,
– кармановскую модель с колмогоровским наклоном спектра
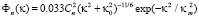, (2)
– и когерентный спектр следующего вида
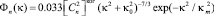. (3)
Здесь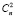 
– структурный параметр показателя преломления для колмогоровской турбулентности, 
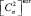– структурный параметр показателя преломления для когерентной турбулентности κ0 = 2π/L0 – волновое число, соответствующее внешнему масштабу турбулентности L0, κm = 5,92/l0 – волновое число, соответствующее внутреннему масштабу турбулентности l0.
Проведем расчет интеграла (1), т.е. дисперсии флуктуаций показателя преломления для модели (2), имеем
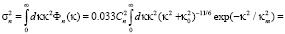
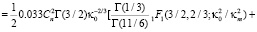
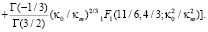
При условии, что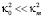 
, для кармановской модели (2), получаем
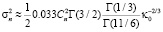. (4)
В тех же условиях для когерентного спектра вида (3) получаем, что
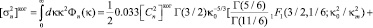
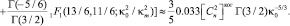(5)
Приравняв дисперсии (4) и (5), получаем, что
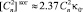(6)
Далее, исходя из формул (3)–(5), имеем, что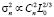 
, а так как, согласно модели В.И. Татарского [3] вида 
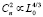, получаем, что 
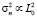. При этих же предположениях для когерентной турбулентности (т.е. для модели (3)) 
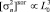. Это позволяет заключить, что в когерентной турбулентности энергия сильнее, по сравнению с Колмогоровской моделью, зависит от размера внешнего масштаба турбулентности L0, а это указывает на фактическую важность знания величины такого масштаба для оценки энергии турбулентности.
Влияние внутреннего масштаба турбулентности на погрешности оценки структурного параметра показателя преломления
В течение ряда лет в Институте оптики атмосферы им. В.Е. Зуева СО РАН (ИОА СО РАН) проводятся сопоставительные измерения структурной постоянной показателя преломления воздуха оптическими методами и акустическим методом. На основе данных, полученных в результате комплексного эксперимента на Базовом экспериментальном комплексе ИОА СО РАН в июле – августе 2013 г., проведено сравнение оценок структурной постоянной показателя преломления воздуха, характеризующей интенсивность атмосферной турбулентности, из оптических измерений выполненных, дифференциальным измерителем турбулентности (ДИТ) [4, 5] и датчиком волнового фронта, работающим по схеме Шека-Гартмана [6, 7]. Измерения проводились на приземных однородных, разнесенных по горизонтали на расстояние 96 см, оптических трассах протяжённостью 200 м примерно на высоте 160–170 см над подстилающей поверхностью. Оптические измерения сопровождались измерениями метеопараметров атмосферы двумя ультразвуковыми метеостанциями АМК-03 [9] и »Метео-2» [9].
Метеостанция АМК-03 располагалась вблизи приёмного устройства ДИТ и ДВФ на высоте 170 см, а станция «Метео-2» – на расстоянии 60 м от приёмного устройства вдоль оптической трассы и была вынесена на 10 м от оптической оси оптического измерителя ДИТ на высоте 2.3 м. На рис. 1 представлены результаты 2013 года. Для сопровождения экспериментов использовалась акустическая метеостанция «Метео-2», которая располагалась на высоте 1.84 м на расстоянии 26 м от оси оптической трассы ДИТ по горизонтали и на 24 м от излучателя ДИТ в направлении распространения оптического излучения. Для сравнения с оптическими измерениями проводилась оценка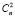 
из метеорологических измерений. Методика и аппаратура были аналогичны тем, которые описаны в статье [5]. Значения 
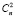оценивались по 60-и секундной реализации и выдавались с интервалом 60 секунд.
В период июля-августа 2014 года на обсерватории БЭК ИОА СО РАН были продолжены сопоставительные измерения: использованы следующие оптические измерители: ДИТ и оценка уровня турбулентности на основе использования динамических изображений. В измерениях на БЭКе также использовали акустический анемометр Метео-2. Измеренные значения Cn2 различными измерителями приведены на рис. 2: при этом акустический анемометр Метео-2 измерял постоянно, два оптических метода давали значения, усредненные за временную серию длиной 10 мин. Анализ результатов одновременных измерений показал, что значения структурной постоянной показателя преломления, вычисленные из оптических измерений ДВФ и ДИТ, отличаются незначительно (рис. 1, 2). В то же время при сравнении результатов трассовых оптических измерений и локальных измерений ультразвуковыми метеостанциями наблюдается подобие временных изменений структурной постоянной показателя преломления. Однако оценки уровня турбулентности из оптических измерений в большинстве случаев выше, чем из акустических измерений метеостанциями.
На наш взгляд, это может быть связано с неучетом влияния конечности величины внутреннего масштаба турбулентности. Известно [1, 4], что структурная функция температуры в атмосфере описывается (для модели Колмогорова-Обухова) степенной функцией следующего вида:
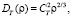
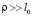. (7)
Если же учесть влияние внутреннего масштаба l0, то для разносов точек наблюдения ρ ≤ l0, имеет место квадратичный рост, т.е.
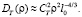(8)
В свое время [1] Гурвич А.С. предложил очень полезную модель, описывающую одновременно оба этих участка поведения структурной функции температуры атмосферы, а именно
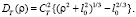(9)
Далее воспользуется этой моделью для описания экспериментальной функции флуктуаций температуры DT(ρ). Как известно, акустическая метеостанция определяет уровень структурного параметра температуры из данных временных измерений DT(ρ). В предположении «замороженности» атмосферной турбулентности, величина смещения точек наблюдения ρ определяется величиной поперечной скорости ветра v, обуславливающей смещение турбулентных неоднородностей, и всегда кратна частоте взятия отсчетов f акустической метеостанцией. Таким образом, минимальное пространственное смещение составляет ρmin = v/f. Предлагаем оценивать возможную величину коэффициента, связывающего значения структурного параметра температуры, вычисляемого по данным акустических измерений в пренебрежении влияния внутреннего масштаба турбулентности (т.е. при использовании формулы (7)) и при учете такого влияния – по формуле (9), на основе существования следующей связи между ними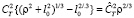 
, что дает
.
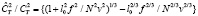Здесь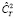 
представляет собой оценку структурного параметра, полученную в предположении, что имеет место чисто колмогоровский закон поведения структурной функции температуры, численный параметр N определяет величину разноса (смещения) между точками наблюдения, а именно ρ = Nρmin = vN/f.
Далее возьмем в качестве параметра величину l0 f/Nv и просчитаем отношение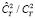 
для различных значений этого параметра, результаты представим в виде таблицы.
Рис. 1. Временные изменения структурной постоянной показателя преломления (данные 2013 года)
Рис. 2. Одновременные измерения структурной постоянной показателя преломления воздуха двумя оптическими методами и акустическим методом (данные 2014 года)
|
|
0 |
0.05 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.7 |
1 |
2 |
|
|
1 |
0.86 |
0.78 |
0.67 |
0.56 |
0.50 |
0.45 |
0.35 |
0.25 |
0.12 |
Из ее анализа получаем, что в результате неучета конечности величины внутреннего масштаба турбулентности возможно только занижение данных измеренного уровня турбулентности. Ошибка занижения измеренного значения уровня турбулентности акустическим измерителем (т.е. отношение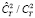 
) при реальных значениях внутреннего масштаба, реализуемых в атмосфере, может составлять 1.4–4 раза, причем она зависит, как от величины внутреннего масштаба турбулентности, так и от величины скорости ветра и частоты снятия отсчетов. Это заставляет уделять более пристальное внимание оценке величины внутреннего масштаба турбулентности при проводимых измерениях. Это можно делать, либо на основе проведения дополнительных градиентных измерений температуры и скорости ветра [3], либо из анализа поведения всей структурной функции температуры [11]. При этом величину внутреннего масштаба турбулентности можно получить из данных пересечения двух асимптотик (7) и (8). Интересно отметить, что (по данным таблицы) более подверженными влиянию внутреннего масштаба турбулентности оказываются акустические измерители, работающие на более высоких частотах снятия отсчетов.
Следует заметить, что модель Гурвича А.С. (9) конечно не может абсолютно правильно описывать реальные структурные функции, получаемые в экспериментах, однако она, в целом, позволяет указать возможные величины искажений измеряемых значений уровня турбулентности. А в практических случаях данные измерений структурной функции температуры, прежде чем проводить оценку величины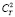 
, необходимо приводить к эффективной степенной модели вида (7). Следует также отметить, что данные акустического зондирования фактически дают возможность оценки величины 
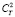и также опосредовано величины
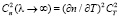. Для правильно перехода к оптическим данным необходимо также учитывать спектральную зависимость структурной постоянной показателя преломления атмосферы от длины волны излучения, которая в диапазоне от 0.2 мкм до 20 мкм достаточно хорошо аппроксимируется в условиях низкой влажности зависимостью вида
.
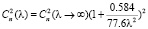В работе [11] уже были исследованы некоторые аспекты зависимости угловых оптических измерений в атмосфере от спектрального состава используемого излучения. Так, например, для длины волны 0.66 мкм множитель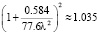 
, поэтому данные, получаемые из акустических измерений необходимо умножить на этот числовой множитель, что увеличивает измеренные с помощью акустических датчиков примерно на 3.5 %.
Поведение структурной функции флуктуация фазы в турбулентной среде
Попробуем рассчитать, какой вид будет иметь корреляционная функция флуктуаций фазы для модели атмосферной турбулентности следующего вида:
.
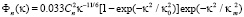Эту модель успешно использовали для расчетов флуктуаций оптических волн, ввиду простоты используемых расчетов. Рассчитаем поведение корреляционной функции флуктуаций фазы в плоской волне, тогда
.
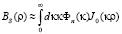Нетрудно показать, что ключевым здесь является интеграл вида
.
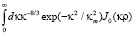Это в результате, при условии, что κ0 <<κm дает:
.
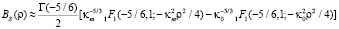Известно, что в этих условиях дисперсия флуктуаций фазы
.
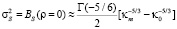Выполнив нормировку, получаем для нормированной корреляционной функции
.
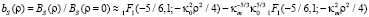Нетрудно показать, что если радиус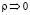 
, тогда 
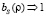. Наиболее интересен случай, когда 
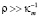, но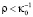 
, тогда
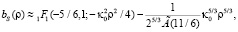
а в пределе (когда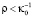 
) имеем, что bs(ρ) ≈ 1 – (ρκ0)5/3.
Это означает, что в этой области масштаб корреляции флуктуаций фазы будет представлять собой практически внешний масштабам турбулентности. Еще раз вернемся к поведению нормированной корреляционной функции флуктуаций фазы в области, когда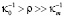 
, имеем
.
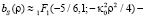
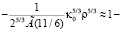
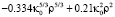Как показывают численные оценки налицо затянутый характер спада корреляции в области разносов точек наблюдения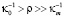 
.
Безусловно, эти моменты следует учитывать, особенно при расчете применения [12–14] адаптивных систем в атмосфере.