Введение
Возможности формирования структурированного пространства путем разбиения его на модулярные ячейки и моделирования невырожденных модулярных структур проанализированы в [1-3]. Получены вероятные представления гиперполиэдров в 3D пространстве и модулярные ячейки структур из правильных и полуправильных политопов 4D пространства [4-8]. Проанализированы гомологические соотношения и топологические преобразования возможных модулярных гиперячеек [9,10], а в работах [11-14] приведены вероятные механизмы проявления кубической Р-ячейки 4D пространства в ячеистых пространствах меньшей мерности.
Дана общая характеристика возможных гибридных фрактальных структур и сформулированы принципы их формирования [15-17]. В [18-23] приведены примеры формирования детерминистических фрактальных структур в 2D пространстве. Некоторые из полученных фрактальных структур в [24] рассматривались как возможные абстракции сайз-распределения фаз и конфигурации межфазных границ на поверхности композиционных материалов.
Проведена классификация возможных структурных состояний детерминистических модулярных структур с кристаллической, фрактальной и наноразмерной компонентами в 2D и 3D пространствах [25-28]. Сформулированы принципы их формирования [29, 30]. Получены и определены размерные характеристики возможных многокомпонентных структурных состояний системы [31-38]. Установлено вероятное влияние условного размерного параметра на чувствительные к особенностям структурной организации свойства систем [39, 40].
Проанализируем влияние мерности пространства d и размерного параметра объекта D на некоторое его аддитивное свойство S.
Вывод зависимости аддитивного свойства комплексного объекта от его размерности
В данной работе будем считать, что характер влияния для i-го структурного состояния определяется зависимостями типа Si(d/Di). В этом случае на свойство SD влияет отношение мерности пространства d и условного размерного параметра D, т.е. (d/D):
SD = Sd KD (d/D),
где KD – коэффициент пропорциональности, зависящий от величины отклонения условного размерного параметра состояния от мерности пространства, в котором определена структура R. Условный размерный параметр D для каждого структурного состояния может быть рассчитан следующим образом:
D = dr D(r) + df D(f) + dn D(n),
где dr, df и dn – количества соответствующих компонент одного сорта, для кристаллической компоненты D(r) = 1, для фрактальной компоненты он совпадает с фрактальной размерностью: D(f) = DimRf = Dim (GenRf) < 1, для наноразмерной компоненты D(n) = (<n>/no) < 1, если средний размер нанообъекта <n> < no = 100 нм.
Проанализируем вероятное влияние мерности d пространства, в котором определено структурное состояние комплексного объекта, на величину его аддитивного свойства.
Определим геометрию структурированного 4D пространства следующим образом:
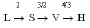 ,
,
где над морфизмами стоят показатели степени, возведение в которые есть соответствующий оператор перехода к большей мерности пространства.
Тогда матрица, столбцы которой представляют варианты обозначений «объемов» пространственных ячеек соответствующих подпространств 4D пространства:
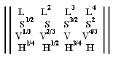
подразумевает наличие связей вида S = L2, L = S1/2; V = L3 = S3/2, L = V1/3; H = L4 = S2 = V4/3, L = H1/4 и т.д.
Рассмотрим аддитивное свойство m комплексного объекта.
Случай 1 – неоднородное пространство. В зависимости от мерности подпространств 4D пространства взаимосвязи между его соответствующими подсвойствами определим следующим образом:
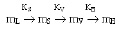 ,
,
где над морфизмами стоят коэффициенты перехода к этому же свойству объекта в пространстве с более высокой мерностью.
Соответствующая матрица возможных взаимосвязей между подсвойствами свойства m:
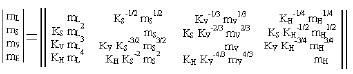
Тогда соответствующая матрица соотношений между свойствами объекта в подпространствах с близкой мерностью выглядит следующим образом:
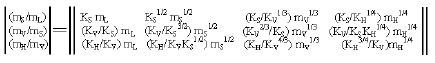
или
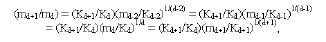
откуда имеем
md+1 = Kd+1 (md/Kd)(d+1)/d или
md = Kd (md+1/Kd+1)d/(d+1).
Тогда одновременное влияние мерности пространства d и размерности объекта D на некоторое его аддитивное свойство S с учетом равенства Sd = md может быть представлено следующим образом:
SD, d = Kd (md+1/Kd+1)d/(d+1)KD(d/D).
Случай 2 – однородное пространство. Если взаимосвязи между подсвойствами комплексного объекта в разных подпространствах определим одинаковым образом: KS = KV = KH = KL, то соотношения между свойствами в подпространствах с близкой мерностью
(md+1/md) = (KL md-2)1/(d-1) = (KL md-1)1/d =
=(KL md)1/(d+1) =(KL md+1)1/(d+2),
откуда имеем
md+1 = KL1/(d+1) md(d+2)/(d+1) или
md = KL-1/(d+2) md+1(d+1)/(d+2).
Тогда влияние мерности пространства d и размерного параметра объекта D на некоторое его аддитивное свойство S с учетом равенства Sd = md может быть представлено следующим образом:
SD, d = KL-1/(d+2) md+1(d+1)/(d+2) KD(d/D).
Таким образом, одновременное влияние мерности пространства d и размерности объекта D на некоторое его аддитивное свойство S может быть представлено в зависимости от степени однородности пространства двумя простыми линейными зависимостями.
Выводы
Получены возможные простые зависимости аддитивного свойства некоторого комплексного объекта от его размерного параметра D и мерности d неоднородного или однородного пространства, в котором реализуется его структурное состояние, включающее кроме кристаллической также наноразмерную и фрактальную компоненты. Отметим, что возможное влияние размерных параметров состояния поверхности, обусловленных кристаллическими фазами, наночастицами или квазифрактальными конфигурациями межфазных границ, на трибологические свойства поверхности композиционных материалов и покрытий на основе систем Ni-P и Ni-B были использованы в [41–51].



