Процесс обучения как сложный динамический процесс, в результате которого также происходит изменение объекта этого процесса (в данном случае – обучающихся), обладает общими и характерными свойствами, присущими многим системам, как в живой, так и в неживой природе [1]. Это обстоятельство дает возможность разработать модель учебного процесса с точки зрения неравновесной статистической термодинамики. Отметим, что рассматриваемый подход несколько отличается от синергетического подхода. Синергетика – это термодинамика открытых систем. Хотя педагогическая система, вообще говоря, представляет собой открытую систему, однако для получения конкретных количественных результатов обучение замыкается в некоторой актуальной достаточно ограниченной среде. Эту актуальную окружающую среду будем представлять «термостатом».
Рассмотрим группу обучающихся (студентов). Будем считать, что реализован индивидуальный подход к процессу обучения и студенты представляют собой невзаимодействующие объекты. Кстати, это вполне соответствует современной тенденции, например, электронному обучению с личным кабинетом. Среда обучения, которая моделируется «термостатом» с невзаимодействующими объектами фактически представляет собой некоторый «черный ящик», взаимодействие с которым приводит к диссипативным процессам, т.е. к потере части переданной учебной информации, с некоторой вероятностью Р. Внешним полем служит преподаватель, передающий определенный объем информации группе студентов. Переход подсистемы обучения (группы студентов) за счет взаимодействия с преподавателем в новое состояние осуществляется с вероятностью F.
При принятых допущениях подсистема обучения представляет собой канонический ансамбль. Рассматривая вероятность диссипативных процессов, воспользуемся формулой для термодинамических процессов
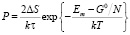, (1)
где ΔS – изменение энтропии в диссипативном процессе;
Em – среднее значение «информационной емкости» группы студентов;
τ – время диссипативного процесса.
Отклик подсистемы студентов или эффективность усвоения переданной информации предлагается оценивать следующим образом:
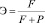, (2)
где F – вероятность передачи учебной информации, причем F = 1/τp;
τp – время передачи учебной информации.
Тогда, с учетом (2), имеем:
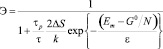. (3)
Оценка эффективности усвоения учебного материала и повышение этой эффективности, очевидно, является важнейшим вопросом практической педагогики [5]. Для оценки эффективности напрямую нужно измерять накопленные знания, что связано с необходимостью проведения большого числа массовых педагогических экспериментов. В педагогике эксперимент, конечно чрезвычайно важен. В то же время проведение многих экспериментов связано с целым рядом трудностей. Прежде всего, в педагогике правомерен отнюдь не любой эксперимент. Кроме того, сам эксперимент и проявление его результатов, как правило, разнесены во времени. Другая сложность – это «воспроизводимость» результатов педагогического эксперимента. Это связано с тем, что проведение эксперимента может так изменить состояние объектов, что вернуть их в первоначальное состояние для повторного эксперимента окажется невозможным. Указанные трудности указывают на важность создания моделей, позволяющих изучать педагогические явления. С учетом этого предложенная оценка эффективности усвоения учебного материала студентами по формуле (3) представляется интересной. Формулу (3) можно преобразовать следующим образом:
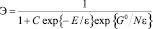, (4)
где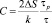 
. Разлагая экспоненты в знаменателе в ряд и пренебрегая малыми членами, в линейном приближении можно получить следующую оценку:
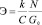. (5)
Можно предположить, что аналог энергии Гиббса – аддитивная величина, которая равна
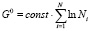. (6)
Полагая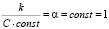 
, с учетом (6) и 
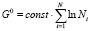, из (5), получается:
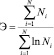. (7)
Уравнение (7) показывает зависимость усвоения учебного материала студентами от количества последних. Подобный эффект связан с наличием в группе студентов из N – человек диссипативного канала потери информации. График функции (7) представлен на рис. 1.
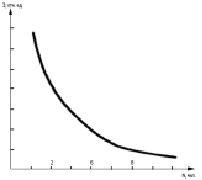
Рис. 1. Эффективность усвоения учебного материала как функция числа студентов
Из рис. 1 следует, что эффективность усвоения учебного материала максимальна, когда в группе всего 1 человек, что вполне объяснимо. С учетом изгиба кривой видно, что эффективное освоение материала возможно в группах не более 6 студентов.
Из приведенной модели можно сделать два вывода:
– во-первых, для увеличения эффективности усвоения учебного материала желательно сокращать число студентов в группе;
– во-вторых, для повышения эффективности обучения в больших группах необходимо организовать взаимодействие студентов.
Действительно, рассмотренная модель группы студентов, предполагала отсутствие взаимодействия в группе. Наличие активного взаимодействия, например, методы проектного обучения значительно повышает эффективность за счет совместной познавательной деятельности.
Рассмотрим теперь зависимость эффективности усвоения учебного материала от накопленного фонда информации. Теории, сосредоточенные на роли знания и его организации, часто подчеркивают роль накопленной информации в долгосрочной памяти как ключ к пониманию компетентности. Эти теории исходят из работ де Грота [2].
Де Грот, как известно, проводил эксперименты с шахматистами и пришел к выводу, что приобретенные посредством опыта знания, а не какой-либо другой вид обработки информации и являются тем, что отличает гроссмейстера от обычных шахматистов. Чейз и Саймон предположили, что у гроссмейстеров память лучше, чем у обычных игроков. Они проверили эту гипотезу и оказалось, что уровень компетентности влияет на запоминание только стратегически важных шахматных комбинаций из реальных игр. Иными словами, специалиста от новичка, гроссмейстера от обычного шахматиста отличает не способность сохранять информацию в памяти, а уровень их базы знаний и ее организация. Эта организация может быть в виде проблемной схемы – костяка знаний, на который можно опереться, чтобы лучше представить проблему и затем решить ее. Столь значимое открытие, касающееся роли базы знаний, может быть применено к большинству организованных компетенций. Таким образом, обширная и организованная база знаний и возникающие вместе с ней проблемные схемы представляются фундаментально важными для разнообразных видов компетентности.
В рамках рассматриваемой нами модели параметром, характеризующим накопленный фонд информации, является Em. Полагая, что Э = F/P, и используя формулы (1) и (2) при постоянных прочих условиях, получается:
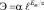, (8)
где α, ε = const.
Из (8) следует, что зависимость эффективности усвоения материала от первоначального фонда информации значительно сильнее, чем простая пропорциональность, отмеченная упомянутыми выше исследователями. График зависимости (8) схематично приведен на рис. 2.
Из полученной закономерности можно сделать вывод о том, что прежде, чем начинать преподавание нового курса, необходимо с помощью хорошо составленных тестов выявить базовый фонд информации, имеющийся у студента для усвоения данного предмета. Если параметр Em мал, то необходимы вводные лекции, на которых создаются предпосылки для дальнейшего усвоения материала новой дисциплины. Решающее значение в резком увеличении базового фонда информации играет овладение студентом, особенно на первом курсе, техникой быстрой обработки информации (чтения и мышления). Весьма важной при этом является оценка интеллектуальных способностей студента. Интеллектуальные способности можно оценивать качеством (глубиной) знаний. Изучению качества знаний посвящено немало исследований. Основой изучения знаний, их глубины является деятельностный подход, развитый в фундаментальных работах Л.С. Выготского, С.Л. Рубинштейна, А.Н. Леонтьева [1, 3, 4]. В качестве единицы психологического анализа рассматривается действие, которое исходит из определенных мотивов и направлено на выполнение конкретной цели. При этом оно выступает как заключительный акт учебной деятельности. Изменение условий при сохранении цели действия ведет к изменению ее операционной части. Если действие выполняется в различных условиях, то оно обобщается, выступая как умение. Таким образом, в психологическом плане умение является мерой обобщения и освоения действия.
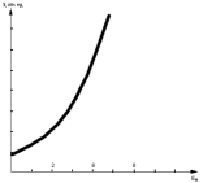
Рис. 2. Зависимость эффективности усвоения от объема первичной информации
Можно сделать два вывода, имеющие практическое значение:
1) умение – это обобщенное действие, которое может быть выполнено обучаемым в различных конкретных условиях; оно выступает как результат обобщения и освоения действия;
2) глубина знаний характеризует уровень соответствующего умения.
Имеющиеся результаты по изучению процесса формирования умения как обобщенного действия позволяют выделить, по крайней мере, три важные стороны. Например, при решении математических задач на дифференцирование функции студент может осознавать, как выполняется действие, т.е. осознавать, какие операции и в какой последовательности следует произвести на этапе дифференцирования функции, но не уметь операционно выполнить действие в данной конкретной ситуации.
В этом случае у студента сформирована лишь ориентировочная основа обобщенного действия – умение дифференцировать. С другой стороны, студент может выполнить операционную часть данной задачи, т.е. он осознает, как следует выполнить действие, но не осознает его в теоретическом плане, а именно, на уровне его ориентировочной основы. И, наконец, возможна третья ситуация. Как показывают исследования по формированию умения, студент может владеть действием на первых двух уровнях, т.е. уметь сконструировать и выполнить задачу, не осознавая при этом процесс получения результата и способа его проверки. Из сказанного выше следует, что определение «глубины знаний» или интеллекта представляет собой непростую задачу.
Для решения вопроса о практической оценке уровня интеллекта (глубины знаний) в рамках рассматриваемой модели предлагается использовать параметр Em:
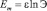, (9)
где Э – эффективность (скорость) усвоения учебного материала; ε – параметр, характеризующий интеллектуальный уровень обучаемого.
График этой зависимости Em показан на рис. 3. Из рисунка видно, что уровень интеллекта при обучении имеет насыщение и дальнейшее его увеличение невозможно. Это обусловлено ограниченностью параметра Э.
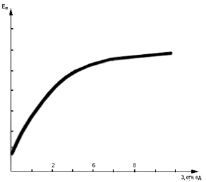
Рис. 3. Зависимость глубины знаний от эффективности усвоения
В заключение отметим, что использование формулы (9) для оценки интеллекта было бы намного эффективнее, если бы мы имели некоторый «эталон интеллекта». Однако общепринятого эталона пока не существует.