Вода, используемая живыми организмами, а также человеком – это обычная вода (H2O). Тяжелая (D2O) и сверхтяжелая (T2O) воды вредны для живых организмов. Тяжелая вода замедляет биологические процессы и губительно действует на живую клетку. Различие в физико-химических свойствах различных вод, по-видимому, связано с их структурой.
Целью данной работы является сравнение структуры этих вод (H2O, D2O, T2O). С этой целью на основе данных (таблица [2, 5, 6, 7, 8, 10]) динамической вязкости и плотности обычной (H2O), тяжелой (D2O), и сверхтяжелой (T2O) воды в интервале температур 273,15–373,15 K определены энергия активации Гиббса вязкого течения (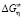 ), энергия активации энтальпии вязкого течения (
), энергия активации энтальпии вязкого течения (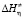 ), энергия активации энтропии вязкого течения (
), энергия активации энтропии вязкого течения (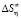 ), и на основе сравнения этих параметров при данной температуре проанализированы структурные особенности каждой воды.
), и на основе сравнения этих параметров при данной температуре проанализированы структурные особенности каждой воды.
Материалы и методы исследования
Объекты исследования. Объектами исследования являлись вода (H2O), тяжелая вода (D2O) и сверхтяжелая вода (T2O) при различных температурах.
Температурная зависимость динамической вязкости и плотности обычной (H2O), тяжелой (D2O), и сверхтяжелой (T2O) воды в интервале температур 273,15 – 373,15 K дана в таблице [2, 5, 6, 7, 8, 10].
Из таблицы [2, 5, 6, 7, 8, 10] видно, что при данной температуре значения динамической вязкости и плотности тяжелой воды (D2O) больше обычной (H2O), а сверхтяжелой воды (T2O) больше тяжелой (D2O).
Результаты исследования и их обсуждение
Активационные параметры вязкого течения (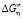 ,
, 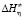 ,
, 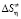 ) вычислены следующим образом:
) вычислены следующим образом:
а) вычисление энергии активации Гиббса (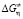 ) вязкого течения.
) вязкого течения.
Динамическая вязкость и плотность при разных температурах и при нормальном атмосферном давлении для обычной воды (H2O), тяжелой воды (D2O) и сверхтяжелой воды (T2O)
|
T, K |
η, мПа∙с |
ρ, кг/м3 |
||||
|
H2O |
D2O |
T2O |
H2O |
D2O |
T2O |
|
|
273,15 |
1,7921 |
2,4000 |
2,770 |
999,843 |
1104,62 |
1212,5 |
|
278,15 |
1,5193 |
1,9880 |
2,270 |
999,967 |
1105,58 |
1214,2 |
|
283,15 |
1,3073 |
1,6790 |
1,900 |
999,703 |
1105,95 |
1214,8 |
|
288,15 |
1,1383 |
1,4400 |
1,620 |
999,103 |
1105,83 |
1215,0 |
|
293,15 |
1,0020 |
1,2510 |
1,400 |
998,207 |
1105,34 |
1214,6 |
|
298,15 |
0,8902 |
1,1000 |
1,220 |
997,048 |
1104,48 |
1213,7 |
|
303,15 |
0,7973 |
0,9759 |
1,080 |
995,650 |
1103,27 |
1212,5 |
|
308,15 |
0,7191 |
0,8733 |
0,957 |
994,035 |
1101,69 |
1210,9 |
|
313,15 |
0,6527 |
0,7872 |
0,859 |
992,219 |
1099,99 |
1209,0 |
|
318,15 |
0,5961 |
0,7143 |
0,776 |
990,216 |
1097,94 |
1206,8 |
|
323,15 |
0,5471 |
0,6519 |
0,706 |
988,039 |
1095,65 |
1204,4 |
|
328,15 |
0,5044 |
0,5981 |
0,645 |
985,698 |
1093,14 |
1201,8 |
|
333,15 |
0,4670 |
0,5513 |
0,592 |
983,202 |
1090,51 |
1198,8 |
|
338,15 |
0,4339 |
0,5104 |
0,547 |
980,558 |
1087,67 |
1195,5 |
|
343,15 |
0,4046 |
0,4744 |
0,506 |
977,773 |
1084,72 |
1192,3 |
|
348,15 |
0,3785 |
0,4425 |
0,471 |
974,852 |
1081,43 |
1188,7 |
|
353,15 |
0,3551 |
0,4141 |
0,440 |
971,801 |
1078,17 |
1185,1 |
|
358,15 |
0,3341 |
0,3887 |
0,412 |
968,623 |
1074,69 |
1181,4 |
|
363,15 |
0,3150 |
0,3658 |
0,386 |
965,322 |
1071,01 |
1177,4 |
|
368,15 |
0,2978 |
0,3452 |
0,364 |
961,902 |
1067,24 |
1173,2 |
|
373,15 |
0,2821 |
0,3266 |
0,343 |
958,365 |
1063,38 |
1169,0 |
На основе теории Эйринга [1] динамическая вязкость (η) определяется следующим образом:
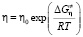 , (1)
, (1)
где
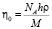 . (2)
. (2)
В выражениях (1) и (2) ρ – плотность жидкости, R – универсальная газовая постоянная, NA – число Авогадро, h – постоянная Планка, M – молярная масса жидкости. По экспериментально определенным зависимостям η и ρ от температуры, используя выражение
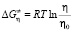 , (3)
, (3)
находили температурную зависимость свободной энергии Гиббса;
б) вычисление энтальпии активации (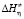 ) вязкого течения.
) вязкого течения.
Учитывая выражение (3) в термодинамическом соотношении
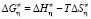 , (4)
, (4)
получим [4]
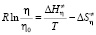 . (5)
. (5)
Отметим, что параметры 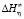 və
və 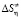 также зависят от температуры. Однако для бесконечно малого температурного интервала эти параметры можно считать постоянными и, взяв частную производную по
также зависят от температуры. Однако для бесконечно малого температурного интервала эти параметры можно считать постоянными и, взяв частную производную по 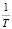 с обеих сторон выражения (5), получим
с обеих сторон выражения (5), получим
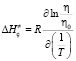 . (6)
. (6)
Частное производное 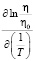 , входящее в уравнение (6), это число. Для нахождения значения этого числа при разных температурах строится зависимость
, входящее в уравнение (6), это число. Для нахождения значения этого числа при разных температурах строится зависимость 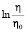 от
от 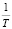 . Затем полученная кривая описывается функцией вида:
. Затем полученная кривая описывается функцией вида:
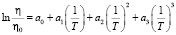 . (7)
. (7)
Здесь а0, а1, а2 и а3 – независимые от температуры параметры, и их значения определяются методом математической оптимизации. С учетом (7) в выражении (6), получим выражение для определения температурной зависимости 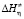 :
:
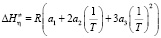 ; (8)
; (8)
в) вычисление энтропии активации (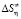 ) вязкого течения.
) вязкого течения.
После нахождения температурных зависимостей 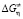 и
и 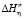 из формулы (4) находится выражение для определения температурной зависимости энтропии активации вязкого течения [4]:
из формулы (4) находится выражение для определения температурной зависимости энтропии активации вязкого течения [4]:
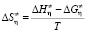 . (9)
. (9)
Отметим, что активационные параметры, характеризующие процесс вязкого течения представляют собой разность соответствующих термодинамических параметров активного (Ga, Ha, Sa) и начального (Gн, Hн, Sн) состояний молекул одного моля жидкости [9]:
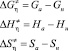 . (10)
. (10)
Следует отметить, что энергия активации Гиббса (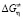 ) вязкого течения – это энергия, требуемая для перехода 1 моля молекул жидкости из начального состояния в текучее состояние при данных давлении и температуре. Энтальпия активации (
) вязкого течения – это энергия, требуемая для перехода 1 моля молекул жидкости из начального состояния в текучее состояние при данных давлении и температуре. Энтальпия активации (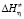 ) вязкого течения является энергетической характеристикой изменений в растворе [3, 9]. Так, увеличение значения
) вязкого течения является энергетической характеристикой изменений в растворе [3, 9]. Так, увеличение значения 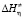 означает переход системы в более структурированное состояние. Энтропия активации вязкого течения (
означает переход системы в более структурированное состояние. Энтропия активации вязкого течения (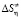 ) характеризует структурные изменения, происходящие в жидкости. Чем больше структурированной будет начальное состояние жидкости, тем меньше станет энтропия начального состояния (Sн) и тем больше будет ее изменение (Sа – Sн) при течении и наоборот. Следовательно, для рассматриваемой системы большему значению
) характеризует структурные изменения, происходящие в жидкости. Чем больше структурированной будет начальное состояние жидкости, тем меньше станет энтропия начального состояния (Sн) и тем больше будет ее изменение (Sа – Sн) при течении и наоборот. Следовательно, для рассматриваемой системы большему значению 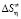 соответствует более структурированное состояние системы [9].
соответствует более структурированное состояние системы [9].
Температурные зависимости активационных параметров вязкого течения (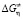 ,
, 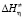 ,
, 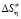 ) для обычной (H2O), тяжелой (D2O) и сверхтяжелой (T2O) воды представлены на рисунке.
) для обычной (H2O), тяжелой (D2O) и сверхтяжелой (T2O) воды представлены на рисунке.
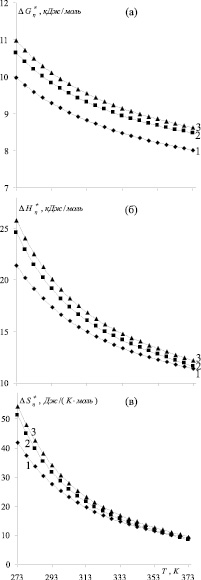
Температурная зависимость свободной энергии Гиббса (а), энтальпии (б) и энтропии (в) активации вязкого течения. 1 – H2O, 2 – D2O, 3 – T2O
Как видно из рисунков, параметры 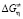 ,
, 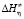 и
и 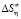 с увеличением температуры уменьшаются. При этом для произвольной температуры справедливо нижеследующее:
с увеличением температуры уменьшаются. При этом для произвольной температуры справедливо нижеследующее:
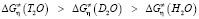
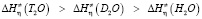
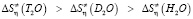 .
.
Эти соотношения позволяют сделать вывод о том, что при данной температуре тяжелая вода относительно обычной, а сверхтяжелая вода относительно тяжелой является более структурированной.




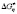 ), enthalpy of viscous flow (
), enthalpy of viscous flow (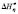 ) and activation parameters of entropy of viscous flow (
) and activation parameters of entropy of viscous flow (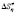 ) at normal atmospheric pressure and in the temperature range 273,15–373,15 K. These calculations were made for different values of the dynamic viscosity and density. It has been found that when increasing the temperature the values of Gibbs free energy
) at normal atmospheric pressure and in the temperature range 273,15–373,15 K. These calculations were made for different values of the dynamic viscosity and density. It has been found that when increasing the temperature the values of Gibbs free energy 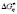 , enthalpy
, enthalpy 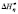 and entropy
and entropy 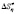 are tend to reduce, however, at any chosen temperature the following relationship between those parameters were observed
are tend to reduce, however, at any chosen temperature the following relationship between those parameters were observed 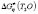 >
> 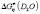 >
> 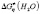 ,
, 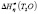 >
> 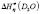 >
> 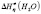 ,
, 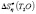 >
> 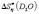 >
> 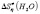 . This allows to come to the following conclusion that at the given temperature heavy water becomes more structured in comparison with conventional water, and tritiated water becomes more structured in comparison with heavy water.
. This allows to come to the following conclusion that at the given temperature heavy water becomes more structured in comparison with conventional water, and tritiated water becomes more structured in comparison with heavy water.