Одной из главных эвристических задач естественных наук является разработка новых методов прогнозирования [3]. Для решения этой задачи можно использовать два подхода: индуктивный и дедуктивный.
При индуктивном подходе исходят из некоторой совокупности полуэмпирических методик прогнозирования определенного класса веществ. Результат последовательного обобщения этих методик может привести в конечном итоге к методу прогнозирования веществ.
Дедуктивный подход предполагает возможность существования некоторых начальных положений, использование которых приводит к построению некоторого «суперметода» прогнозирования, на основе которого возможно формулирование метода или системы методов прогнозирования веществ.
Очевидно, что во втором подходе достигается большая степень эвристичности результатов. Основные этапы реализации дедуктивного подхода к разработке методов прогнозирования:
1) анализ существующих абстрактных математических конструкций (структур математических теорий), которые обеспечат выполнение требований полноты, аддитивности, эволюционности и оптимальной абстрактности, предъявляемых к прогнозной модели М, и могут быть заложены в основу необходимых концептуальных построений;
2) анализ теоретических концептуальных построений (концептуальных конструктов) для получения концептуальных систем в соответствующих отраслях естественно-научного знания;
3) вывод возможных концептуальных систем путем преобразования представления о концептуальном конструкте;
4) анализ возможных стратегий прогнозирования, функционально адекватных суперметодам, путем интерпретации используемой концептуальной системы;
5) формулирование задач прогнозирования, решение которых приводит к реализации соответствующей стратегии;
6) разработка метода прогнозирования или системы методов.
Проанализируем возможности дедуктивного подхода при разработке методических основ идеологии прогнозирования, получения возможных вариантов концептуальных систем и стратегий прогнозирования неорганических веществ.
Методическая основа идеологии прогнозирования материальных объектов
На основе анализа результатов предпрогнозной ориентации об объекте прогнозирования (О) может быть получена информация в виде его деформированного изображения (Iдеф). Интерпретация этого изображения объекта и переход к самому объекту прогнозирования осуществляется по-разному. Соотношение между объектом О, его образом Р, моделью М и различными видами изображений (идеальным Iид и аппроксимированным Iаппр) представлены на рисунке.
Для решения задач прогнозирования объектов неорганической природы могут быть использованы методы теории образов. Реализация этих методов основана на проведении следующих процедур и соответствующих им переходов:
1) восстановление изображения: Iдеф → Iид;
2) аппроксимация изображения: Iдеф → Iаппр;
3) анализ изображения и его описание: Iдеф → I;
4) распознавание образа: Iдеф → P;
5) классификация образа: (Iаппр, Iид) → P;
6) вывод (абдукция) образа: I → P;
7) моделирование объекта: (P, I) → M;
8) объяснение и идентификация объекта: (Iид, Iаппр, I, M) → O.
Формально все эти процедуры могут быть использованы для решения прогнозных задач по следующим частным стратегиям:
1) Iдеф → Iид ⇒ О,
2) Iдеф →Iаппр ⇒ О,
3) Iдеф → I ⇒ О,
4) Iдеф →Iаппр → Iид ⇒ О,
5) Iдеф → Iид→ I ⇒ О,
6) Iдеф → I → М ⇒ О,
7) Iдеф →Iаппр → I → М⇒ О,
8) Iдеф → Р → М ⇒ О,
9) Iдеф → I → Р → М ⇒ О,
10) Iдеф → Iид → I → Р → М ⇒ О,
11) Iдеф →Iаппр → Р → М ⇒ О.
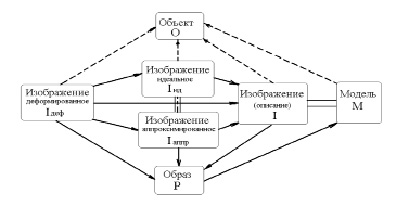
Схема соотношений между Объектом, его различными Изображениями, Моделью и Образом
Отметим, что процедура, описывающая переход Iдеф → P методом распознавания образов, по своей структуре реализации адекватна процедуре прогнозирования материальных объектов. По-видимому, информация об объекте, полученная с помощью процедуры распознавания образа и последующим его моделированием, будет наиболее достоверной. Данная процедура присутствует в стратегиях 8–11, из которых восьмая является самой простой.
Таким образом, методы теории образов могут послужить методической основой для создания идеологии прогнозирования материальных объектов, в том числе и неорганических веществ.
Возможные варианты концептуальной системы структурных теорий химии
В основе любой абстрактной структуры математических теорий лежит одно или несколько отношений, в которых находятся элементы некоторого множества. Эти отношения могут быть композиционными (алгебраические структуры), порядковыми (структуры порядка), топологическими (топологические структуры), либо комбинациями перечисленных выше вариантов отношений (алгебраические или топологические структуры порядка, тополого-алгебраические структуры и тополого-алгебраические структуры порядка). Рассмотрение каждого из видов структур приводит к соответствующим концептуальным построениям (концептуальным конструктам):
1. Элемент – Состав – Структура (1).
2. Элемент – Порядок – Структура (2).
3. Элемент – Топология – Структура (3).
4. Элемент – Состав, Порядок – Структура (4).
5. Элемент – Состав, Топология – Структура (5).
6. Элемент – Порядок, Топология – Структура (6).
7. Элемент – Состав, Порядок, Топология – Структура (7).
Структуры (1)–(7) отличаются по содержанию. Только в первом концептуальном конструкте Структура является полностью композиционно зависимой, а сам конструкт максимально соответствует второй концептуальной системе в химии – системе структурных теорий. Рассмотрим процедуру построения данного концептуального конструкта для целей прогнозирования и определим возможные его модификации, с которыми можно работать как с условными моделями.
Элементы. Будем рассматривать конечное или с мощностью некоторого континуума множество элементов Е = {ei}. Допустим, что для e1,e2∈E найдется отношение эквивалентности p∈P: pe1 = e2, которое обеспечит разбиение множества Е на классы подобных элементов Еa = {e|a (e) = a}∈Е, где a – фундаментальная характеристика, индекс класса. Допустим также, что элементы характеризуются числом связей w(e) и показателями связей b(e). Комбинаторная теория образов предусматривает структурное объединение элементов в конфигурации.
Конфигурации. Будем рассматривать множество конфигураций С = {cij}, где cij {ei, ej} – комбинация из элементов, связанных друг с другом связями с показателями bi(ei) и bj(ej). Конфигурации характеризуются отношением связей r (характеристиками допустимости соединения связей элементов ei и ej с показателями bi и bj) и типом соединения элементов r∈R (R – множество графов, описывающих способ соединения связей элементов друг с другом или структуру конфигурации). Допустим, что заданы комбинаторные правила P = , с помощью которых задается множество регулярных конфигураций или множество регулярных структур C(P). Для описания информационных потерь, вызванных ограничениями по наблюдаемости, необходим переход от конфигураций к изображениям.
Изображения. Допустим, что задано правило идентификации Id, которое интерпретирует регулярную структуру C(P) так, как она воспринимается наблюдателем. В этом случае для C1,C2∈C(P) символьная запись C1IdC2 означает C1 = C2, то есть конфигурации воспринимаются как эквивалентные, идентичные. Под изображениями I∈{Ii} будем понимать классы эквивалентности, индуцированные на множестве регулярных структур C(P) правилом идентификации Id. Множество {Ii} вместе с преобразованием подобия и комбинациями элементов посредством связей составляет алгебру изображений и может быть представлено следующим образом: A = . Здесь Е характеризует состав изображений а R – характеристика структуры комбинаций, составляющих изображение.
Образы и конструкты. Образ-представление об объекте может быть сконструирован на основе анализа некоторой совокупности его изображений, отличающихся несущественными деталями. Образ также характеризуется элементным составом и структурой конфигураций, его составляющих. Представление образа можно записать в виде условного конструкта К = , подразумевая, что элементы Е полностью определяют состав конфигураций С и их структуру R. В дальнейшем подобный концептуальный конструкт будем записывать в сокращенном виде как ЕСR.
Определим формально возможные модификации данного конструкта, основываясь на вероятных модельных изменениях представлений об объекте.
Механизмы преобразования конструктов. Образ-представление об объекте в виде концептуального конструкта ECR не учитывает его динамичность, многообразие связей между элементами, не отражает полноту системного подхода к анализу. В связи с этим предположим следующие механизмы его преобразования: эволюционный, гомологический и фуркационный.
Эволюционный механизм преобразования отражает возможность перехода объекта из одного состояния в другое и изменение отклика объекта на внешние воздействия в сравнении с другими объектами (т.е. изменение его свойства). В этом случае условный конструкт может быть представлен следующим образом: K = (или ECRUS), в котором дополнительные элементы U и S характеризуют возможные состояния объекта и свойства, непосредственно определяемые ими.
Гомологический механизм преобразования отражает системность анализа объекта. Каждая абстрактная конструкция может рассматриваться как элемент более сложной конструкции другого уровня организации, характеризующейся новым составом и структурой связей между новыми элементами. В то же время каждый элемент абстрактной конструкции при более детальном анализе может обнаружить сложное строение и рассматриваться как система элементов другого уровня. Отсюда следует, что рассматриваемый ранее одноуровневый конструкт K можно преобразовать в n-уровневый следующим образом: K(1) ⇒ K(n) или (ECRUS) ⇒ (…((ECRUS)(1) CRUS)(2) …CRUS)(n).
Фуркационный механизм преобразования основан на предположении о том, что для каждого класса элементов Ea = En эволюционного концептуального конструкта K(1) можно сформировать соответствующий конструкт частного порядка Kn. Тогда преобразование K(1) ⇒ Kn(1) отражается следующим образом: (ECRUS)(1) ⇒ (EEnCnRnUnSn)(1).
Направления прогнозирования неорганических веществ с заданными свойствами
Модифицированный вариант концептуальной системы структурных теорий химии и соответствующая ей матрица пятого ранга для коэффициентов разложения могут быть представлены следующим образом:
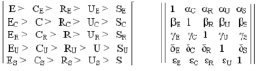
Формально возможны четыре основных направления моделирования (прогнозирования) неорганических кристаллов с заданными свойствами.
А. Моделирование химического состава веществ с заданным свойством. В предположении следующей матрицы для коэффициентов разложения

Стратегия прогнозирования диагностического свойства вещества выглядит так:
SC(UC(RC(C(EE)))).
Тогда состав представляет собой следующий образ:
C(EC) = CEαC (EC)*[CRγC(ER)*CUδC(EU)*CSεC(ES)]
В соответствии с концептуальной системой имеем следующие четыре варианта направления моделирования качественного и количественного состава вещества:
А-1. EC → C,
А-2. ER → CR → R → C,
А-3. EU → CU → RU → U → R → C,
А-4. ES → CS → RS → US → S → U → R → C.
Первая схема моделирования состава основана на использовании индивидуальных характеристик атомов: размеров, эффективных зарядов.
Реализация второй схемы моделирования основана на использовании структурных фрагментов. Состав фрагментов и их взаимное расположение в кристаллическом пространстве определяют количественные соотношения между атомами в формуле вещества и его кристаллическую структуру. Учет возможных кристаллохимических характеристик соответствующих компонентов может послужить способом получения информации о качественном составе вероятных соединений.
В основе реализации третьей схемы моделирования лежат результаты анализа возможного специфического состояния вещества. Выбор и тщательный анализ структурного элемента состояния позволяет получить необходимую информацию о возможном качественном составе и химической структуре предполагаемого фрагмента или некоторых фрагментов. Последующий анализ вероятного окружения этих гипотетических фрагментов в кристаллическом пространстве дает возможность определить симметрию кристалла и количественные показатели структурных характеристик. Определенная информация о качественном составе веществ может быть получена на основе кристаллохимического анализа возможных элементов состава, например, методом структурных полей (или карт).
Реализация последней схемы моделирования состава веществ основана на анализе их диагностического свойства. Основные этапы анализа:
1) выявление структурного фрагмента вещества – носителя диагностического свойства;
2) определение возможных вариантов количественного состава фрагмента;
3) определение собственной симметрии фрагмента и возможной симметрии его окружения;
4) определение характеристик специфического состояния, определяющего заданное свойство;
5) отбор наиболее вероятных вариантов реализации состояния;
6) определение симметрии кристаллической структуры из фрагментов;
7) кристаллохимический анализ и определение наиболее вероятных вариантов качественного состава вещества.
Б. Моделирование кристаллической структуры веществ с заданным свойством. Если форма матрицы коэффициентов разложения следующая:

то стратегия прогнозирования свойства вещества выглядит так: SR(UR (R(ER), C)). Тогда структура представляет собой следующий образ:
R(ER) = [REαR (ER)*RCβR (EC)]* *[RUδR (EU)*RSεR (ES)].
В этом случае имеем следующие варианты основных направлений моделирования структуры веществ:
Б-1. EC → C → RC → R,
Б-2. ER → CR → R,
Б-3. EU → CU → RU → U → R,
Б-4. ES → CS → RS → US → S → U → R.
Первая схема моделирования может быть реализована после определения химического состава вещества (пункт А-1). Молекулярная структура вещества рассматривается как результат проявления индивидуальных характеристик атомов в составе формульной единицы. Сравнительный анализ возможных вариантов размещений молекул или формульных единиц в кристаллическом пространстве позволяет получить информацию о соответствующих кристаллических структурах. Выбор наиболее вероятной структуры – последний этап реализации данной схемы моделирования.
Реализация второй, третьей и четвертой схем моделирования описана в пунктах А-2, А-3 и А-4 соответственно.
В. Моделирование специфического состояния кристаллических веществ, обуславливающего заданное свойство. Если форма матрицы коэффициентов разложения следующая:
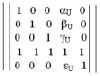
то стратегия прогнозирования соответствующего свойства SU(U(EU), RU, CU). В этом случае состояние представляет собой следующий образ:
U(EU) = [[UEαU (EU)*UCβU (EC)*URγU (ER)]* *USεU (ES)].
Основные варианты направлений моделирования состояния веществ:
В-1. EC → C → RC → R → U,
В-2. ER → CR → R → U,
В-3. EU → CU → RU → U,
В-4. ES → CS → RS → US → S → U.
Последние этапы первой и второй схем могут быть реализованы после структурного моделирования (пункты Б-1 и Б-2 соответственно). Процедуры определения характеристик специфического состояния могут рассматриваться как результат учета их корреляции с соответствующими структурными параметрами, определенными ранее.
Процедуры реализации третьей и четвертой схем моделирования описаны в пунктах Б-3 и Б-4 соответственно.
Г. Моделирование диагностического свойства кристаллических веществ. Если форма матрицы коэффициентов разложения следующая:
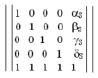
тогда стратегия прогнозирования соответствующего свойства S(ES, US, RS, CS). Cвойство может быть представлено следующим образом:
S(ES) = [SEαS (ES)*SCβS (EC)* *SRγS (ER)*SUδS (EU)].
Основные варианты направлений моделирования свойства веществ:
Г-1. EC → C → RC → R → U → S,
Г-2. ER → CR → R → U → S,
Г-3. EU → CU → RU → U → S,
Г-4. ES → CS → RS → US → S.
В этих вариантах последние этапы первой, второй и третьей схем моделирования могут быть реализованы после определения специфического состояния вещества в соответствии с пунктами В-1, В-2 и В-3. Они представляют собой расчет характеристик диагностического свойства вещества из данных о структурных параметрах и характеристик состояния.
Процедура реализации последней схемы моделирования описана ранее в пункте В-4.
Представление свойства S(ES) содержит информацию обо всех главных стратегиях прогнозирования неорганических веществ с необходимыми диагностическими свойствами и соответствующих проблемах прогнозирования.
1. Стратегия прогнозирования веществ с необходимыми композиционно-чувствительными свойствами:
((EC ⇒ C) ⇒ RC) ⇒UC ⇒ SC.
2. Стратегия прогнозирования веществ с необходимыми структурно-чувствительными свойствами:
((ER ⇒ R) ⇒ CR) ⇒ UR ⇒ SR.
3. Стратегия прогнозирования веществ с необходимыми кондиционно-чувствительными свойствами:
(((EU ⇒ U) ⇒ RU) ⇒CU) ⇒ SU.
Остальные возможные стратегии прогнозирования веществ с необходимыми специфическими состояниями, кристаллической структурой или химическим составом могут быть получены по аналогии из соответствующих представлений U(EU), R(ER) и C(EC).
Таким образом, на основе анализа структур математических теорий получены соответствующие концептуальные конструкты, в том числе эволюционно-фуркационный одноуровневый конструкт (EE4C4R4U4S4)(1), предназначенный для прогнозирования неорганических веществ с заданными свойствами. Соответствующая ему концептуальная система является модифицированным вариантом известной концептуальной системы структурных теорий химии. Сформулированы стратегии прогнозирования неорганических веществ с заданными свойствами, содержащие информацию о цели прогнозирования и о маршруте достижения этой цели. Дополненные конкретной информацией о классе неорганических веществ, стратегии позволяют сформулировать обобщенные задачи прогнозирования. Для каждой стратегии могут быть разработаны методы прогнозирования, сформулированы конкретные прогнозные задачи, решение которых позволит получить необходимые прогнозные данные.
Стратегия прогнозирования веществ с необходимыми структурно-чувствительными свойствами
При прогнозировании веществ с заданными свойствами и последующим целенаправленным поиском материалов с требуемыми для практического использования характеристиками необходимо решить ряд проблем. Одной из них является проблема достижения максимального соответствия прогнозной модели прогнозируемому объекту, т.е. проблема адекватности представления объекта моделью. Только теория прогнозирования веществ с заданными свойствами, если бы она была разработана, позволила бы осуществить максимально точный расчет свойства и обеспечить максимальную эффективность прогнозирования в целом [3]. В отсутствии такой теории максимальная адекватность представления и, следовательно, максимальная эффективность прогноза, по-видимому, не могут быть достигнуты в принципе, поскольку в процессе прогнозирования используются следующие приближения.
1. Свойства вещества определяются его химическим составом и строением. В общем случае любое свойство вещества (S) может быть представлено как линейная комбинация своих компонентов, которые определяются только составом (SC), структурой (SR) или состоянием (SU), с учетом соответствующих весовых коэффициентов: S = αSC +βSR + γSU (где α + β + γ = 1). В данном случае под состоянием U можно понимать дополнительный фактор, который определяется химическим составом и структурой вещества, а сам непосредственно определяет характеристики его диагностического свойства. Достаточно простая и относительно адекватная модель может быть построена только для веществ с одним, доминирующим компонентом свойства, т.е. для веществ с заданными структурно-чувствительными свойствами (S ≈ SR) или для веществ с заданными композиционно-чувствительными свойствами (S ≈ SC). Абстрагирование в каждом случае от остальных возможных компонентов свойства – суть первого приближения (приближение доминантного влияния одного из компонентов свойства) [3–5].
Процедура реализации процесса прогнозирования веществ с заданными свойствами включает три стадии: Моделирование → Прогнозирование → Расчет. С этими тремя стадиями прогнозирования связаны еще три приближения.
2. При моделировании вероятных структур веществ привлекаются идеализированные представления о взаимном расположении структурных элементов в объеме структурного фрагмента – носителя особого состояния, определяющего необходимое свойство [3]. Вероятные сокоординации структурных фрагментов в объеме элементарной ячейки кристаллической решетки вещества, допускаемые при моделировании, являются результатом комбинаторного перебора возможных наиболее симметричных структур (приближение идеализации вероятных структур).
3. Прогнозирование состава веществ с заданной кристаллической структурой наиболее эффективно, если оно осуществляется методом прогноза по функциональным критериям, которые учитывают наиболее вероятное проявление необходимых структурных особенностей, определяющих свойство, при условии сохранения структуры вещества [3, 4]. Стремление к минимизации количества функциональных критериев с целью упрощения процедуры прогнозирования может привести к снижению его эффективности (приближение минимизации критериев прогнозирования состава).
4. Расчет величины заданного свойства вещества по характеристикам его особого состояния, определяемым особенностями химического состава и кристаллической структуры вещества, может быть основан на использовании наблюдаемой корреляционной связи свойство – состояние с коэффициентом корреляции меньше единицы. В этом случае даже наличие сильной корреляционной связи может привести к снижению эффективности прогнозирования в целом [3–5] (приближение корреляционной связи свойство – состояние).
При прогнозировании многофазных материалов с заданными свойствами кроме описанных выше причин снижения эффективности предсказания возникают проблемы учета вклада свойств для каждой из фаз в свойство композиции и учета синергетического эффекта изменения этого свойства. В общем случае свойство композиции из i фаз можно представить следующим образом:
S = ∑aiSi + ΔS,
где Si и ai – свойство i-ой фазы и соответствующий весовой коэффициент, а ΔS – эффект синергизма фаз данной композиции. Отсюда следуют еще два приближения.
5. В простейшем случае синергетическим эффектом можно пренебречь (т.е. принять ΔS = 0), а величины коэффициентов ai принять пропорциональными соответствующим концентрациям или другим удельным (объемным и поверхностным) характеристикам фаз в материале (приближение аддитивности вклада свойств фаз в свойство композиции).
6. Учет влияния синергетического эффекта ΔS для неоднофазного материала хотя бы на качественном уровне связан с анализом комплексного состояния объекта прогнозирования, которое определяется химическим составом и структурой каждой из фаз, а также фазовым составом и микроструктурными характеристиками композиции в целом. Но даже в этом случае возможно определение тенденции изменения свойства (т.е. знака влияния синергизма) для композиции с учетом эффекта по сравнению с рассчитанным для нее свойством по аддитивной схеме (приближение аддитивности вклада свойств фаз с учетом возможного влияния синергетического эффекта).
Таким образом, в отсутствии строгой теории прогнозирования веществ с заданными свойствами прогноз их может быть только вероятностным, что существенно снижает его эффективность. Однако для определенных классов веществ возможно получение прогнозных данных на достаточно удовлетворительном уровне предсказания их составов, структур и величины свойств. Это, в частности, реализовано для катионных проводников и некоторых электродных материалов [3, 4, 8–10, 22–32, 42, 53, 54], для химически активных материалов и анодных покрытий [2, 11–21], для износостойких композиционных никель содержащих покрытий с антифрикционными свойствами [1, 6, 7, 33–41, 44–52, 55–59].
Выводы
Таким образом, представлен краткий обзор работ по методологическим основам прогнозирования неорганических материалов с необходимыми для применения свойствами.
На основе анализа структур математических теорий получены соответствующие концептуальные конструкты, в том числе эволюционно-фуркационный одноуровневый конструкт (EE4C4R4U4S4)(1), предназначенный для прогнозирования неорганических веществ с заданными свойствами. Соответствующая ему концептуальная система является модифицированным вариантом известной концептуальной системы структурных теорий химии.
Сформулированы стратегии прогнозирования неорганических веществ с заданными свойствами, содержащие информацию о цели прогнозирования и о маршруте достижения этой цели. Дополненные конкретной информацией о классе неорганических веществ, стратегии позволяют сформулировать обобщенные задачи прогнозирования.
Для каждой стратегии могут быть разработаны методы прогнозирования, сформулированы конкретные прогнозные задачи, решение которых позволит получить необходимые прогнозные данные.
Показана возможность реализации стратегии прогнозирования веществ с необходимыми структурно-чувствительными свойствами ((ER ⇒ R) ⇒ CR) ⇒ UR ⇒ SR на примерах ионных и суперионных проводников, электродных материалов, антифрикционных и износостойких композиционных материалов и покрытий.



