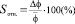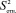Валидация аналитической методики – это экспериментальное доказательство того, что методика пригодна для решения предполагаемых задач. Валидации подлежат методики количественного определения, в том числе методики определения примесей и методики определения предела содержания действующих веществ. Каждую полученную по исследуемой методике аналитическую характеристику необходимо подкрепить экспериментальными данными. Заключительным документом при валидации аналитических методик являются Стандартные операционные процедуры (СОП), представляющие собой «документированные процедуры, содержащие описание процессов проведения испытаний» [5], подробно описывающие пошаговое выполнение определенной методики.
В продолжение темы валидации методик контроля качества и разработки СОП на примере анализа спирта этилового на содержание в нем спирта метилового и других токсических примесей в условиях Испытательной контрольно-аналитической лаборатории ГБУ РО «Центр по сертификации и контролю качества лекарственных средств» [9], в данной работе акцентируется внимание на контроле стабильности результатов анализа.
ГОСТ 30536-2013 [3] и ГОСТ 5962-2013 [4] регламентируют содержание токсичных микропримесей в спирте этиловом, наиболее опасными из которых являются: метанол – вызывает слепоту, в больших дозах летальный исход, и сивушные масла (смесь амилового, изоамилового, изобутилового, пропилового, изопропилового и др. спиртов) – вызывают кардио-, нефро- и гепатотоксический эффект, раздражающее действие, нервные расстройства, в ряде случаев кому. Этим примесям уделяется особое внимание при анализе спирта этилового.
Контроль стабильности результатов определения объемной доли метилового спирта в образце спирта этилового 95 % в лаборатории при реализации методики осуществляют по ГОСТ Р ИСО 5725-6-2002 [2]. При этом используется метод контроля стабильности стандартного отклонения промежуточной прецизионности и контроля стабильности показателей правильности с применением контрольных карт Шухарта (R-диаграмм, карт пределов). Периодичность контроля и процедуры контроля стабильности результатов измерений должны быть предусмотрены в Руководстве по качеству лаборатории.
На практике принято устанавливать один контролируемый период в квартал с продолжительностью 20–30 дней с ежедневными измерениями. Получают не менее 20 результатов контрольных измерений для построения карт Шухарта. При неудовлетворительных результатах контроля, например при превышении предела действия или регулярном превышении предела предупреждения, выясняют и устраняют причины этих отклонений.
Рекомендуется проводить проверку стабильности по результатам анализа образцов на содержание метилового спирта и пропанола-2. При одновременном контроле в лаборатории спирта и водки построение карт Шухарта проводят только для одного из этих продуктов [3].
Контрольные карты применяются [6] для контроля стабильности процесса измерений и выявления ситуаций выхода этого процесса из статистически контролируемого состояния. Они представляют собой графики, на которых по горизонтальной оси откладывают порядковый номер подгруппы, а по вертикальной – результаты измерения какого-либо показателя качества исследований. На эти карты наносятся в виде горизонтальных прямых «пределы», и выход результата за эти пределы свидетельствует о нестабильности процесса измерений. Результаты измерений не считаются стабильными, если имеется одна точка выше «предела действия» и пара последовательных точек выше «предела предупреждения».
Важным условием использования контрольных карт является то, что при переходе от одной подгруппы к другой должны меняться одни и те же условия. В химическом анализе могут изменяться факторы «время», «калибровка», «оператор» и «оборудование». В нашем случае от подгруппы к подгруппе изменяются факторы «время» и «оператор».
Прежде чем приступить к планированию эксперимента, необходимо убедиться в том, что опыты воспроизводимы. Надо отметить, что математические методы все больше используются в фармации [7]. Предварительно проверяют однородность дисперсии результатов анализа по критерию Кохрена [8,10], который используется для оценки однородности дисперсий результатов анализа. Однородность дисперсий означает, что среди всех дисперсий нет таких, которые бы значительно превышали остальные. Проводят несколько серий параллельных опытов в рассматриваемой области изменения влияющих факторов. Находят средние значения для каждой подгруппы:
, 
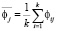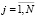, (1)
где φij – результат i-ого анализа в j-ой подгруппе,
j – номер подгруппы,
i – номер опыта в каждой подгруппе,
k – количество опытов в каждой подгруппе, проведенных при одинаковых условиях.
Далее вычисляют расхождение (оценку дисперсии) для каждой подгруппы:
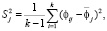
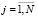. (2)
Для проверки воспроизводимости опытов, т.е. степени близости независимых результатов друг к другу, находят отношение наибольшей из оценок дисперсий к сумме всех оценок дисперсий:
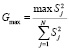, (3)
где Gmax – расчетное значение критерия Кохрена, которое сравнивается с критическим значением Gкр. этого критерия, как правило, при доверительной вероятности p = 0,95.
Результаты анализа образца этилового спирта 95 % на содержание метилового спирта для оценки стабильности стандартного отклонения промежуточной прецизионности σI (ТО)
|
Номер подгруппы (j = 1,2,…,N) |
Результат определения объемной доли метанола, % |
Δφ = │φ1-φ2│ |
|
|
|
|
|
φ1 |
φ2 |
|||||
|
1 |
0,00172 |
0,00172 |
0 |
0,00172 |
0 |
0 |
|
2 |
0,00171 |
0,00170 |
0,00001 |
0,00171 |
0,59 |
0,36 |
|
3 |
0,00167 |
0,00172 |
0,00005 |
0,00170 |
2,94 |
8,65 |
|
4 |
0,00165 |
0,00170 |
0,00005 |
0,00167 |
2,99 |
8,95 |
|
5 |
0,00167 |
0,00166 |
0,00001 |
0,00167 |
0,6 |
0,36 |
|
6 |
0,00165 |
0,00170 |
0,00005 |
0,00168 |
2,98 |
8,87 |
|
7 |
0,00177 |
0,00165 |
0,00012 |
0,00171 |
7,02 |
49,26 |
|
8 |
0,00178 |
0,00173 |
0,00005 |
0,00176 |
2,84 |
8,07 |
|
9 |
0,00170 |
0,00176 |
0,00006 |
0,00173 |
3,47 |
12,03 |
|
10 |
0,00163 |
0,00172 |
0,00009 |
0,00168 |
5,36 |
28,71 |
|
11 |
0,00162 |
0,00177 |
0,00015 |
0,00170 |
8,82 |
77,82 |
|
12 |
0,00174 |
0,00180 |
0,00006 |
0,00177 |
3,39 |
11,49 |
|
13 |
0,00175 |
0,00174 |
0,00001 |
0,00175 |
0,57 |
0,33 |
|
14 |
0,00174 |
0,00181 |
0,00007 |
0,00178 |
3,93 |
15,46 |
|
15 |
0,00180 |
0,00178 |
0,00002 |
0,00179 |
1,12 |
1,25 |
|
16 |
0,00176 |
0,00167 |
0,00009 |
0,00172 |
5,23 |
27,35 |
|
17 |
0,00164 |
0,00164 |
0 |
0,00164 |
0 |
0 |
|
18 |
0,00169 |
0,00176 |
0,00007 |
0,00173 |
4,05 |
16,4 |
|
19 |
0,00176 |
0,00172 |
0,00004 |
0,00174 |
2,3 |
5,3 |
|
20 |
0,00173 |
0,00174 |
0,00001 |
0,00174 |
0,57 |
0,33 |
= (φ1 + φ2)/2
Если Gmax ≤ Gкр, то проверяемую величину не считают выбросом и оставляют для дальнейшей статистической обработки. В противном случае проверяемое значение считают выбросом и исключают из дальнейших расчетов.
Рассмотрим методику проверки воспроизводимости опытов на примере анализа спирта этилового. Анализ спирта этилового осуществляется в соответствии с ГОСТ [3].
Испытания одного и того же образца проводились двумя провизорами-аналитиками в одной и той же лаборатории на одном и том же приборе. Образец спирта этилового 95 % подвергался анализу сначала одним провизором-аналитиком (φ1), затем анализировался повторно другим провизором-аналитиком на следующий день (φ2), и результаты испытаний ежедневно сравнивались. Для следующей подгруппы аналитиками аналогичным образом проверялся другой образец спирта. Таким образом, было проверено 20 подгрупп. Расхождения рассчитывались для N = 20 подгрупп, каждая из которых содержит две пробы.
Для рассматриваемого случая двух измерений (k = 2) в подгруппе соотношения (1)–(2) принимают следующий вид:
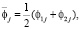
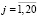, (4)
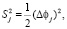
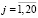, (5)
где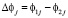 
.
Здесь переменные величины несут следующую смысловую нагрузку:
φ1j, φ2j – значения объемной доли метилового спирта в каждой подгруппе,
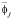– среднее значение объемной доли метилового спирта в каждой подгруппе,
∆φj – абсолютное значение расхождения результатов анализа по каждой подгруппе.
Согласно ГОСТ [2] для сопоставления результатов определения объемной доли спирта метилового в спирте этиловом рассчитывают относительное расхождение в процентах Sj, отн = (∆φj/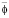
)∙100( %) по каждой подгруппе, квадрат относительного расхождения и сумму квадратов относительного расхождения по всем подгруппам 
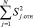. При этом формула расчета критерия Кохрена приобретает следующий вид:
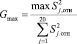. (6)
Подставляя значения из таблицы в формулу (6), получаем значение критерия Кохрена:
,
где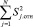 
– сумма среднеквадратичных отклонений для заданного N.
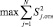– максимальное значение их среднеквадратичных отклонений для заданного N.
Для рассматриваемых условий эксперимента при доверительной вероятности p = 0,95 критическое значение критерия Gкр. = 0,389 [2]. Как видим, в этом случае Gmax < Gкр.. Следовательно, признается однородность дисперсий, а значит, и воспроизводимость опытов.
Применяя метод контрольных карт Шухарта к результатам измерений, представленным в таблице, после подтверждения однородности дисперсии по расхождениям Sjотн проверяют стабильность этих результатов измерений и оценивают стандартное отклонение промежуточной прецизионности с изменяющимися факторами «время» и «оператор».
Мерой «промежуточной прецизионности» является дисперсия σI2(ТО) промежуточной прецизионности или стандартное отклонение σI(ТО) промежуточной прецизионности, рассчитываемое по формуле
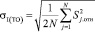, (7)
где N – количество подгрупп.
Для расчета параметров контрольной карты Шухарта используют стандартное отклонение промежуточной прецизионности с изменяющимися факторами «время» и «оператор», которое устанавливают до начала первого контрольного периода (контрольный период – период проведения внутрилабораторного контроля качества измерений). На основании значения σI (ТО) рассчитывают параметры контрольной карты Шухарта с использованием соответствующих коэффициентов. При расчете средней линии и верхних контрольных пределов UCL (Upper Confidence Limit) используют коэффициенты, приведенные в ГОСТ Р 50779.42 [1] (1,128; 3,686; 2,834 при числе наблюдений в подгруппе, равном 2) по формулам:
а) средняя линия
L = 1,128∙σI (ТО) = 1,128∙2,65 = 2,99,
где 1,128 – коэффициент для средней линии;
б) пределы действия
UCLд = 3,686∙σI (ТО) = 3,686∙2,65 ≈ 9,77,
где 3,686 – коэффициент для предела действия;
в) пределы предупреждения
UCLпр = 2,834∙σI (ТО), ≈ 2,834∙2,65 ≈ 7,51,
где 2,834 – коэффициент для числа предупреждения.
Полученные значения используют для построения карты пределов (рисунок).
В данном случае превышение предела действия отсутствует, а превышение предела предупреждения носит нерегулярный, однократный, случайный характер. Карта пределов для содержания метанола (объемные %), полученных в условиях повторяемости, приведенная на рисунке, свидетельствует, что результаты являются стабильными и методика может использоваться. В рассматриваемом случае стандартное отклонение σI (ТО) промежуточной прецизионности равно
.
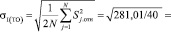
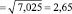При нестабильных результатах измерений вычисляют значение стандартного отклонения промежуточной прецизионности после исключения подгруппы с расхождением, превышающим предел действия. Допускается исключать не более двух подгрупп, при большем их количестве анализируют и устраняют причины нестабильности, проводят новый набор (больше 20 пар φ1 и φ2) и рассчитывают новые значения стандартного отклонения σI (ТО). Доказав, что результаты получаются стабильными, оценку стандартного отклонения промежуточной прецизионности можно в дальнейшем использовать для расчета параметров контрольных карт переделов для следующего контрольного периода.
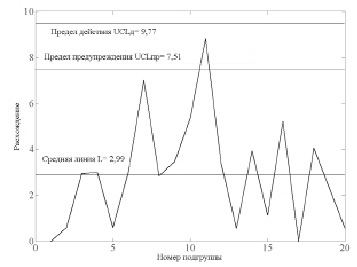
Контрольная карта Шухарта при контроле стабильности результатов определения объемной доли метилового спирта в образце спирта этилового 95 % с изменяющимися факторами «время» и «оператор»
Таким образом, доказана стабильность результатов при использовании методики оценки качества спирта этилового 95 % в соответствии с требованиями нормативных документов в условиях Испытательной контрольно-аналитической лаборатории ГУЗ «Центр сертификации и контроля качества лекарственных средств Рязанской области» с использованием контрольных карт Шухарта. Результаты проведенных анализов могут быть использованы при разработке Стандартной операционной процедуры «Валидация газохроматографического метода испытаний спирта этилового 95 %».