В поликристаллических металлах влияние среднего размера зерна d на величину предела текучести σт принято описывать с помощью соотношения Холла - Петча:
σТ = σ0 + Kd –1/2, (1)
где σ0 – напряжение, характеризующее сопротивление пластической деформации со стороны кристаллической решетки и дефектов решетки, препятствующих движению решеточных дислокаций; K – коэффициент, характеризующий вклад в упрочнение со стороны границ зерен.
В работе [1] показано, что существует около десятка различных моделей, которые не до конца могут объяснить нарушение закона Холла – Петча (ХП) при размерах зерен меньше критического. Считается, что традиционная деформация по дислокационному механизму в материалах с размером зерна меньше 30 нм невозможна ввиду малой вероятности появления подвижных дислокаций.
Некоторые модели соотношения Холла – Петча
В работах [2, 3] рассмотрено несколько моделей ХП:
– модель «скоплений», объясняющая влияние размера зерна на σт концентрацией напряжений в скоплениях дислокаций, моделирующих индивидуальные полосы скольжения;
– модель деформационного упрочнения, объясняющая соотношение (1) зависимостью плотности дислокаций или длины их пробега от размера зерна;
– модель, использующая представление об особенностях механизмов работы поверхностных или зернограничных дислокационных источников в процессе передачи скольжения от зерна к зерну;
– модель, базирующаяся на представлениях о двух типах дислокаций – статически запасенных и геометрически необходимых.
Указанные модели позволяют качественно объяснить степенной характер зависимости предела текучести от размера зерна в предположении о постоянстве параметра K. Вместе с тем к настоящему времени накоплен большой объем экспериментальных данных, которые не удается интерпретировать в рамках традиционных представлений о постоянстве параметра K. В частности, в ряде экспериментальных работ обнаружена существенная зависимость коэффициента K от степени и скорости предварительной деформации, температуры и времени предварительного дорекристаллизационного отжига и т.д.
В работах [4, 5] показано, что в нано-микрокристаллических металлах (НМК) металлах с размером зерна d ~ (0,1–0,2) мкм при напряжениях порядка предела текучести дислокационные скопления могут и не возникать, хотя работа дислокационных источников Франка – Рида возможна.
Вопрос о вкладе зернограничного проскальзывания в общую долю деформации НМК металлов (при комнатной температуре) также весьма неоднозначен и спорен и до настоящего времени остается открытым.
Нарушение закона Холла – Петча экспериментально исследовано в работе [6] и теоретически в работе [7], а также во многих других работах [1–3].
Примером компьютерного моделирования является работа [8], где в рамках инженерии границ зерен выявлены два типа ротационно-волновых потоков, которые определяются углом разориентации смежных зерен. Первый тип зернограничных потоков развивается в малоугловых границах и генерирует в объем зерен дислокации, определяющие прямой эффект Холла – Петча. Второй тип зернограничных потоков развивается в большеугловых границах и приводит к обратному эффекту Холла – Петча.
В работе [9] для предела текучести нами получено
σТ = σМ + Cσd –1/2. (2)
Уравнение (2) по форме совпадает с уравнением Холла – Петча (1). Однако коэффициенты пропорциональности в обеих формулах различаются. В рассматриваемом случае поведение предела текучести малых частиц определяется также величиной их поверхностного натяжения ?.
Для малых d А.И. Русанов получил асимптотическую линейную зависимость [10]:
σ = Kd. (3)
Здесь K – коэффициент пропорциональности. Формула (3) получена на основе термодинамического рассмотрения и должна быть применима к малым объектам различной природы.
В этом случае уравнение (2) принимает вид
σТ = σМ + CKd 1/2. (4)
Уравнение (4) представляет собой обратный эффект Холла – Петча. Таким образом, обратный эффект Холла – Петча обусловлен размерной зависимостью поверхностного натяжения наночастиц, начиная с некоторого критического радиуса, значения которого для 55 чистых металлов определены в [9].
На рисунке показаны зависимости ХП для меди и никеля.
Обработка кривых рисунка с помощью соотношения (2) дала значение постоянной С:
C ≈ 102 МПа•м1/2. (5)
Необходимо отметить следующее: постоянная С имеет одно и то же значение для большинства металлов периодической системы элементов. Это позволяет объяснить наблюдаемую зависимость коэффициента K в уравнении ХП от типа металла через различие в величине поверхностного натяжения для различных металлов.
Используя табличные данные по величине σМ [12] и определяя величину поверхностного натяжения по методике [13], мы можем рассчитать предел текучести для тех металлов, для которых известна величина σМ. Для ряда металлов результаты таких расчетов приведены в таблице.
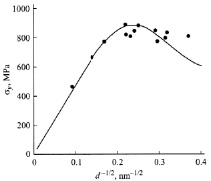
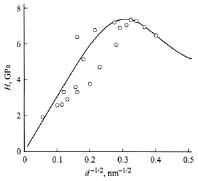
а б
Соотношение ХП для предела текучести нанокристаллической меди (а) и микротвердости никеля (б) [11]
Предельная текучесть микро- и наночастиц некоторых металлов
|
Металл |
σ0, МПа [290] |
σ, Дж/м2 |
σТ, МПа d = 16 нм |
σТ, МПа d = 64 нм |
σТ, МПа d = 100 нм |
σТ, МПа d = 225 нм |
|
Алюминий |
22 |
0,653 |
38 |
30 |
28 |
26 |
|
Бериллий |
230 |
1,091 |
257 |
244 |
241 |
237 |
|
Ванадий |
106 |
1,512 |
144 |
125 |
121 |
112 |
|
Вольфрам |
760 |
2,587 |
825 |
792 |
786 |
777 |
|
Гафний |
500 |
1,754 |
544 |
529 |
518 |
507 |
|
Железо |
170 |
1,268 |
202 |
186 |
189 |
178 |
|
Золото |
40 |
0,936 |
64 |
56 |
49 |
44 |
|
Иридий |
90–100 |
1,917 |
138–148 |
122–132 |
109–119 |
98–108 |
|
Ниобий |
210 |
1,919 |
258 |
242 |
229 |
218 |
|
Палладий |
60 |
1,279 |
92 |
81 |
73 |
65 |
|
Платина |
70 |
1,429 |
106 |
94 |
84 |
76 |
|
Родий |
70–100 |
1,567 |
109–139 |
96–126 |
86–116 |
76–106 |
|
Рутений |
300–400 |
1,825 |
346–446 |
331–431 |
318–418 |
307–407 |
|
Серебро |
20–30 |
0,865 |
42–52 |
35–45 |
29-39 |
23-33 |
Из таблицы следует, что предел текучести для частиц размером 0,3–0,5 микрон практически совпадает с соответствующей величиной для массивного образца.
Заключение
Изложенный в настоящей работе подход не касается микромеханизмов процессов упрочнения и разупрочнения наноструктур. Однако он может быть полезен для инженерии наноматериалов, поскольку определена явно связь механических свойств наноструктур с их поверхностным натяжением (поверхностной энергией).



