Многолетний опыт эксплуатации магистральных нефте- и продуктопроводов показывает, что несмотря на самые высокие требования, предъявляемые к надежности и большие финансовые затраты на своевременное и качественное техническое обслуживание, безотказная их работа невозможна [1–10]. Особую опасность представляют подводные переходы, на долю которых приходится до 2 % общей протяженности магистралей. Несмотря на плановые диагностические обследования, замену труб и т.п. на подводные переходы происходят большое количество отказов, которые нередко сопровождаются также серьезными последствиями для окружающей среды.
Анализ некоторых аварийных ситуаций показывает, что величины нанесенного ущерба определяются, когда авария и ее последствия уже произошли. Не случайно по проблеме принят ряд нормативных документов, согласно которым время локализации разлива и сбора нефти не должно превышать 4 ч.
Для сбора плавающей нефти используются различная техника и технологии: механические, химические, биологические способы, сорбенты-нефтепоглотители.
Однако многолетний опыт борьбы с нефтяными загрязнениями на водных объектах показывает, что существующие технологии и технические средства неэффективны при наличии течения, на мелководных водоемах, а также при доочистке любых водных объектов от следов нефти. Они предназначены в основном для использования в области положительных температур. Неразрешенность проблемы сбора нефти с поверхности воды в зимних условиях была подтверждена в ходе ликвидации последствий аварии на ПП МН ТОН-II.
Физическое моделирование сложных стохастических систем, как известно, процесс дорогостоящий и весьма трудоемкий. В этой связи математическое описание и моделирование многопараметрического процесса с целью выявления наилучших показателей удаления жидких и полутвердых углеводородов с водной поверхности может дать ощутимые выгоды.
Одним из наиболее широко применяемых способов является сбор нефти с поверхности водоемов при помощи медленно вращающегося барабана (скиммера). Ввиду сложности процессов до настоящего времени не разработано математическое описание гидродинамических и теплофизических процессов в скиммере. Скиммер предназначен для ликвидации нефтяных загрязнений с водной поверхности.
Постановка задачи
На рисунке приведена схема барабанного сборщика. Барабан скиммера частично погружен в воду на глубину R + H, где R – радиус барабана. Также глубину погружения можно определять через угол ψ. Обозначим толщину нефтяного слоя на поверхности воды h, а скорость поступательного движения оси барабана  относительно нефтяного пятна, которое учитывает и собственную скорость движения скиммера и течения нефтяного слоя. Поверхность нефтебитума на поверхности ротора обозначим S, динамическая вязкость нефтяного слоя выражается соотношением η = νρ, где ν – кинематическая вязкость, а ρ – плотность вязкой жидкости. Барабан скиммера вращается с угловой скоростью
относительно нефтяного пятна, которое учитывает и собственную скорость движения скиммера и течения нефтяного слоя. Поверхность нефтебитума на поверхности ротора обозначим S, динамическая вязкость нефтяного слоя выражается соотношением η = νρ, где ν – кинематическая вязкость, а ρ – плотность вязкой жидкости. Барабан скиммера вращается с угловой скоростью  .
.
Решение задачи о сборе нефтепродуктов с поверхности водоемов, естественно, ищем в цилиндрических координатах. Выберем цилиндрические координаты с осью z вдоль оси цилиндра, линия r направлена вдоль радиуса барабана (рис. 1).
Для описания поля скорости при захвате нефтебитума вращающимся барабаном использовано уравнение Навье – Стокса с учетом силы гравитации
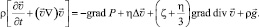
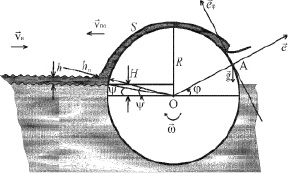
Схематическое представление барабанного скиммера
Из рис. 1 видно, что радиальная и угловая составляющие силы тяжести определяются выражением
gr = –g sin φ; gφ = –g cos φ.
Уравнение неразрывности, если мы будем считать, что вязкая жидкость практически несжимаема, будет иметь вид
 (1)
(1)
Уравнение Навье – Стокса для несжимаемой жидкости упрощается и приобретает следующий вид:
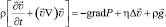 (2)
(2)
На достаточном удалении от торцевых концов ротора нефтесборщика движение собираемой жидкости определяется только двумя полярными координатами r и φ и не зависит от осевой координаты z. В предложении бесконечного цилиндра уравнения для координат 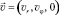 имеют вид
имеют вид
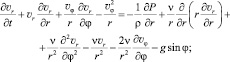
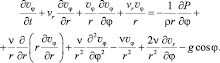
Уравнение неразрывности несжимаемой жидкости в полярных координатах представляется как
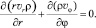 (3)
(3)
Полная постановка задачи включает также граничные условия на поверхности нефтесборщика, которые определяются из условия прилипания жидкости к поверхности. В пограничной области r = R тангенциальная скорости жидкости vφ и поверхности цилиндра ωR совпадают:
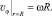 (4)
(4)
Поверхность ротора скиммера непроницаема, поэтому нормальная компонента скорости vr обращается в нуль при r = R
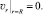 (5)
(5)
Условие на границе соприкосновения S собираемого битума и воздуха определяются атмосферным давлением. Будем полагать, что тангенциальная составляющая тензора вязких напряжений обращается в нуль
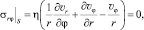 (6)
(6)
нормальная – равна атмосферному давлению P0
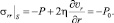 (7)
(7)
В начальный момент времени будем считать, что жидкость и барабан скиммера находятся в состоянии покоя
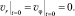 (8)
(8)
Для расчета производительности установки рассмотрим стационарное течение жидкости, т.к. в случае длительной работы скиммера движение жидкости устанавливается. В этом случае поле скорости можно считать стационарным:
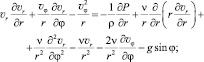 (9)
(9)
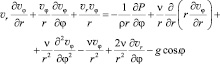 (10)
(10)
Предположим, что толщина слоя захватываемого битума h много меньше радиуса скиммера R (h/R << 1). В этом случае линии тока с большой точностью будут параллельны поверхности скиммера, тогда радиальной составляющей скорости можно пренебречь vr = 0. Тангенциальная составляющая скорости не зависит от φ, а определяется только координатой r. В предположении тонких слоев можно считать, что значения координаты r велики, поскольку r > R, тогда всеми слагаемыми, содержащими r в знаменателе, можно пренебречь:
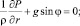 (11)
(11)
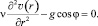 (12)
(12)
Граничные условия на поверхности скиммера запишутся следующим образом:
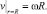 (13)
(13)
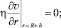 (14)
(14)
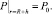 (15)
(15)
Окончательное выражение для распределения скоростей имеет вид
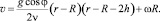 (16)
(16)
Анализ выражения (16) показывает, что при малых угловых скоростях вращения барабана значения скорости становятся отрицательными, что не может реализоваться на практике. Поэтому полученное решение позволяет определять минимальную угловую скорость вращения барабана, при превышении которой установка начинает функционировать.
Масса жидкости, увлекаемая в единицу времени через поперечное сечение, соответствующее φ = ψ, определяется путем интегрирования (16) в пределах от R до R + hн.
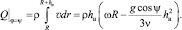 (17)
(17)
Из условий Q = 0 получим min частоту вращения барабана
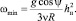 (18)
(18)
Таким образом, решение (16) справедливо только для ω > ωmin.
На самом деле толщина пленки hп является функцией от угловой координаты φ hп = hп(φ). Для того, что бы определить эту зависимость, найдем Q согласно (17) для произвольного угла φ
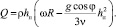 (19)
(19)
Ввиду того, что Q не должно зависеть от угла φ, получим уравнение для определения hп(φ), уравнение для определения профиля поверхности hп нефтебитума относительно поверхности барабана скиммера
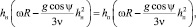
где hн – толщина слоя при некотором фиксированном угле φ = ψ′.
Это уравнение сводится к кубическому уравнению вида x3 + px + q = 0, которое в свою очередь решается по формуле Кардано, где
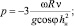
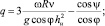
и 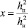 . Решение этого уравнения будет иметь вид
. Решение этого уравнения будет иметь вид
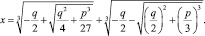 (20)
(20)
Из (17) мы можем определить толщину нефтяной пленки на всей поверхности барабана
 (21)
(21)
где q зависит от hн.
Итак, разработанная математическая модель позволяет успешно рассчитывать производительность скиммера от различных параметров.
Таким образом, в работе осуществлена постановка гидродинамической задачи сбора жидких углеводородов с поверхности воды барабанным скиммером. Анализ полученных выражений показывает, что при малых угловых скоростях вращения барабана значения скорости становятся отрицательными, что не может реализоваться на практике, а при больших угловых скоростях вращения барабана значение производительности резко падает в виду отрыва пленки от барабана. Поэтому полученное решение позволяет определять минимальную и максимальную угловые скорости вращения барабана, в пределах которых установка начинает функционировать.
Преимуществом развитой здесь математической модели является то обстоятельство, что она базируется на точном решении задачи, в то время как использовавшиеся ранее строились на приближенных решениях.



