В настоящее время широкое применение находят эмульсионные взрывчатые вещества (ЭВВ), имеющие ряд существенных преимуществ перед другими типами промышленных ВВ. В составе ЭВВ отсутствуют взрывчатые компоненты, они водоустойчивы, дешевы, отличаются низкой чувствительностью к механическим воздействиям и позволяют осуществлять их механизированное изготовление и заряжание. Один из способов сенсибилизации смеси состоит во введении в нее раствора газогенерирующей добавки, содержание и концентрация которой регулируют конечную плотность ЭВВ. Однако газовые пузырьки, распределенные в эмульсии и выполняющие функцию «горячих точек», сжимаются под действием гидростатического давления колонки заряда, приводя к увеличению плотности ЭВВ по мере возрастания глубины скважины.
Вследствие ухудшения условий открытой разработки полезных ископаемых – увеличение крепости и обводненности пород с глубиной в карьерах, обеспечение необходимого качества дробления горных пород без существенного увеличения затрат возможно только за счет интенсификации буровзрывных работ (БВР), одним из основных направлений которой является оптимизация параметров скважинной отбойки. Имеющиеся на сегодняшний день расчетные методики для их определения обладают рядом недостатков и требуют усовершенствования в части более полного учета особенностей взрывного процесса в среде. Следовательно, совершенствование методов определения параметров БВР является актуальной научной задачей и имеет большое практическое значение [7].
Рассмотрим пузырек газа в нитроните Э-70. Давление в пузырьке (рис. 1):
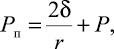 (1)
(1)
где δ – коэффициент поверхностного натяжения; r – радиус пузырька; Р – давление в окружающем пузырьке нитронита Э-70.
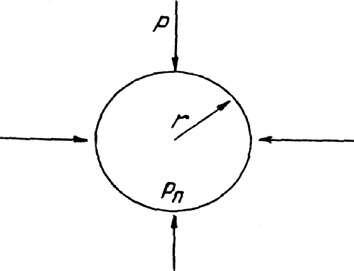
Рис. 1. Давление в пузырьке
Рассмотрим скважинный заряд нитронита Э-70 (рис. 2). Введем обозначения: Lз – длина заряда нитронита Э-70; Ро – давление на верхний торец заряда; ρс – плотность эмульсии (не аэрированной); ρо – плотность ВВ при заряжании; Р(х) – давление в заряде в сечении (на глубине х относительно верхнего торца заряда); ρ(х) – плотность в заряде в сечении х.
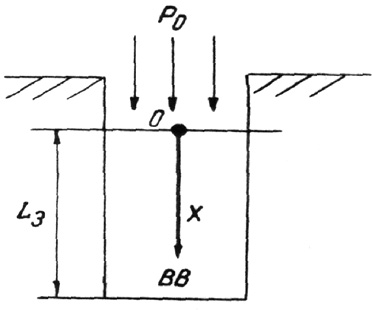
Рис. 2. Скважинный заряд нитронита Э-70
Эмульсия состоит из двух несмешивающихся жидкостей. Поэтому максимальную плотность можно рассчитать через удельные объемы, занимаемые каждой жидкостью в эмульсии [1, 2, 5].
Пусть Vc = 1/ρс – удельный объем эмульсии; Vг(х) – удельный объем газа в сечении х. Тогда
ρ(х) = (Vc + Vг(х))–1, (2)
где Vc = const.
Количество пузырьков N в любом сечении х постоянно ввиду большой вязкости нитронита Э-70 (нет распределения по х вследствие диффузного движения пузырька). Тогда
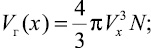 (3)
(3)
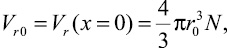 (4)
(4)
где Vr0 – удельный объем газовой фазы при заряжании; r0 – начальный радиус пузырька при заряжании. Тогда из (3) и (4)
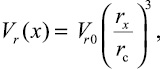 (5)
(5)
где rx – радиус пузырька в сечении х.
Подставляем (5) в (2):
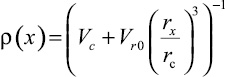
или
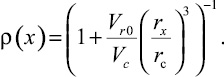 (6)
(6)
Здесь 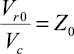 , Z0 – степень аэрации нитронита при заряжании. В других обозначениях
, Z0 – степень аэрации нитронита при заряжании. В других обозначениях 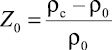 . Учитывая, что 1/Vc = ρc, выражение (6) можно представить:
. Учитывая, что 1/Vc = ρc, выражение (6) можно представить:
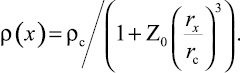 (7)
(7)
Рассмотрим теперь элемент объема заряда на глубине х толщины Δх (рис. 3).
Из условия равновесия данного элемента следует:
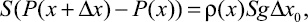 (8)
(8)
где S – площадь сечения заряда. Здесь учтено, что при достаточно малом Δх можно считать плотность в данном элементе постоянной и равной Δ(х). Тогда (8) имеет вид 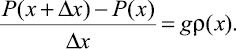 При ρх > 0 получаем
При ρх > 0 получаем 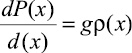 . Подставляя (7), имеем
. Подставляя (7), имеем
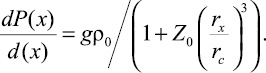 (9)
(9)
Пусть теперь сжатие пузырьков происходит адиабатически (распределение ρ(х) устанавливается в заряде до наступления существенного остывания нитронита). Тогда
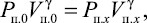 (10)
(10)
где Pп.0 – давление в пузырьке при заряжании; Pп.x – давление в пузырьке, расположенном в сечении х; Vп.0 – объем газа пузырька при заряжании; Vп.x – объем газа пузырька, находящегося в сечении x; γ = 1,25 – показатель адиабаты.
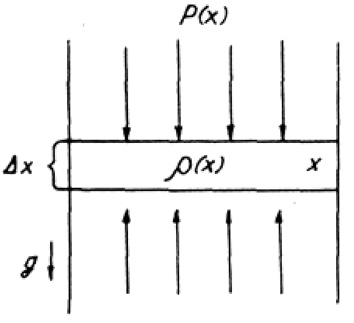
Рис. 3. Элемент объема заряда
С учетом (1) формулу (10) можно записать в виде
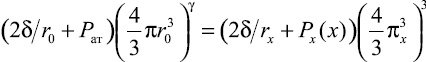
или
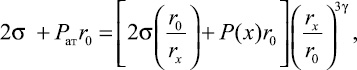 (11)
(11)
где Рат – атмосферное давление.
Уравнения (9) и (11) полностью описывают поставленную задачу, если их дополнить начальными условиями: при х = 0
Рх = Р0; rx = r0. (12)
Введем обозначение α = rx/r0. Тогда получается система уравнений (9), (11), (12)
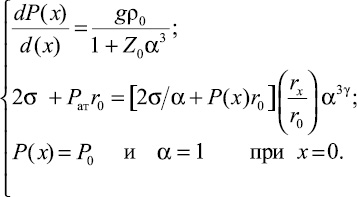 (13)
(13)
Из (13) при заданных g, ρc, ρ0, r0, Р0, Рат, δ можно получить Р(х), α(х) в любом сечении х, после чего по (7) определяется и ρ(х). Если пренебречь поверхностным натяжением (δ = 0), то (13) принимает вид
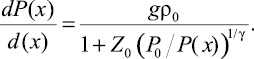
В этом случае α3(х) = P(x)1/γ.
Из общего вида системы (13) видно, что она не имеет аналитического решения, следовательно, требует численного решения. Опишем его алгоритм.
Дифференциальное уравнение (13) совместно с начальными условиями является задачей Коши, которую решаем наиболее простым методом – разностным методом Эйлера (рис. 4) по причине достаточной гладкости и монотонности функций P(x) и ρ(х).
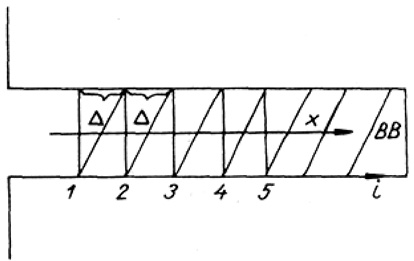
Рис. 4. Разностный метод Эйлера
Алгоритм решения:
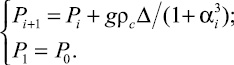 (14)
(14)
Второе уравнение системы (13) является трансцендентным. Его решаем итерационным методом – методом бисекции:
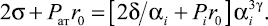 (15)
(15)
После этого на каждом шаге по х определяем плотность:
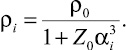 (16)
(16)
Уравнения (14)–(16) решаются совместно. Для этого данный алгоритм реализован в виде программы PUZ на ЭВМ.
Входными данными являются: ρc, ρ0, r0, Р0, Рат, δ. Выходными х, P(x), ρ(х), ρ(х), (х), δ, где δ(х) = (ρ(х) – ρ0/ρ0.
Здесь Р0 берется в общем виде и имеет вид
Р0 = Рат + ρзабgLзаб,
где ρзаб – плотность забойки (например, воды); Lзаб – длина забойки.
Если Lзаб = 0, то забойка отсутствует.
Оценочные результаты приведены в таблице.
Таким образом, можно сделать следующие выводы:
1. При r0 = 0,1 – 0,01 мм P(x) и ρ(х) практически не зависят от σ (при σ < σмаз).
2. При r0 = 0,01 мм P(x) и ρ(х) зависят от r0 и σ.
3. Наличие забойки существенно сказывается на P(x) и ρ(х).
4. На глубине больше 10 м ρ(х) > 1,3 г/см3.
Для расчета зависимости плотности нитронита Э-70 по глубине скважины использованы исходные следующие данные.
Высота водяной забойки равна 7 м. Это значение является максимальным для скважины глубиной до 35 м [2]. В случае, если высота забойки будет меньше, уменьшится гидростатическое давление на эмульсионное ВВ в нижней части скважины, что повысит его детонационную способность. Максимальная предельная плотность нитронита по ТУ 7276-003-58995878-2004 принята равной 1,25 г/см3 [3, 4, 6].
Плотность нитронита Э-70 на различной глубине скважины рассчитывается следующим образом. На слой эмульсионного ВВ, находящегося в скважине на глубине Н, действуют следующие силы: РА – атмосферное давление; РВ – гидростатическое давление столба воды высотой Δhв; Р1 – гидростатическое давление столба эмульсионного ВВ высотой Δh1) [3, 4, 8].
Атмосферное давление РА принимаем равным 980 Па. Гидростатическое давление столба воды высотой Δhв = 7 м; Рв ~ 686 Па.
Гидростатическое давление столба ЭВВ высотой Δh можно выразить как ΔР = ρЭВВ•Δh (кг/см2), т.е. значение ΔР будет зависеть от высоты слоя Δh и плотности эмульсионного ВВ, которая непрерывно изменяется по высоте этого слоя.
Оценочные результаты
|
σ, н/м |
ρ0, атм |
r, мм |
х, м |
P(x), атм |
ρ,г/см3 |
δ(х), % |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0,0355 (мазут) |
1 (без забойки) |
0,05 |
8 |
1,992 |
1,290 |
3,221 |
|
12 |
2,500 |
1,300 |
3,984 |
|||
|
18 |
3,267 |
1,309 |
4,729 |
|||
|
1 (без забойки) |
0,10 |
8 |
1,992 |
1,290 |
3,221 |
|
|
12 |
2,500 |
1,300 |
3,984 |
|||
|
18 |
3,267 |
1,309 |
4,729 |
|||
|
1,668 (6 м воды) |
0,05 |
8 |
2,696 |
1,303 |
4,207 |
|
|
12 |
3,208 |
1,309 |
4,682 |
|||
|
18 |
3,979 |
1,315 |
5,192 |
|||
|
1,668 (6 м воды) |
0,001 |
8 |
2,688 |
1,292 |
3,394 |
|
|
12 |
3,196 |
1,298 |
3,860 |
|||
|
18 |
3,961 |
1,305 |
4,402 |
|||
|
0 |
1 |
0,05 |
8 |
1,993 |
1,291 |
3,242 |
|
12 |
2,500 |
1,300 |
4,003 |
|||
|
18 |
3,268 |
1,309 |
4,750 |
|||
|
1,668 |
0,5 |
8 |
2,696 |
1,303 |
4,229 |
|
|
12 |
3,208 |
1,309 |
4,703 |
|||
|
18 |
3,979 |
1,315 |
5,212 |
Примечание. ρc = 1,35 г/см3, ρ0 = 1,25 г/см3.
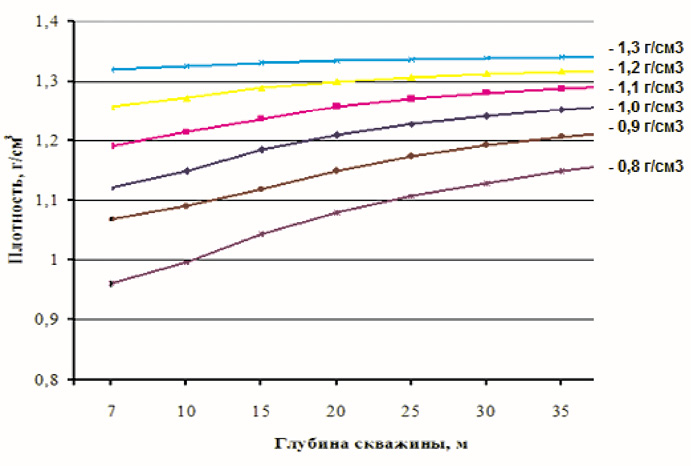
Рис. 5. Изменение плотности нитронита Э-70 в колонке заряда по глубине скважины при различной исходной плотности
Для того чтобы рассчитать плотность на определенной глубине скважины, зададимся каким-либо фиксированным значением Р1. Тогда давление, под которым будет находиться слой эмульсионного ВВ на глубине Н, РН1 = РА + РВ + Р1; РH1 ≈ 1666 Па.
Увеличивая последовательно высоту заряда на слой, равный 5 м, рассчитывая аналогичным образом плотность ЭВВ на нижней границе этого слоя, можно проследить изменение плотности эмульсионного ВВ, размещенного на различной глубине скважины. В качестве забойки принят столб воды высотой 7 м. Расчеты сделаны для нитронита Э-70 с различной исходной плотностью (0,8; 0,9; 1,0; 1,1; 1,2; 1,3) г/см3, а их результаты представлены на рис. 5.
Пользуясь этими данными, можно определить плотность нитронита Э-70 для конкретного случая заряжания скважин любой глубины.
Например, необходимо зарядить обводненные скважины глубиной 20 м. На рис. 5 на оси абсцисс находим глубину скважин, равную 20 м, и идем вверх по вертикали до пересечения с прямой, отвечающей критической плотности, которая для зарядов в прочной оболочке диаметром 250 мм равняется 1,26 г/см3. Таким образом, заряжать скважины глубиной 20 м следует с исходной плотностью, указанной цифрами у кривых, лежащих ниже горизонтальной прямой критической плотности и левее вертикальной прямой, соответствующей глубине скважины 20 м. Согласно рис. 5 для рассматриваемого примера начальная (исходная) плотность нитронитов Э-70 не должна превышать 1,1 г/см3 [4].
Массу заряда, которую надо зарядить в скважины различной глубины при различной исходной плотности, можно определить по рис. 6. Для рассматриваемого примера она составит 750 кг.
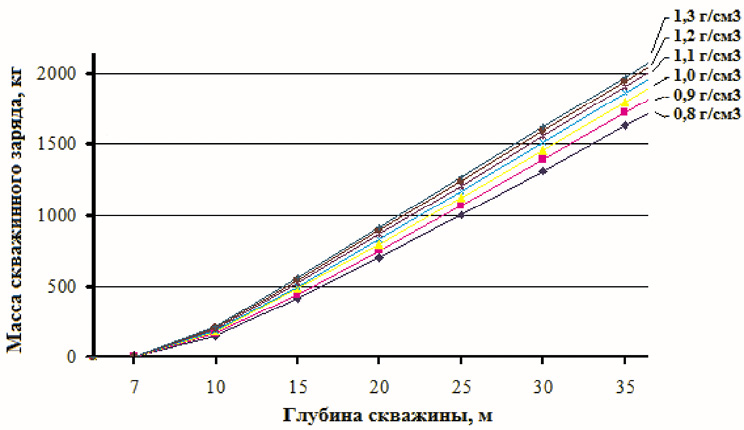
Рис. 6. Зависимость массы заряда нитронита Э-70 от глубины скважины: предельная плотность – 1,3 г/см3, dскв = 250 мм; забойка – буровая мелочь; РАВ = 1,7 кг/см2
Аналогично можно провести расчеты для эмульсионных ВВ любой другой плотности при забойке любой высоты с любым удельным весом. Массу заряда, которую нужно зарядить в скважины разной глубины при различной, исходной плотности нитронита Э-70, можно определить по номограмме (рис. 6). Пользуясь этими данными, можно определить исходную плотность нитронита Э-70 для конкретного случая заряжания скважин той или иной глубины.
При глубине скважины более 35 м и при плотности заряжания более 1,3 г/см3 могут произойти отказы в скважинах, что может привести к несчастным случаям при взрывных работах, а обеспечение надежной детонации скважинных зарядов ВВ является одним из важнейших направлений повышения безопасности взрывных работ.



