Твердотельные электрохимические источники ЭДС являются наиболее востребованными источниками энергии для микроэлектронной промышленности. В связи с этим интерес исследователей направлен на поиск новых более эффективных механизмов и способов генерации электрической энергии. В работе [8] описан термовольтаический эффект, заключающийся в возникновении электрического напряжения между противоположными гранями полупроводникового образца сульфида самария SmS при его нагреве до 400–500 K. Эффект проявлялся при наличии градиента концентрации донорной примеси, направленного в направлении расположения этих граней. Электрическое напряжение возникало при отсутствии градиента температуры вдоль направления расположения электродов на образце при нагреве, и поэтому не может быть объяснено классическим термоэлектрическим эффектом Зеебека. Известен целый ряд таких неравновесных явлений в сегнетоэлектриках, которые не имеют однозначного теоретического описания. В частности, авторы [7] привлекают микроскопические механизмы существования неравновесных токов в сегнетоэлектриках, которые могут существовать долговременно. В работах [1, 2, 6, 9] описана термостимулированная ЭДС, возникающая только в высоколегированном железом кристалле ниобата лития с напыленными электродами из пары различных металлов. Знак термоЭДС определяется положением электродов, нанесенных напылением в вакууме на противоположные грани кристалла, и не зависит от ориентации кристаллографических осей образца относительно электродов.
В данной работе приведены результаты экспериментального исследования термостимулированных токов в тонкослойной структуре металл – ниобат лития – металл.
В отличие от классического пироэлектрического эффекта, величина наблюдаемого термоотклика пропорциональна увеличению температуры кристалла и не зависит от скорости ее изменения. Формула для термоиндуцированного напряжения на сопротивлении нагрузки Rn выглядит в общем случае как
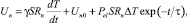(1)
где S – площадь поверхности кристалла, покрытой нанесенным электродом;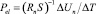 
– коэффициент, характеризующий величину термоЭДС в режиме измерения Un (А/К×м2); ΔUn – изменение напряжения на Rn при изменении температуры образца на ΔT; ΔT – разность начальной и конечной температур образца; Un0 – первоначальное напряжение при T0 (T0 – начальная температура кристалла); τ – время релаксации термоотклика; γ – пироэлектрический коэффициент; t – время. Первый член в (1) соответствует классическому пироэффекту, а второй описывает собственно неравновесный термовольтаический эффект, значительно выделяющийся из общего сигнала благодаря большому времени релаксации (τ ≥ 105 с). Изучение эффекта проводилось с помощью медленной модуляции температуры кристалла в условиях термостата, термоЭДС фиксировалась в том числе в стационарных условиях.
В экспериментах использовались беспримесные и легированные железом кристаллы НЛ с толщиной от 0,1 до 2 мм и площадью от 1 мм2 до 3 см2. Металлические электроды наносились напылением в вакууме (толщиной от 0,1 до 1 мкм).
Были исследованы образцы с различными парами электродов: алюминий (Al) – хром (Cr), индий (In) – хром (Cr), алюминий (Al) – аквадак (С), алюминий (Al) – медь (Cu), серебро (Ag) – алюминий (Al). Исходя из требований экономичности, износостойкости и максимально наблюдаемой величины термоотклика в основном использовались пары электродов: алюминий (Al) – хром (Cr), медь (Cu) – алюминий (Al).
Специальные измерения показали, что эффект термоотклика имеет примерно одинаковую величину в кристаллах как Y-, так и Z-срезов. Поскольку в установке применялись достаточно большие скорости нагрева [около 0,1 град. в с], то для кристаллов Z-среза пироток достигал значительной величины. Поэтому основные измерения проводились для кристаллов НЛ Y-среза, где можно наблюдать термоотклик в чистом виде. Однако полностью избавиться от пироэффекта не удается – даже для образцов Y-среза характерная зависимость напряжения Rн от t обнаруживает начальный выброс (в момент включения нагрева). Выброс, по-видимому, связан с неточным срезом кристалла, а также блочной структурой кристалла и, следовательно, является компонентой пиротока. Произведенные оценки дают величину отклонения от чистого Y-среза в 1–3°, что вполне реально.
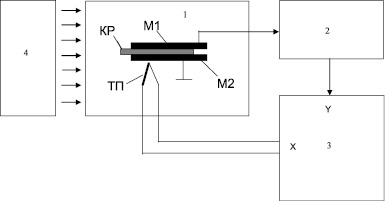
Рис. 1. Блок-схема экспериментальной установки: 1 – кристаллодержатель (КР – кристалл; М1, М2 – напыленные электроды из разных металлов; ТП – термопара); 2 – усилитель постоянного тока У5 – 9; 3 – графопостроитель Н 306; 4 – электрическая печь
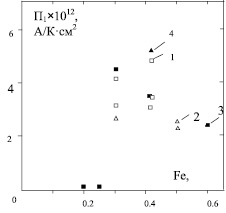
Рис. 2. Зависимость коэффициента П1 от концентрации примеси железа в кристалле НЛ для разных срезов и материалов контактов: 1 – Al–Cr, Z-cрез; 2 – In–Cr, Z-срез; 3 – Al–Cr, Y-срез; 4 – In–Cr, Y-срез
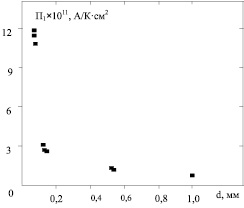
Рис. 3. Зависимость коэффициента П1 от толщины кристалла: S = 5 мм2; 0,3 вес. % Fe; Al – Cr
Для изучения зависимости величины термоотклика от концентрации примеси использовались кристаллы НЛ с одинаковыми площадью и толщиной [S = 0,5 см2, d = 1 мм]. Концентрация железа варьировалась в пределах от 1,3·10–2 до 0,7 вес. %.
Результаты представлены на рис. 2. Для концентрации примеси менее 0,25 вес. % эффект термоотклика не наблюдается.
Начиная с концентрации примеси 0,25 вес. %, коэффициент П1 резко возрастает и достигает максимума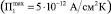 
при концентрации 0,3–0,4 вес.% Fe.
На этой же установке исследовалась зависимость величины коэффициента П1 от геометрии образца. Были получены следующие результаты: величина П1 резко возрастает с уменьшением толщины кристалла (рис. 3), П1 нелинейно зависит от площади образца (рис. 4).
При детальном изучении термоотклика было обнаружено, что П1 не является константой, а зависит от температуры образца, т.е. П1 = П1(ΔT) = J·Rн (рис. 5).
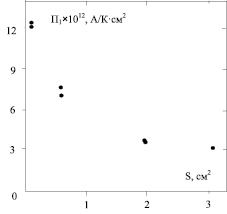
Рис. 4. Зависимость коэффициента П1 от площади кристалла (толщина кристаллов d = 1 мм; 0,3 вес. % Fe, электроды In–Cr, Z-срез, ΔT = 20 °C)
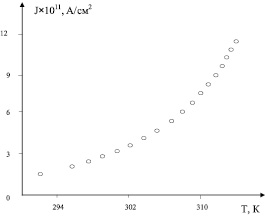
Рис. 5. Зависимость плотности тока от температуры кристалла (LiNbO3: Fe – 0,43 вес. %, 10×5×1 мм3; Y-срез; Al–Cr)
Измерения показали, что термовольтаический эффект имеет примерно одинаковую величину в кристаллах как Y-, так и Z-срезов. Поскольку в установке применялись достаточно большие скорости нагрева (около 0,1 К/с), то для кристаллов полярного Z-среза пироток достигал значительной величины. Поэтому основные измерения проводились для кристаллов ниобата лития Y-среза, где можно наблюдать термоотклик в чистом виде.
Металлические электроды наносились напылением в вакууме (толщиной от 0,1 до 1 мкм). Были исследованы образцы с различными парами электродов: алюминий – хром, индий – хром, алюминий – медь, серебро – алюминий.
Для изучения зависимости величины термоЭДС от концентрации примеси использовались кристаллы ниобата лития с одинаковыми площадью и толщиной (S = 0,5 см2, d = 1 мм). Концентрация железа варьировалась в пределах от 1,3·10–2 до 0,6 вес. %. Результаты представлены на рис. 1. Для концентрации примеси менее 0,25 вес. % термовольтаический эффект не наблюдается. Начиная с концентрации примеси 0,25 вес. %, коэффициент Pel резко возрастает и достигает максимума (Pel = 5·10–12 A/см2·К) при концентрации 0,3–0,4 вес. % Fe. Таким образом, из результатов исследования следует, что в тонкослойной системе металл – сегнетоэлектрик – металл термовольтаический отклик значительно возрастает при уменьшении толщины кристалла, что позволяет говорить о приконтактном механизме эффекта (связанном, например, с диффузией электродного металла в кристалл).
Известные контактные явления в сэндвичных структурах с сегнетоэлектриками не объясняют наблюдаемые квазистационарные токи [4, 5]. Наличие начального напряжения Un0 на образце позволяет говорить о неравновесной природе термостимулированного тока. При исследовании зависимости величины коэффициента Pel от геометрии образца было выявлено, что величина Pel резко возрастает с уменьшением толщины кристалла (рис. 2).
В данной работе предложена термохимическая модель исследуемого явления, обусловленного полем контактной разности потенциалов на границах раздела металл – сегнетоэлектрик. Предполагается, что появление тока вызвано появлением разности потенциалов в области контакта электрод – кристалл. В случае одинаковых материалов электродов контактные разности потенциалов равны и противоположно направлены. Тогда результирующая ЭДС равна нулю.
В аналогичном эксперименте из-за высоких электрических полей [более 103 В/см] наблюдалась окраска центров, подтверждая наличие электрохимических реакций в кристаллах. Модель предполагает, что электрохимическая окислительная реакция происходит в области контакта металл – сегнетоэлектрик, что приводит к появлению электрохимического потенциала.
Полученные результаты можно использовать для разработки приемников излучения [3–5], а также при интерпретации экспериментальных результатов по изучению свойств сэндвичных пироэлектрических структур [1, 2, 6, 9, 10].