Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

К аномальным, нетрадиционным коллекторам относятся залежи с низкими фильтрационными свойствами и пласты, содержащие высоковязкие нефти (ВВН). Запасы углеводородов в таких залежах, по разным источникам, весьма значительны. Извлечение углеводородов осложняется геологическими особенностями строения коллекторов, фильтрационно-емкостными свойствами, физическими свойствами нефти. Так, залежи высоковязкой нефти обладают достаточно высокой проницаемостью. Несмотря на это, движение флюидов в нетрадиционных коллекторах обладает общими свойствами – классический закон фильтрации Дарси не выполняется. Для низкопроницаемых коллекторов нарушается нижний предел применимости закона Дарси [6], для высокопроницаемых залежей ВВН основную роль в нарушении закона Дарси играет низкая подвижность флюидов. Для описания фильтрации флюидов вводится понятие начального градиента давления g, обобщенный закон фильтрации имеет вид:

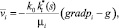(1)

где i = b, n соответствуют воде или нефти; k0 – абсолютная проницаемость; 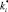– относительная проницаемость i фазы (ОФП); s – коэффициент водонасыщенности; μ_i – коэффициент динамической вязкости i фазы; gradpi – текущий градиент давления i фазы; g – начальный градиент давления. Фильтрация флюида наступает при условии превышения текущего градиента давления над начальным градиентом давления. В общем случае начальный градиент давления является функцией давления и температуры

g = g0f(Δp, ΔT), (2)

где Δp, ΔT – изменения пластовых давления и температуры соответственно; g0 – начальный градиент давления в пластовых условиях при Δp = ΔT = 0. Отметим, что зависимости g от давления изучены недостаточно. Зависимости g от ΔT приводятся в литературе, посвященной применению тепловых методов увеличения нефтеотдачи (МУН) в залежах ВВН. Поэтому для низкопроницаемых коллекторов, где тепловые МУН пока не используются, примем g = g0. Значения g0 определяются либо в лабораторных условиях, либо по данным интерпретации гидродинамических исследований скважин, причем результаты могут отличаться в десятки раз. Так, по результатам обработки гидродинамических исследований скважин Русского месторождения [7] интервал изменений от 0,021 до 0,45 1/МПа. На наш взгляд, результаты интерпретации гидродинамических исследований являются более достоверными. В работе [1] установлено, что начальный градиент давления обратно пропорционален корню квадратному из коэффициента абсолютной проницаемости 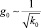, чем меньше проницаемость, тем больше начальный градиент давления. Следовательно, для низкопроницаемых пропластков, насыщенных маловязкими нефтями, на первый план выступают физические свойства коллектора. Для залежей ВВН g0 пропорционален вязкости нефти, для высокопроницаемых пропластков его величина в основном определяется составом и физическими свойствами нефти.

Рентабельный дебит обеспечивается путем создания в нетрадиционных коллекторах трещин – гидравлический разрыв пласта (ГРП) – и эксплуатации скважин с горизонтальным окончанием за счет создания гораздо большей площади фильтрации по сравнению с вертикальной или наклонной скважин, несмотря на малые скорости фильтрации.

Дебит скважины Q определяется как произведение скорости фильтрации v на площадь фильтрации S

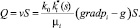(3)

Для горизонтальной части скважины площадь S = πdL, где d и L – диаметр и длина горизонтальной части ствола. Для ГРП величина S = 4s, где s – боковая площадь полутрещины.

При разработке нефтяных месторождений на естественных режимах с последующим воздействием на пласт посредством закачки холодной воды или теплоносителя вытеснение нефти зависит от характера продвижения фронта вытеснения от забоев нагнетательных скважин к добывающим. Процесс вытеснения нефти с применением теплоносителя в залежах с вязкопластичными нефтями рассмотрен в работах [5, 4].

В низкопроницаемых коллекторах вытеснение нефти будет происходить гораздо медленнее, нежели в коллекторах со средней или высокой проницаемостью. Это обусловлено нарушением классического закона Дарси. Поэтому, несмотря на то, что система ППД введена в работу, в начальный период эксплуатации добывающих скважин осуществляются естественные режимы разработки.

Для определения зоны, охваченной заводнением, построим уравнение пьезопроводности воды. Для этого используем уравнение движения (1) и уравнение неразрывности в виде

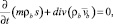(4)

где m – коэффициент открытой пористости; ρ_b – плотность закачиваемой воды, и реологическими уравнениями

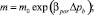
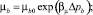
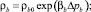
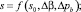
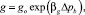(5)

где m0, μ_b0, ρ_b0, g0 – начальные значения коэффициентов пористости, вязкости воды, плотности и начального градиента; βpor, βb, βn, Δβ = βn – βb, βμ, βg – коэффициенты сжимаемости порового пространства, сжимаемости воды и нефти, изменения вязкости от давления, изменения начального градиента от давления соответственно; Δpb = pb – p0 – репрессия на пласт при закачке воды; pb – текущее давление закачиваемой воды; p0 – начальное пластовое давление; s0 – начальная, остаточная водонасыщенность.

Зависимость относительной фазовой проницаемости коллектора по воде 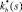от водонасыщенности определяется соотношением, построенным по результатам лабораторных исследований керна [2], зависимость коэффициента водонасыщенности s от давления (четвертое уравнение (5)) приведена в [7]. Используя результаты [2] и [3], получим зависимость ОФП по воде

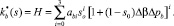(6)

Здесь abi – коэффициенты, определяемые обработкой результатов лабораторных исследований.

Подставив (1), (5), (6) в (4), получим уравнение пьезопроводности воды, которое в цилиндрических координатах имеет вид

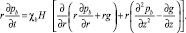(7)

Начало координат выбрано на забое нагнетательной скважины, ось z – нейтральная линия совпадает с серединой нефтенасыщенного пласта, h –толщина пласта от нейтральной линии (оси z) до кровли, коэффициент пьезопроводности воды

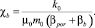
Отметим, что уравнение (7) справедливо не только для нетрадиционных, аномальных коллекторов, о которых шла речь выше, но и для коллекторов, в которых влиянием начального градиента давления g можно пренебречь. В отличие от плоскорадиальной фильтрации в (7) учитывается изменение давления по оси z, перпендикулярно напластованию.

Для определения радиуса фронта вытеснения нефти водой R(t) воспользуемся методом интегральных соотношений Г.И. Баренблатта. Краевые условия зададим следующим образом:

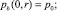
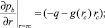
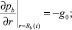
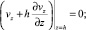
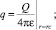
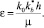(8)

К известным краевым условиям [4] следует добавить четвертое – граничное условие на кровле пласта, обусловленное непроницаемостью покрышки.

Давление в зоне заводнения определяется следующими соотношениями:

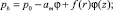
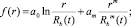
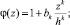
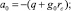
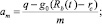
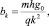(9)

где m, k – выбираются из сопоставления расчетных и промысловых данных.

Интегрируя уравнение (7) по r в интервале от rc до Rb(t) – фронта вытеснения нефти водой, получим дифференциальное уравнение для определения Rb(t):

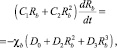(10)

где

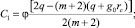
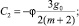
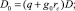
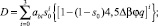
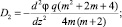
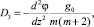(11)

где 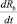– есть скорость продвижения фронта вытеснения. Параметр D учитывает зависимость ОФП коллектора по воде. При i = 0 D – const. Параметры D2 и D3 будут содержать слагаемые, зависящие от φ.

Рассмотрим два частных случая.

А) Плоскорадиальная фильтрация. φ = 1, D = 1, g0 = 0, D0 = q, C20 = 0, 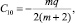D2 = D3 = 0. Интегрируя (10), получим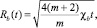 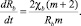При m = 1 первого соотношения получим формулу Баренблатта, 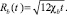Из второго соотношения следует, что скорость распространения фронта вытеснения убывает обратно пропорционально корню квадратному времени работы нагнетательной скважины.

Б) Пусть g0 = const, k = 1, m = 1, 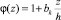– линейная функция переменной z, D = 0,29; 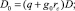D2 = D3 = 0, = 1. После интегрирования (10), получим кубическое уравнение

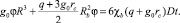(12)

Примем, что k0 = 5 мД = 5•10^–15 м2; g0 = 0,04 МПа/м; Qb = 18 м3/сут – приемистость, приходящаяся на верхнюю часть пласта толщина, которой равна h = 5 м; μ0 = 1 мПас; rc = 0,1 м; βpor = 6•10^–4 1/МПа; βb = 2•10^–4 1/МПа; βn = 10•10^–4 1/МПа; βμ = 0; βg = 0.

Поскольку φ является функцией z, то в отличие от плоскорадиальной фильтрации, значения радиуса фронта вытеснения на середине пласта и кровли будут разные. Зависимость Rb(t) по высоте пласта от нейтральной линии до кровли приведена на рисунке.

Из рисунка видно, что вытеснение нефти водой идет не равномерно, с ростом времени отставание фронта вытеснения на кровле (z = h) возрастает по сравнению с плоскорадиальной фильтрацией z = 0. Причем с продолжительностью времени закачки разница R(z = 0) – R(z = h) возрастает, и для t = 250 сут составляет около 50 м. Такая же картина наблюдается и для нижней части пласта –5 ≤ z ≤ 0. Это справедливо для изотропного по проницаемости пласта, в противном случае в уравнение (7) ко второму слагаемому правой части следует добавить сомножителем коэффициент анизотропии. Отметим, что если ОФП воды не учитывать, D = 1; то значение Rb(t) для тех же t будет больше. Так, для t = 100 сут Rb(t) = 276 м, а не 183 м, для t = 200 сут Rb(t) = 349 м, а не 231 м. Таким образом, на значение радиуса зоны вытеснения заметное влияние оказывает выбор коэффициента проницаемости. Если взять абсолютную проницаемость, то Rb(t) – радиус зоны вытеснения значительно больше, чем при учете фазовой проницаемости воды.

В качестве второго примера рассмотрим влияние величины начального градиента g0 на продвижение фронта вытеснения. Пусть g0 = 0; 0,05; 0,1 МПа/м.

Во втором столбце таблицы приведены значения Rb при g0 = 0 (случай А). Rb(t) пропорционален корню квадратному от времени. В столбцах третьем, четвертом и пятом приведены значения Rb(t) соответствующие рисунку. В трех последних столбцах приведены значения Rb(t) при g0 = 0,1 МПа/м. С увеличением начального градиента радиус зоны вытеснения уменьшается как на нейтральной линии, так и на кровле пласта. В зависимости от расположения добывающих скважин из рисунка или из таблицы определяется время начала обводнения продукции.

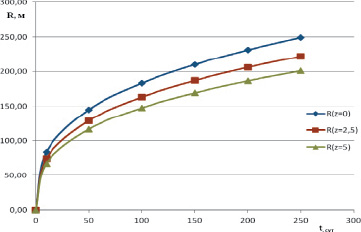
Зависимость фронта вытеснения Rb(t) от времени на нейтральной линии z = 0, z = 2,5 м, на кровле пласта z = 5 м

Зависимость фронта вытеснения Rb(t) от величины начального градиента g0

Если низкопроницаемый пласт состоит из нескольких прослоев с примерно одинаковой проницаемостью, то для расчетов их следует объединить в один с суммарной толщиной и средней по толщине проницаемостью. Если в пласте имеется высокопроницаемый прослой (ВП) с гораздо большей проницаемостью и гидродинамически связанный с низкопроницаемыми, то в этом случае следует учитывать переток флюида из низкопроницаемого пропластка (НП) в высокопроницаемый. Обводнение продукции будет проходить посредством преобладающей фильтрации воды по ВП, поэтому основная часть запасов нефти останется невыработанной, несмотря на высокую обводненность добываемой продукции.

Отметим, что для описания фильтрации нефти в зоне заводнения r_c ≤ r ≤ Rb(t) можно записать уравнение аналогичное (7), заменяя в параметрах индекс b на n, но q по-прежнему относится к закачиваемой воде. Другим способом определения характеристик фильтрации нефти в зоне совместной фильтрации служит хорошо известное соотношение

p_b – p_n = p_k,

где pk – капиллярное давление. Следует отметить, что капиллярное давление зависит от коэффициента водонасыщенности, который по мере удаления от забоя нагнетательной скважины, с одной стороны убывает, с другой, при постоянной приемистости увеличивается. Для расчета показателей добывающей нефтяной скважины, по аналогии с вышеизложенным, можно составить соответствующее уравнение пьезопроводности, а начало координат рекомендуется совместить с забоем добывающей скважины.

Таким образом, для описания вытеснения нефти из нетрадиционных коллекторов получено уравнение пьезопроводности воды, вытесняющей нефть с учетом изменения коэффициента водонасыщенности. Особенностью вытеснения флюидов является нарушение классического закона Дарси. При низкой проницаемости коллектора нарушен нижний предел его применения. Введение начального градиента давления, характеризующего фильтрационные особенности пласта и физические свойства нефти, позволяет определить радиус зоны вытеснения, следовательно, время начала обводнения добывающих скважин.