Оперативный контроль коллекторских характеристик прискважинной зоны позволяет оптимизировать процессы эксплуатации нефтяных и газовых месторождений и тем самым увеличивать продолжительность и эффективность эксплуатации нефтегазовых скважин [2–7]. Для исследования коллекторских характеристик призабойной зоны пластов используются различные гидродинамические, геофизические, термогидродинамические методы [8–11]. В данной работе для оценки коллекторских характеристик призабойной зоны пласта рассматривается метод опрессовки с введением газа. Этот метод можно применить для скоростного определения параметров в разведочных скважинах во время их бурения, а также в эксплуатационных скважинах в период их кратковременного отключения. В работе в качестве модельного примера рассматривается полость сферической формы.
Метод опрессовки заключается в следующем. В исходном состоянии давление газа во всем пористом пласте вокруг полости постоянно и равно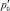 
, а сама полость заполнена газом. В начальный момент времени давление в полости мгновенно увеличивается до некоторого значения p0. За счет фильтрации газа в окружающую пористую среду значение давления внутри полости будет восстанавливаться. Темп релаксации давления в полости зависит от коллекторских характеристик окружающей пористой породы. Поэтому по времени релаксации давления можно оценить параметры породы вокруг полости, например величину коэффициента проницаемости.
Для оценки коллекторских характеристик пористой среды в работе предлагается использовать период полувосстановления давления в опрессованной полости. Периодом полувосстановления давления будем называть промежуток времени, в течение которого разница между значениями давлений в полости и пористой среде снижается в два раза от начальной разницы.
Основные уравнения
Пусть в исходном состоянии (t < 0) давление газа в пористой среде вокруг полости постоянно и равно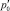 
, а сама полость заполнена газом. В момент времени t = 0 в полость дополнительно вводится газ и давление в ней мгновенно достигает значения p0. Далее за счет фильтрации газа в окружающее пористое пространство давление в полости стремится к значению 
.
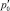При описании исследуемого процесса скелет пористой среды будем считать несжимаемым и однородным, а коэффициент вязкости газа – не зависящим от температуры и давления. В рамках вышеизложенных допущений, учитывая, что изменение массы газа в полости происходит только за счет его фильтрации через стенки полости в окружающую пористую среду, запишем уравнение сохранения массы газа в следующем виде [1, 4, 12]:
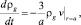(1)
где a – радиус полости; ρg – плотность газа; ν – скорость фильтрации газа через стенки полости.
Давление в окружающей полость пористой среде будем описывать с помощью нелинейного уравнения пьезопроводности:
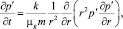a < r < ∞. (2)
Здесь μg – коэффициент динамической вязкости газа; p′ – давление газа вокруг полости; m и k – коэффициенты пористости и проницаемости окружающей полость пористой среды.
Учитывая, что в исходном состоянии давление газа во всем пористом пласте вокруг полости постоянно и равно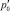 
, начальное условие для уравнения (2) запишем в виде
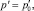t = 0, r > a. (3)
На стенке полости (r = a) выполняется условие непрерывности давления
p′ = p(t), t > 0, r = a, (4)
где p(t) – давление газа внутри полости.
Второе граничное условие уравнения пьезопроводности имеет вид
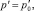t > 0, r → ∞. (5)
Аналитическое решение нелинейного уравнения пьезопроводности общего вида для фильтрации газа (2) при условиях (3)–(5) не найдено. В работе это уравнение будем использовать в линеаризованном приближении. Для этого перепишем уравнение (2) в линеаризованном виде:
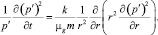(6)
Заметим, что изменение p′ мало относительно среднего значения этой величины, поэтому коэффициент при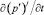 
в левой части уравнения (6) можно считать постоянным.
Таким образом, если во всей области течения и для всех значений t величина p′ мало отклоняется от своего начального значения, то уравнение (6) можно переписать в виде
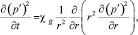(7)
где χg – коэффициент пьезопроводности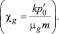 
Для описания фильтрации газа в пористой среде вокруг полости используем закон Дарси:
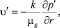(8)
где ν′ – скорость фильтрации газа вокруг полости. Используя условие неразрывности среды на стенке полости, для скорости фильтрации можно записать:
ν′ = ν (t > 0, r = a). (9)
Для замыкания системы уравнений (1), (7) и (8), считая, что газ является калорически совершенным, запишем уравнение, связывающее текущие значения плотности и давления в полости:
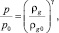(10)
где γ – показатель политропы; ρg0 – начальное значение плотности газа в полости.
Подставляя в уравнение (1) величину ρg из (10), получим
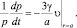(11)
Уравнение (11) связывает давление внутри полости со скоростью фильтрации газа через ее стенки.
Применяя принцип Дюамеля, решение уравнения (7), удовлетворяющее условиям (3–-(5), можем записать в виде
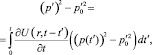(12)
где функция от двух переменных U(r, t) определяется по формуле
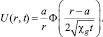(13)
Используя это решение, на основе уравнения (11) получим нелинейное интегральное уравнение
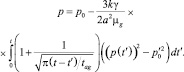(14)
Результаты численных расчетов
Нелинейное интегральное уравнение (14) было исследовано численным методом. Рис. 1 иллюстрирует влияние величины пористости m на процесс релаксации давления в полости. Тонкая горизонтальная штриховая линия на рис. 1, 2 пересекает графики зависимости безразмерного давления от времени в точках достижения периода полувосстановления давления. В расчетах использовались следующие значения параметров: γ = 1,4, a = 1 м,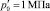 
. Видно, что период полувосстановления давления слабо зависит от коэффициента пористости.
На рис. 2 показано влияние коэффициента проницаемости пористой среды на процесс релаксации давления. Период полувосстановления давления обратно пропорционален коэффициенту проницаемости. При уменьшении коэффициента проницаемости в десять раз период полувосстановления давления увеличивается также в десять раз.
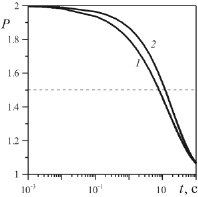
Рис. 1. Зависимости безразмерного давления от времени при различных значениях коэффициента пористости: 1 – m = 0,05; 2 – m = 0,2
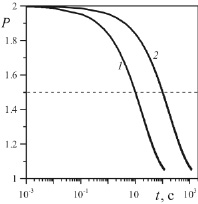
Рис. 2. Релаксация безразмерного давления при различных значениях коэффициента проницаемости: 1 – k = 10–13 м2; 2 – k = 10–14 м2
Зависимости периода полувосстановления давления от начального безразмерного давления в полости приведены на рис. 3. С увеличением значения начального безразмерного давления в полости период полувосстановления давления уменьшается. Это происходит из-за того, что чем больше значение перепада давления, тем больше скорость фильтрации газа через боковую поверхность полости при одинаковых остальных условиях. Поэтому при большем значении начального перепада давления происходит быстрое снижение давления в полости относительно его начального значения и тем самым быстрое достижение периода полувосстановления давления. В то же время следует отметить, что общее время релаксации давления в полости тем больше, чем больше значение начального перепада давления.
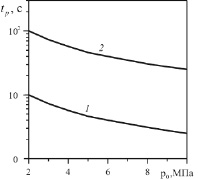
Рис. 3. Зависимости периода полувосстановления давления от значения начального безразмерного давления: 1 – k = 10–13 м2; 2 – k = 10–14 м2
Вывод
Предложенная методика и математическая модель, а также установленные зависимости периода полувосстановления давления в полости от коллекторских характеристик пористой среды могут быть использованы при определении параметров призабойной зоны газовых скважин и породы, окружающей газохранилище.