В 1805 г. Томас Юнг опубликовал работу, в которой установлена закономерность между краевым углом смачивания и поверхностными энергиями границ раздела фаз жидкость – газ, жидкость – твердое тело, твердое тело – газ [6]. В последующих исследованиях получено уравнение, связывающее краевой угол смачивания и поверхностные энергии контактирующих фаз. Таким образом, уравнение, обоснованное в трактате на тему о когезии жидкостей, получило в классических учебниках по физике, химии и в смежных областях наук (физическая, коллоидная химия) название закона Юнга:
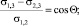 B = cosΘ.
B = cosΘ.
Здесь Θ, σ1,3, σ2,3, σ1,2 – краевой угол смачивания, °; поверхностные энергии границ раздела фаз твердое тело – газ, твердое тело – жидкость, жидкость – газ, Дж/м2; В – параметр, характеризующий смачивание.
Применение закона Юнга в прикладных исследованиях обусловлено относительной простотой измерения параметра, характеризующего смачивание, – краевого угла смачивания.
Теоретическая часть
Вывод закона Юнга на основе геометрического рассмотрения равновесия сил является нестрогим, поскольку соотношение между поверхностной энергией твердое тело – газ, твердое тело – жидкость и проекцией поверхностной энергии жидкость – газ не определяет полностью механического равновесия для капли жидкости, находящейся на поверхности твердого тела [4]. Иногда исследователи не принимают во внимание, что трехфазный периметр смачивания, который имеет сложное строение, определяет величину краевого угла смачивания и отличается по строению, энергетике взаимодействия жидкости с твердой фазой от остальной части жидкости, контактирующей с твердой фазой (рис. 1).
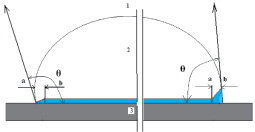
Рис. 1. Схема процесса смачивания, иллюстрирующая возможные отличия в строении области вблизи трехфазного периметра смачивания (ab) от остальной части жидкости, контактирующей с твердой фазой
Так, в работах А.И. Русанова показана возможность существования анизотропного краевого угла смачивания вследствие деформации анизотропного слоя поверхности [3]. Отмечено, что контактный угол не совпадает с краевым углом смачивания вследствие наличия работы деформации, которая может быть сведена к работе образования трехфазного периметра смачивания.
При проведении исследовательских работ величина краевого угла смачивания входит в уравнения методов измерения, имеющих достаточно высокую точность. Например, относительная точность измерений в капиллярном электрометре, предложенном Липпаном [9, 11], может достигать 0,01 %, но Лоуренс и Парсонс отметили, что в расчетах, возможно, присутствуют систематические ошибки вследствие того, что в уравнениях присутствуют параметры, связанные с краевым углом смачивания [10].
Появилось большое количество современных приборов, в которых с помощью ЭВМ контактный угол измеряют с абсолютной погрешностью ±0,1° [2]. В обзорах серии приборов DSA специалисты приводят методики расчета свободной энергии поверхности твердых тел (СЭП). Это известные модели Зисмана; Оунса, Вендта, Рабеля и Кабли (ОВРК); Фоукса; Ву [12, 14]:
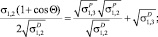
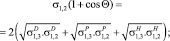
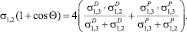
Здесь σP, σD σH – полярные, неполярные, компоненты энергии поверхности твердого тела, связанные с наличием водородных связей; Θ – краевой угол смачивания, град. Поверхности обозначены индексами в соответствии с рис. 1.
Основная часть
Рассмотрим возможность создания модели смачивания, основанной на нахождении параметров, которые достаточно просто измерить при исследовании системы, имеющей трехфазный периметр смачивания. Составим формальную схему смачивания сферической каплей жидкости твердой поверхности и определим изменение свободной энергии процесса ΔF (рис. 2).
Так как изменение свободной энергии процесса равно разности конечных и начальных состояний, получим уравнение для свободной энергии процесса:
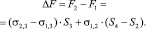 (1)
(1)
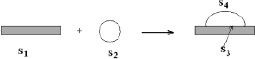
Рис. 2. Формальная схема процесса смачивания. S1, S2, S3, S4 – площадь твердой поверхности, жидкости, границы раздела фаз твердое тело – жидкость, жидкости после смачивания
В отличие от уравнения Юнга для характеристики процесса смачивания необходимо знание нескольких параметров, которые можно измерить в процессе эксперимента с высокой точностью. В данной модели гистерезисные явления в меньшей степени влияют на точность измерений, так как измерения проводят не краевых углов, а площади S2, S3, S4. Измерение касательных к кривым, которые сложно определить в точке трехфазного периметра смачивания, всегда являлось основным элементом, вызывающим дискуссию о достоверности результатов, количественных характеристик смачивания.
Если отнести изменение свободной энергии ΔF к начальной площади капли, уравнение (1) можно записать в форме двухпараметрической модели:
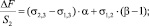
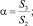
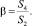 (2)
(2)
Для теоретического определения параметров α, β необходимо знать форму капли, лежащей на поверхности. В общем случае форма капли сложна и зависит от соотношения поверхностной и гравитационной энергии капли. Достаточно подробный анализ указанной проблемы выполнен в обзоре Р. Пейна [1], где даны ссылки на работы Гуи, Батлера, Башфорта, Адамса и других исследователей. Если поверхностная энергия много больше гравитационной энергии капли, лежащей на поверхности (для воды радиус капли должен составлять менее 0,5 мм), то форму капли можно интерполировать шаровым сегментом c радиусом наибольшей плоскости сечения равным R. Для указанной модели смачивания все параметры, равно как и все случаи смачивания, можно рассматривать как варианты сечения шара плоскостью. Используя условие равенства массы капли до и после смачивания, определим радиус кривизны R после смачивания:
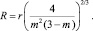 (3)
(3)
Здесь m – доля от радиуса при сечении шара плоскостью, начиная от вершины шара, m = 0…2; r – радиус капли до смачивания. Например, для условия cosΘ = 0 – это полусфера с радиусом R, равным 1,58740 r, (m = 1).
Площади соприкасающихся фаз S3, S4 как функции параметра m равны:
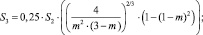
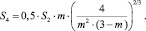 (4)
(4)
Приравнивая полный дифференциал уравнения (1) к нулю, получим параметрическое уравнение, характеризующее смачивание, как функцию параметра m:
 (5)
(5)
В качестве примера рассмотрим смачивание поверхности спектрального графита марки С-2 водой и 0,01 М раствором олеата калия (рис. 3).
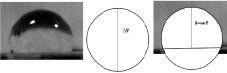
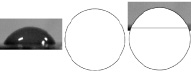
Рис. 3. Смачивание спектрального графита С-2 водой и 0,01 М раствором олеата калия
Так, радиус капли (r) до смачивания равен 4,80•10–4 м, что соответствует площади поверхности 2,895•10–6 м2. После смачивания поверхности графита водой площадь поверхности S3, S4 равна 0,850•10–6 м2; 2,338•10–66 м2, что соответствует параметрам: α = 0,294; β = 0,808. Для 0,01 М раствора олеата калия площадь поверхности S3, S4 равна 1,605•10–66 м2; 2,381•10–66 м2, что соответствует параметрам: α = 0,554; β = 0,822.
В действительности, при соблюдении определенных условий, нет необходимости измерять площади поверхности капли до и после смачивания. Достаточно определить параметр m и в соответствии с уравнением (5) провести расчет величины B′, характеризующей смачивание. Простота и удобство расчета заключается в том, что при интерполяции поверхности капли сферой можно выбрать любую систему координат, не связанную с истинными размерами капли. Так, в указанном примере при смачивании водой и раствором олеата натрия величина m равна 1,273; 0,6522, что соответствует величинам B’, равным –0,6553; –0,3203.
В приведенном примере расчетные величины краевых углов смачивания для системы вода – графит, раствор олеата калия – графит равны 98,08° (B = –0,1405); 79,49° (B = 0,1824). Сравнивая расчетные величины, характеризующие смачивание, по двухпараметрической модели (B′) и классической модели Юнга (B), отметим, что расхождения значительны.
В классической теории смачивания различают несколько вариантов, характеризующих процесс взаимодействия соприкасающихся фаз. Прежде всего, это условия полного смачивания и «абсолютно» гидрофобной поверхности, для которых cosΘ равны 1; –1. Подобные условия можно вывести для двухпараметрической модели – полного смачивания (m = 0) и «абсолютно» гидрофобной поверхности (m = 2):
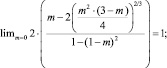
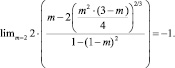
Несмотря на равенство граничных условий для полного смачивания и «абсолютно» гидрофобной поверхности, значения B, B′ на интервалах 1…–1 не совпадают (рис. 4). Так, по модели Юнга условная граница перехода от смачивания к несмачиванию в соответствии с величиной В равна нулю (Θ = 90°). По двухпараметрической модели указанная граница равна 61,68° (В′ = 0; m = 0,267). Сравним соотношения параметров смачивания по уравнению Юнга и предложенной модели смачивания (5) (рис. 4).
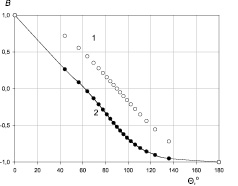
Рис. 4. Параметры смачивания (В′, В) по модели Юнга (1) и двухпараметрической модели (2) в зависимости от краевого угла смачивания
На графике представлены значения величин В, В′ в зависимости от величины краевого угла смачивания. В связи с выполненными расчетами остановимся на причинах в различии величин В, В′. Так, применение термодинамического метода Гиббса к расчету равновесия процесса смачивания предполагает соблюдение нескольких условий. Важное из них заключается в том, что система должна обладать конечными размерами для определения свободной энергии ΔF в начальных и конечных условиях. Например, при смачивании твердой поверхности каплей жидкости в виде эллипса и сферы свободная энергия ΔF будет различной – этот результат учитывает двухпараметрическая модель смачивания.
В классической теории смачивания для очень малых капель необходимо учитывать избыточную энергию периметра смачивания [5]. Если указанные энергии сопоставимы, например, в случае очень малых капель, радиусом менее 10–6 м, то целесообразно применять трехпараметрическую модель смачивания:
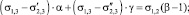
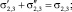
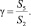
Здесь S5 – площадь трехфазного периметра смачивания область ab (рис. 1).
Трехпараметрическая модель смачивания может применяться в том случае, когда известны параметры области вблизи трехфазного периметра смачивания. Для количественных характеристик смачивания необходимо применять двух-, трехпараметрическую модель, учитывая, что современные методы исследований позволяют определять строение границы раздела вблизи трехфазного периметра смачивания [7, 8, 13].
Выводы
1. Предложена двухпараметрическая модель смачивания, основанная не на измерении краевых углов, а измерении параметров α, β, равных отношению площадей контактирующих фаз жидкости, твердого тела – жидкость к площади капли, наносимой на поверхность.
2. Двухпараметрическая модель смачивания основана на законах термодинамики и позволяет оценить процесс качественно и количественно. Гистерезисные явления в меньшей степени влияют на точность измерений, так как измерения проводят не краевых углов, а площадей контактирующих фаз.
3. Обосновано применение трехпараметрической модели смачивания, когда известны параметры и строение области вблизи трехфазного периметра смачивания.



