Формирование и эволюция вертикальной термодинамической структуры в модели экмановского пограничного слоя при интенсивном динамическом воздействии на исследуемую область среды может быть изучена при моделировании процессов, протекающих при шторме в верхнем слое океана (ВСО) в приближении его горизонтальной однородности [2, 4]. Использование такого допущения возможно, поскольку в большинстве случаев изменение основных термогидродинамических характеристик, вызванное взаимодействием океана с атмосферой при сильном ветре, будет по крайней мере на порядок больше, чем вызванное горизонтальной адвекцией и горизонтальным турбулентным обменом.
Для изучения внутрисуточной изменчивости ВСО при шторме будем исходить из следующей системы одномерных дифференциальных уравнений:
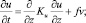 (1)
(1)
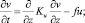 (2)
(2)
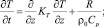 (3)
(3)
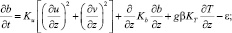 (4)
(4)
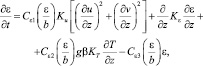 (5)
(5)
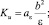
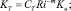
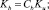
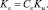 (6)
(6)
Источник тепла 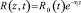 связан с объемным поглощением солнечной радиации в морской воде при коэффициенте ослабления η = 0,08 м–1; Ro – поток приходящей к поверхности океана солнечной радиации, расcчитанный с учетом отражения, поглощения и рассеяния в атмосфере. Параметр Кориолиса для умеренных широт f = 10–4 c–1;
связан с объемным поглощением солнечной радиации в морской воде при коэффициенте ослабления η = 0,08 м–1; Ro – поток приходящей к поверхности океана солнечной радиации, расcчитанный с учетом отражения, поглощения и рассеяния в атмосфере. Параметр Кориолиса для умеренных широт f = 10–4 c–1; 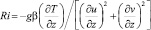 – градиентное число Ричардсона; β = 2•10–4 (°C)–1 – коэффициент термического расширения морской воды. Значения эмпирических констант подобраны из соображений согласованности с литературными источниками и наилучшего совпадения результатов расчетов с данными наблюдений. При вычислениях были использованы следующие коэффициенты: Cε1 = 3,0; Cε2 = 1,4; Cε3 = 3,2; Сb = 0,75; Cε = 1,0; aε = 0,08. Зависимость коэффициента KT от Ri [3] должна выполняться при различных физических процессах, протекающих в ВСО, подтверждаться достаточным объемом данных наблюдений и, кроме того, приводить к разумным результатам при решении задачи (1)–(5). Таким выражением может служить эмпирическая гипотеза Озмидова – Лозоватского (6) [4]. Соотношение получено для течений во внутренней области океана при 5•10–3 < Ri < 0,5 и турбулентных числах Рейнольдса (Ret = b2/(εν) не превышающих 104, где ν – кинематический коэффициент молекулярной вязкости). Применение этой формулы для случая слабой стратификации мало изучено. Поэтому в рамках данной модели был проведен ряд численных экспериментов, в которых варьировались значения констант ст и m. На основе анализа результатов проведенных расчетов для них установлены следующие значения: в период вовлечения ст = 1, m = 0 (KT = Ku); для всех остальных периодов ст = 0,03; m = 0,5.
– градиентное число Ричардсона; β = 2•10–4 (°C)–1 – коэффициент термического расширения морской воды. Значения эмпирических констант подобраны из соображений согласованности с литературными источниками и наилучшего совпадения результатов расчетов с данными наблюдений. При вычислениях были использованы следующие коэффициенты: Cε1 = 3,0; Cε2 = 1,4; Cε3 = 3,2; Сb = 0,75; Cε = 1,0; aε = 0,08. Зависимость коэффициента KT от Ri [3] должна выполняться при различных физических процессах, протекающих в ВСО, подтверждаться достаточным объемом данных наблюдений и, кроме того, приводить к разумным результатам при решении задачи (1)–(5). Таким выражением может служить эмпирическая гипотеза Озмидова – Лозоватского (6) [4]. Соотношение получено для течений во внутренней области океана при 5•10–3 < Ri < 0,5 и турбулентных числах Рейнольдса (Ret = b2/(εν) не превышающих 104, где ν – кинематический коэффициент молекулярной вязкости). Применение этой формулы для случая слабой стратификации мало изучено. Поэтому в рамках данной модели был проведен ряд численных экспериментов, в которых варьировались значения констант ст и m. На основе анализа результатов проведенных расчетов для них установлены следующие значения: в период вовлечения ст = 1, m = 0 (KT = Ku); для всех остальных периодов ст = 0,03; m = 0,5.
Краевые условия задачи (1)–(6) следующие:
z = 0: 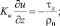
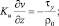
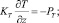
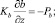
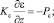
z = H: u = uH; v = vH;
T = TH; b = 0; ε = 0; (7)
t = 0: u = u0(z); v = v0(z);
T = T0(z); b = b0(z); ε = ε0(z).
Здесь τx, τy – составляющие касательного напряжения ветра на поверхности океана; PT – кинематический турбулентный поток тепла; 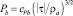 – поток энергии турбулентности (ρa = 1,29 кг•м–3 – плотность воздуха); Pε = 0 – поток скорости вязкой диссипации равен нулю ввиду недостатка эмпирических и теоретических сведений для его параметризации. Толщина верхнего слоя океана Н – это глубина, куда турбулентные возмущения с поверхности не достигают. Поэтому там скорость экмановского течения uH = vH = 0, а турбулентность вырождается b = 0; ε = 0.
– поток энергии турбулентности (ρa = 1,29 кг•м–3 – плотность воздуха); Pε = 0 – поток скорости вязкой диссипации равен нулю ввиду недостатка эмпирических и теоретических сведений для его параметризации. Толщина верхнего слоя океана Н – это глубина, куда турбулентные возмущения с поверхности не достигают. Поэтому там скорость экмановского течения uH = vH = 0, а турбулентность вырождается b = 0; ε = 0.
Задача (1)–(7) решалась численно конечно-разностными методами [1]. С целью повышения точности решения применялся итерационный метод последовательных приближений, суть которого заключается в использовании известных на момент решения задачи значений коэффициента вертикального турбулентного обмена импульсом с последовательным их уточнением на каждом временном шаге. По пространственной координате использовалась система сдвинутых сеток. При глубине расчетной области 50 м бралось от 500 до 1000 сеточных узлов. Временной шаг решения задачи равнялся 2 мин.
Модель была использована для воспроизведения развития вертикальной термодинамической структуры ВСО в период шторма, наблюдавшегося в районе станции погоды «Р» в Тихом океане 21–23 июня 1970 г. [5]. Потоки тепла, энергии турбулентности и составляющие касательного напряжения ветра на поверхности океана рассчитывались по известному дискретному временному ряду основных метеоэлементов (рис. 1) и серии вертикальных профилей температуры (рис. 2).
Отсутствие информации о начальном распределении составляющих вектора скорости течения, энергии турбулентности и скорости вязкой диссипации привело к необходимости первоначального нахождения стационарного решения системы уравнений (l)–(2), (4)–(5) без учета уравнения переноса тепла (3) при заданных постоянных потоках на поверхности океана, соответствующих скорости ветра W = 2 м/с (рис. 1) и первому температурному профилю (рис. 2).
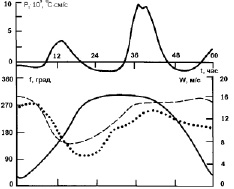
Рис. 1. Временной ход потока тепла (вверху) и изменения скорости (сплошная), направления (пунктирная) ветра и направления вектора скорости течения (точечная линия) на поверхности океана
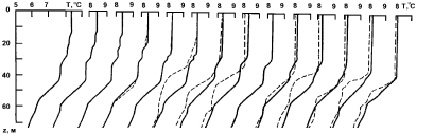
Рис. 2. Рассчитанные (сплошная линия) и наблюдаемые (пунктир) вертикальные профили температуры в период шторма с интервалом в 3 ч
Естественно, что такое приближенное задание начальных условий вносит определенные искажения в картину изменения вертикальной термодинамической структуры. Однако численные эксперименты показали, что небольшие вариации начальных условий прослеживаются в решении задачи лишь в течение короткого периода времени – от одного до нескольких часов, в зависимости от характера моделируемого процесса.
Рассматриваемый шторм длился 2 суток. Скорость ветра в течение первых 20 ч возросла до 16 м/с, затем сутки почти не менялась и вновь уменьшилась к исходному значению. Направление ветра претерпевало следующие изменения: юго-восточное (0 ч), западное (10 ч), северо-западное (16 ч), южное-юго-западное (все остальное время). К моменту установления максимального ветра скорость течения на горизонте 0,25 м возросла с 6,4 до 36 см/с (рис. 3). Для этого периода характерно аномальное изменение угла α (между направлениями векторов скорости течения и ветра), который определяется разностью значений пунктирной и точечной линий (рис. 1). Первоначально этот угол составлял 50° вправо от направления ветра, что не выходит за рамки оценок при обработке 2000 наблюдений дрейфа судов и хорошо согласуется с моделью эпюры скорости дрейфовых течений в тонком приповерхностном слое. Однако вследствие резкого разворота вектора скорости ветра вправо моделируемое течение не успевает адаптироваться и в какие-то моменты рассматриваемый угол меняется вплоть до 25° влево по ветру, что объясняется сильной нестационарностью в поведении динамических характеристик задачи.
Одновременно наблюдается быстрое увеличение составляющих u и v. Из-за разворота направления движения воды вправо вслед за ветром экмановская спираль вырождается в модель плиты и наблюдается как бы разгон течения, характеризующийся высокими скоростями по всему слою.
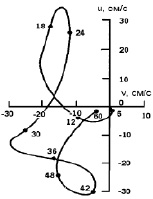
Рис. 3. Годограф вектора скорости течения на глубине 0,25 м, цифры у точек – время от начала шторма в часах
В период, когда ветер восстанавливает первоначальное направление движением против часовой стрелки, угол α принимает свое исходное значение, спираль Экмана четко выражена, скорость по слою заметно снижается и претерпевает колебания с инерционным периодом. На рис. 3 это выражается сложной эволюцией направления движения жидкости на горизонте 0,25 м. К моменту окончания шторма течение охватывает слой толщиной более 40 м и его скорость невысока.
Результаты расчетов показали в целом удовлетворительное количественное и качественное совпадение с данными наблюдений по температуре (рис. 2). Наибольшие расхождения приходятся на периоды ночной конвекции (1–3-й и 8–11-й профили). При этом рассчитанная температура оказалась завышенной на 0,2 °С, а глубина слоя, охваченного турбулентной конвекцией, получилась на 3–5 м меньше наблюдаемой. Однако, несмотря на такое несовпадение утренних профилей, модель достаточно быстро подстраивается под реальный процесс в соответствии с текущими значениями скорости ветра. К концу второго светового дня при одинаковой толщине изотермического слоя рассчитанная температура превышала наблюдаемую на 0,1 °С. Отмеченные недостатки, по-видимому, объясняются тем, что в задаче не учитывается адвекция тепла течениями, а также неточностью методики расчетов потока тепла при сильных ветрах.
Рис. 4–5 отражают результаты расчетов основных характеристик турбулентности. Можно заметить, что распределение энергии турбулентности по вертикали носит квазилинейный характер.
Для скорости вязкой диссипации (рис. 4), нормированной на 2ν, наблюдается быстрое квазиэкспоненциальное затухание с глубиной (при резко выраженном локальном максимуме в основании перемешанного слоя).
Наконец, для коэффициента турбулентной вязкости (рис. 5) характерно возрастание его значений в верхней части слоя ветрового перемешивания, а затем уменьшение (вплоть до значений, соответствующих турбулентному обмену в термоклине).
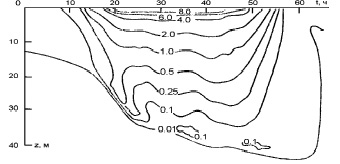
Рис. 4. Скорость вязкой диссипации, нормированная на 2ν
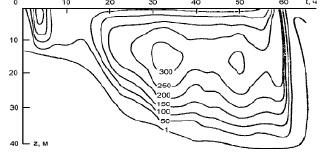
Рис. 5. Коэффициент турбулентной вязкости
Все динамические характеристики на поверхности океана сильно зависят от скорости ветра и в меньшей мере от потока тепла. Исключением является коэффициент вертикального турбулентного обмена импульсом, значение которого в периоды ночной конвекции почти на 20 % превосходит дневное. В изменении основных параметров мелкомасштабной турбулентности наблюдается некоторое запаздывание по сравнению с эволюцией внешних метеорологических факторов, которое на глубине 30 м составляет 2–3 ч. К моменту полного ослабления ветра в течение нескольких часов, слой, охваченный развитой турбулентностью, сужается от 40 до 5 м с сохранением изотермии.
Полученная эволюция основных гидрологических характеристик в период шторма качественно согласуется с современными представлениями, подтверждается наблюдениями и свидетельствует о способности использованной модели воспроизводить короткопериодную изменчивость верхнего слоя океана в период шторма.



