Весьма интересным и перспективным направлением развития альтернативной энергетики в последнее десятилетие принято считать использование в качестве электрогенераторов специфических микробов. В настоящее время ряд российских и зарубежных ученых занимаются исследованиями, связанными с разработкой новых и совершенствованием, имеющихся микробных топливных элементов (МТЭЛ) и публикуют весьма познавательные статьи, представляющие в позитивном свете получаемые в ходе проводимых экспериментов, результаты [1, 5]. Генерирование и использование возобновляемой биоэнергии рассматривается как одно из возможных направлений решения задачи обеспечения процессов рационального использования материальных и энергетических ресурсов. Основные направления работ в этой области посвящены развитию альтернативных методов производства электричества, в том числе с применением особых свойств микроорганизмов. Принципиальная возможность генерации электрического тока бактериями была доказана давно, уже почти сто лет назад, а устройства для генерации тока бактериями – микробиологические топливные элементы (МТЭЛы) достаточно интенсивно изучаются около пятидесяти лет. Технология, использующая микробные топливные ячейки, которые конвертируют энергию, запасенную в химических соединениях органического состава, в электрическую энергию, в результате жизнедеятельности микроорганизмов, продолжает вызывать у исследователей неподдельный интерес. Аналогичные исследования проводятся и в Калужском филиале МГТУ им. Н.Э. Баумана. На кафедре промышленной экологии и химии Калужского филиала МГТУ им. Н.Э. Баумана начиная с октября 2006 года проводятся фундаментальные исследования функционирования различных систем получения биоэнергии.
Основываясь на анализе особенностей этих систем, был осуществлен подбор оптимальных конструкционных материалов, необходимых для создания оригинальной биоэлектрической установки, а также экспериментально определены параметры биотехнологического процесса и отработаны его режимы, в том числе с использованием различных субстратов органического происхождения. Например, можно утверждать, что уже имеются и вполне обнадеживающие результаты исследований по осуществлению управляемой биодеградации отходов органического происхождения с одновременным получением электрической энергии, имеющие прикладное значение. В ходе совместных с ГНЦ РФ – ИМБП РАН работ было получено биоэлектричество из жидких органических отходов с использованием электрогенных бактерий (максимальные показатели DC получены с использованием микроорганизмов Shewanella oneidensis: напряжение – 0,48 В; сила тока – 200 мкА) [8, 9].
Однако проведение адекватного сравнения представляемых результатов затруднено ввиду отсутствия общепризнанных показателей унификации (хотя бы минимального обязательного набора ключевых характеристик), свидетельствующих о той, или иной степени технико-экономической эффективности МТЭЛ, которые можно использовать в качестве основы для, например, разработки новой конструкции МТЭЛ. Также, имеются данные о том, что некоторым сообществам различных штаммов электрогенных микроорганизмов свойственен определенный положительный синергизм – они обладают способностью более эффективно генерировать электричество, нежели отдельные штаммы [18].
Как следствие, если все эксперименты выполнять посредством одной лабораторной установки, подбор оптимальной загрузки для конкретного вида, например, содержащих органические отходы (субстраты) стоков, может растянуться на неопределенный срок, и в таком случае для ускорения исследований возникает необходимость приемлемой унификации, то есть требуется унифицировать алгоритм исследования.
Помимо финальных результатов эксперимента следует указывать максимальное количество исходных параметров:
– объем и тип питательного субстрата;
– объем и тип бактериальной загрузки;
– температуру проведения эксперимента;
– длительность эксперимента;
– площадь анода (если используется анод сложной формы, например, графитовая паста или графитовая ткань, то следует указывать эффективную площадь при пересчете на площадь стержней);
– площадь мембраны;
– электрические характеристики нагрузки.
Вероятно, в целях формирования оптимального перечня показателей унификации, нелишней будет также и прочая информация, свидетельствующая об особенностях конструкций лабораторных установок МТЭЛ, в том числе характеризующих применяемые способы обеспечения анаэробных условий, а также сведения о предпринятых мерах по проведению необходимой «адаптации» различных конструкций МТЭЛ, с целью обеспечения возможности беспрепятственного «снятия» и фиксирования вышеперечисленных параметров.
Другим немаловажным препятствием для унификации, вероятно, может быть различие периодов времени, необходимых для ферментации микроорганизмами, тех или иных видов органических отходов (субстратов).
Предположим, что в среднем срок одноразовой загрузки составляет около 7 суток и, следовательно, для проведения минимально необходимого числа повторных экспериментов (при безусловном устранении возможного влияния случайных факторов), для получения устойчивого среднего значения, измеряемых величин, удовлетворяющих условиям минимально приемлемой степени точности (общеизвестно, что при увеличении числа наблюдений оценка, практически любого параметра, будет стремиться к его истинному значению), что позволит выявить зависимости тех или иных, значимых характеристик МТЭЛ, потребуется не менее трех измерений, или 21 сутки работы одной лабораторной установки [7, 10, 11].
Напротив, зависимость мощности (напряжения и силы тока) МТЭЛ от конструктивных характеристик (объем загрузки, площадь мембраны, площадь анода, соотношение объема субстрата к объему бактерий) посчитать относительно несложно – достаточно провести серию экспериментов, изменяя по одному параметру несколько раз, а полученные значения свести в сравнительную таблицу.
Максимальную абсолютную погрешность этих измерений можно найти как сумму абсолютной инструментальной погрешности и абсолютной погрешности отсчета [6]:
Δх = Δхприб + Δхотсч.
После получения необходимых данных зависимость сводится в таблице, где одна характеристика представляет собой изменяемую конструктивную, а другая – полученную мощность (напряжение и сила тока). Проведение аппроксимации методом наименьших квадратов [3] позволит выявить искомую зависимость.
При проведении серии из n экспериментов с одной меняющейся характеристикой мы получим значения электрических характеристик (ток короткого замыкания и напряжение холостого хода) зависящих от изменяемой характеристики. Как следствие, мы сможем найти полином (n-1)-й степени, в точности выражающий результаты наблюдений для каждой характеристики.
Разумеется, все наблюдения сопряжены с неизбежными ошибками, и так как вполне естественно стремиться к наибольшей простоте эмпирических формул, то возникает задача об определении полинома m-ой, более низкой, чем число наблюдений без единицы, степени, выражающей данные наблюдений хотя и не точно, но с некоторой, по возможности минимальной, погрешностью. Подобная задача решается методом наименьших квадратов или Гаусса [2].
Пусть даны n значений независимого переменного x:
x1, x2, x3,…, xn
и соответственные им значения функций f(x):
f1, f2, f3,…, fn.
Требуется определить полином m-ой степени φ(x):
φ(x) = a0xm + a1xm–1 + a2xm–2 +…+ am–1x + am
обращающийся при x = xi в величину fi
Получаем, таким образом, ряд условий:
a0x1m + a1x1m–1 + a2x1m–2 +…+ am = f1
a0x2m + a1x2m–1 + a2x2m–2 +…+ am = f2
… … … … … … … … … … … … … … …
a0xnm + a1xnm–1 + a2xnm–2 +…+ am = fn.
Полученные n уравнений заключают (m + 1) неизвестных коэффициентов:
a0, a1, a2,…, am.
Поскольку число n, как правило, не равно (m + 1), то решение этой системы без дополнительных условий невозможно.
В таком случае φ(x) находят, например, методом наименьших квадратов: коэффициенты a0, a1, a2,…, am должны быть выбраны таким образом, чтобы сумма квадратов разностей φ(xi) – fi была наименьшей, т.е. чтобы была наименьшей сумма
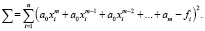
Для выполнения этого условия достаточно, чтобы:
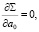
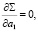
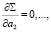
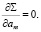
Это и даст (m + 1) линейных уравнений первого порядка с (m + 1) неизвестными:
a0, a1, a2,…, am.
Представленный пример математического моделирования относительно несложно реализовать посредством использования возможностей, предлагаемых пользователям в электронных таблицах MS Excel. Ведь к наиболее существенным достоинствам электронных таблиц следует отнести широкие возможности математического, статистического и графического анализа данных, эффективное моделирование проблем вида «что будет, если», прямой доступ к внешним базам данных, развитый интерфейс с другими популярными пакетами, поддержка средств мультимедиа, наличие инструментария для работы в сети Интернет. А при необходимости наличие в них встроенного языка программирования высокого уровня VBA сделает электронные таблицы еще более удобным легальным средством разработки приложений для научных и технических вычислений [15].
В случае необходимости, в целях унификации моделирования биотехнологических процессов, протекающих в МТЭЛ при использовании сообществ различных штаммов электрогенных микроорганизмов, которым, как отмечалось выше, свойственен определенный положительный синергизм, можно прибегнуть к уже имеющемуся опыту моделирования синергетических объектов с помощью облачных сервисов системы Mathematica [13, 14, 17].
Подводя итог, следует обратить внимание на то, что в общепринятом понимании термин «унификация» означает приведение к единообразию, к единой форме или системе. Многообразие же подходов к созданию МТЭЛ, а также различия в использовании исходной питательной среды и формирования условий протекания биотехнологических процессов, безусловно, подталкивают к созданию математических моделей, например, с использованием формализма нечеткой логики.
Для многих систем управления сложными технологическими процессами и объектами характерны неполнота и нечеткость информации, а также недостаточная надежность и степень формализации исходных данных (следует прикладывать все возможные усилия для того, чтобы формализовать упомянутую информацию для облегчения восприятия). При работе с такими объектами в последние десятилетия часто используется формализм нечеткой логики, подразумевающий, что для объекта моделирования должны быть определены входные и выходные переменные, а также их функции принадлежности, сформирована база знаний и проведены расчеты для типовых значений входных переменных. В качестве среды для программной реализации вычислительного алгоритма могут быть задействованы пакеты прикладных программ Matlab или Mathcad [4, 12, 13, 16].



